南方医科大学学报 ›› 2025, Vol. 45 ›› Issue (5): 1093-1102.doi: 10.12122/j.issn.1673-4254.2025.05.23
收稿日期:2024-11-26
出版日期:2025-05-20
发布日期:2025-05-23
通讯作者:
安胜利
E-mail:2895806365@qq.com;1069766473@qq.com
作者简介:梁芷玥,在读硕士研究生,E-mail: 2895806365@qq.com
基金资助:
Zhiyue LIANG( ), Lishan XU, Keke LI, Milai YU, Shengli AN(
), Lishan XU, Keke LI, Milai YU, Shengli AN( )
)
Received:2024-11-26
Online:2025-05-20
Published:2025-05-23
Contact:
Shengli AN
E-mail:2895806365@qq.com;1069766473@qq.com
摘要:
目的 通过比较临床试验中处理转组的常用方法,为不同场景下发生转组后分析方法的选择提供参考。 方法 基于肿瘤临床试验中患者转组的数据特征,分别模拟不同场景(样本量、患者预后、转组概率、治疗效果、膨胀因子)中患者的生存时间,比较意向治疗法(ITT)、符合方案法(PP)、删失法(PPcents)、实际治疗法(Treated)、秩保留结构加速失效模型(RPSFTM)、逆概率删失加权法(IPCW)、两阶段估计模型(TSE)、参数迭代法(IPE)所估计的治疗效应误差、均方误差与覆盖率。 结果 样本量对各方法的结果影响不大。相较于传统方法,复杂方法(RPSFTM、IPCW、TSE、IPE)在各种情况下误差均较低。IPCW法在转组概率较高时误差显著增加。TSE法在风险较低且转组概率较高时,误差和均方误差最低。IPE法在转组概率较低时具有明显优势,但在膨胀因子较小时可能会略低估治疗效应。 结论 转组概率较低且膨胀因子较小的情况下优先考虑IPE法或IPCW法;在转组概率较低且膨胀因子较大的情况下选择IPE法;在转组概率较大,膨胀因子较小且风险比较小的情况下选TSE法;其余情况建议选择RPSFTM法。
梁芷玥, 徐利珊, 李柯柯, 于米铼, 安胜利. 临床试验中不同转组分析方法的比较[J]. 南方医科大学学报, 2025, 45(5): 1093-1102.
Zhiyue LIANG, Lishan XU, Keke LI, Milai YU, Shengli AN. A comparative study of different methods for treatment switching analysis in clinical trials[J]. Journal of Southern Medical University, 2025, 45(5): 1093-1102.
| Variables | Assignment/Distribution |
|---|---|
| Simulation times | 1000 |
| Sample size | 200, 500, 1000 |
| Shape parameter | 0.5 |
| Scale parameter | 1.33 |
| observation time | 3 years |
| Survival time | Weibull distribution |
| Entry time | Uniform distribution (0-1distribution) |
| Prognostic probability (good/poor) | Good: 30%, 75% |
| Poor: 70%, 25% | |
| Switching probability (good, poor) | (0.1, 0.25) |
| (0.5, 0.75) | |
| Switching time | Uniform distribution |
| Hazard ratios | 0.7, 0.9 |
| Inflation factor | 1.2, 2 |
表1 模拟参数设置
Tab.1 Setting of the simulation parameters
| Variables | Assignment/Distribution |
|---|---|
| Simulation times | 1000 |
| Sample size | 200, 500, 1000 |
| Shape parameter | 0.5 |
| Scale parameter | 1.33 |
| observation time | 3 years |
| Survival time | Weibull distribution |
| Entry time | Uniform distribution (0-1distribution) |
| Prognostic probability (good/poor) | Good: 30%, 75% |
| Poor: 70%, 25% | |
| Switching probability (good, poor) | (0.1, 0.25) |
| (0.5, 0.75) | |
| Switching time | Uniform distribution |
| Hazard ratios | 0.7, 0.9 |
| Inflation factor | 1.2, 2 |
| Scenario | Hazard Ratios | Probability of good prognosis | Inflation factor | Switching probability (good : poor) | ||||
|---|---|---|---|---|---|---|---|---|
| 0.7 | 0.9 | 30% | 75% | 1.2 | 2 | 10%:25% | 50%:75% | |
| 1 | √ | √ | √ | √ | ||||
| 2 | √ | √ | √ | √ | ||||
| 3 | √ | √ | √ | √ | ||||
| 4 | √ | √ | √ | √ | ||||
| 5 | √ | √ | √ | √ | ||||
| 6 | √ | √ | √ | √ | ||||
| 7 | √ | √ | √ | √ | ||||
| 8 | √ | √ | √ | √ | ||||
| 9 | √ | √ | √ | √ | ||||
| 10 | √ | √ | √ | √ | ||||
| 11 | √ | √ | √ | √ | ||||
| 12 | √ | √ | √ | √ | ||||
| 13 | √ | √ | √ | √ | ||||
| 14 | √ | √ | √ | √ | ||||
| 15 | √ | √ | √ | √ | ||||
| 16 | √ | √ | √ | √ | ||||
表2 16 种场景下的参数值
Tab.2 Parameter values in 16 scenarios
| Scenario | Hazard Ratios | Probability of good prognosis | Inflation factor | Switching probability (good : poor) | ||||
|---|---|---|---|---|---|---|---|---|
| 0.7 | 0.9 | 30% | 75% | 1.2 | 2 | 10%:25% | 50%:75% | |
| 1 | √ | √ | √ | √ | ||||
| 2 | √ | √ | √ | √ | ||||
| 3 | √ | √ | √ | √ | ||||
| 4 | √ | √ | √ | √ | ||||
| 5 | √ | √ | √ | √ | ||||
| 6 | √ | √ | √ | √ | ||||
| 7 | √ | √ | √ | √ | ||||
| 8 | √ | √ | √ | √ | ||||
| 9 | √ | √ | √ | √ | ||||
| 10 | √ | √ | √ | √ | ||||
| 11 | √ | √ | √ | √ | ||||
| 12 | √ | √ | √ | √ | ||||
| 13 | √ | √ | √ | √ | ||||
| 14 | √ | √ | √ | √ | ||||
| 15 | √ | √ | √ | √ | ||||
| 16 | √ | √ | √ | √ | ||||
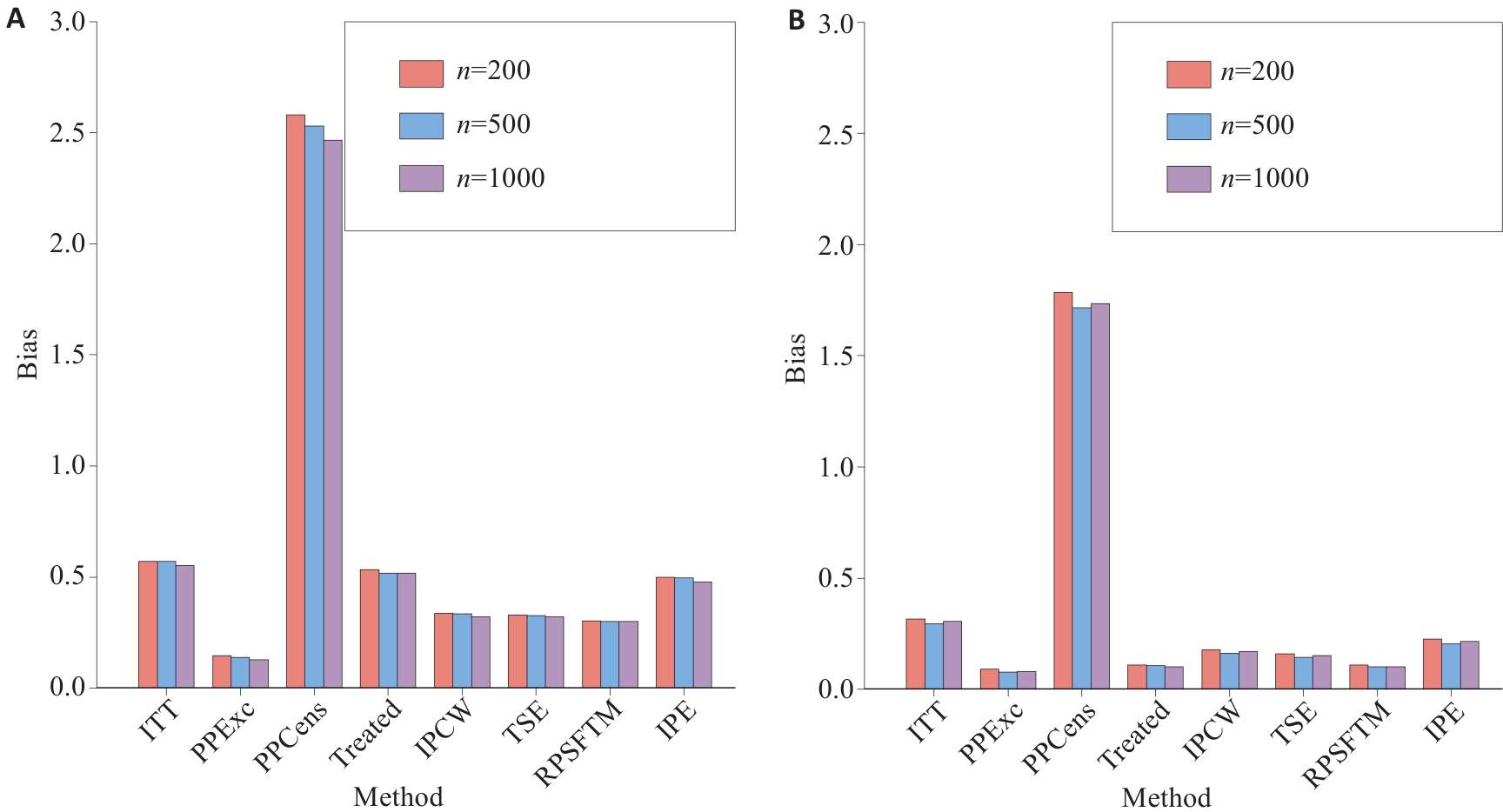
图2 场景4、14样本量比较结果
Fig.2 Impact of sample size on errors of different methods in Scenario 4 and Scenario 14. A: Scenario 4; B: Scenario 14. ITT: Intention-to-Treat; PPExc: Per-Protocol method; PPCens: Censoring Method; Treated: As-Treated Method; IPCW: Inverse Probability Censoring Weighting; TSE: Two-Stage Estimation; RPSFTM: Rank Preserving Structural Failure Time Models; IPE: Iterative Parameter Estimation Algorithm.
| Scenario | Method | Mean Estimate | Bias | MSE | SE | Coverage (%) |
|---|---|---|---|---|---|---|
Scenario6 beta=0.7 prob=0.75 a=1.2 prob1=(0.50, 0.75) | ITT | 0.98 | 0.28 | 0.09 | 0.11 | 95.2 |
| PPEXC | 0.76 | 0.06 | 0.02 | 0.11 | 94.9 | |
| PPCENS | 2.08 | 1.38 | 2.01 | 0.30 | 94.6 | |
| Treated | 0.92 | 0.22 | 0.06 | 0.11 | 95.9 | |
| IPCW | 0.85 | 0.15 | 0.03 | 0.10 | 95.2 | |
| Two-Stage | 0.84 | 0.14 | 0.03 | 0.10 | 95.2 | |
| RPSFTM | 0.98 | 0.28 | 0.08 | 0.05 | 99.4 | |
| IPE | 0.90 | 0.20 | 0.05 | 0.10 | 95.1 | |
Scenario7 beta=0.7 prob=0.75 a=2 prob1=(0.10, 0.25) | ITT | 0.98 | 0.28 | 0.09 | 0.11 | 95.4 |
| PPEXC | 0.93 | 0.23 | 0.06 | 0.11 | 94.3 | |
| PPCENS | 1.11 | 0.41 | 0.19 | 0.13 | 95.3 | |
| Treated | 1.09 | 0.39 | 0.17 | 0.13 | 94.3 | |
| IPCW | 0.94 | 0.24 | 0.07 | 0.11 | 95.4 | |
| Two-Stage | 0.94 | 0.24 | 0.07 | 0.11 | 95.3 | |
| RPSFTM | 0.96 | 0.26 | 0.08 | 0.07 | 98.8 | |
| IPE | 0.80 | 0.10 | 0.02 | 0.09 | 95.6 | |
Scenario14 beta=0.9 prob=0.75 a=1.2 prob1=(0.50, 0.75) | ITT | 1.20 | 0.30 | 0.10 | 0.13 | 95.5 |
| PPEXC | 0.98 | 0.08 | 0.02 | 0.13 | 94.9 | |
| PPCENS | 2.62 | 1.72 | 3.07 | 0.36 | 95.7 | |
| Treated | 1.01 | 0.11 | 0.02 | 0.11 | 95.8 | |
| IPCW | 1.06 | 0.16 | 0.04 | 0.11 | 94.8 | |
| Two-Stage | 1.04 | 0.14 | 0.03 | 0.11 | 94.6 | |
| RPSFTM | 1.00 | 0.10 | 0.01 | 0.01 | 100.0 | |
| IPE | 1.10 | 0.20 | 0.06 | 0.12 | 95.3 | |
Scenario15 beta=0.9 prob=0.75 a=2 prob1=(0.10, 0.25) | ITT | 1.24 | 0.34 | 0.13 | 0.14 | 95.3 |
| PPEXC | 1.19 | 0.29 | 0.10 | 0.14 | 95.1 | |
| PPCENS | 1.42 | 0.52 | 0.30 | 0.17 | 95.2 | |
| Treated | 1.23 | 0.33 | 0.13 | 0.13 | 95.0 | |
| IPCW | 1.20 | 0.30 | 0.11 | 0.13 | 94.9 | |
| Two-Stage | 1.20 | 0.30 | 0.11 | 0.13 | 95.3 | |
| RPSFTM | 1.14 | 0.24 | 0.07 | 0.12 | 97.8 | |
| IPE | 1.01 | 0.11 | 0.02 | 0.11 | 95.1 |
表3 不同风险比对各方法的影响
Tab.3 Impact of different hazard ratios on outcomes of different methods
| Scenario | Method | Mean Estimate | Bias | MSE | SE | Coverage (%) |
|---|---|---|---|---|---|---|
Scenario6 beta=0.7 prob=0.75 a=1.2 prob1=(0.50, 0.75) | ITT | 0.98 | 0.28 | 0.09 | 0.11 | 95.2 |
| PPEXC | 0.76 | 0.06 | 0.02 | 0.11 | 94.9 | |
| PPCENS | 2.08 | 1.38 | 2.01 | 0.30 | 94.6 | |
| Treated | 0.92 | 0.22 | 0.06 | 0.11 | 95.9 | |
| IPCW | 0.85 | 0.15 | 0.03 | 0.10 | 95.2 | |
| Two-Stage | 0.84 | 0.14 | 0.03 | 0.10 | 95.2 | |
| RPSFTM | 0.98 | 0.28 | 0.08 | 0.05 | 99.4 | |
| IPE | 0.90 | 0.20 | 0.05 | 0.10 | 95.1 | |
Scenario7 beta=0.7 prob=0.75 a=2 prob1=(0.10, 0.25) | ITT | 0.98 | 0.28 | 0.09 | 0.11 | 95.4 |
| PPEXC | 0.93 | 0.23 | 0.06 | 0.11 | 94.3 | |
| PPCENS | 1.11 | 0.41 | 0.19 | 0.13 | 95.3 | |
| Treated | 1.09 | 0.39 | 0.17 | 0.13 | 94.3 | |
| IPCW | 0.94 | 0.24 | 0.07 | 0.11 | 95.4 | |
| Two-Stage | 0.94 | 0.24 | 0.07 | 0.11 | 95.3 | |
| RPSFTM | 0.96 | 0.26 | 0.08 | 0.07 | 98.8 | |
| IPE | 0.80 | 0.10 | 0.02 | 0.09 | 95.6 | |
Scenario14 beta=0.9 prob=0.75 a=1.2 prob1=(0.50, 0.75) | ITT | 1.20 | 0.30 | 0.10 | 0.13 | 95.5 |
| PPEXC | 0.98 | 0.08 | 0.02 | 0.13 | 94.9 | |
| PPCENS | 2.62 | 1.72 | 3.07 | 0.36 | 95.7 | |
| Treated | 1.01 | 0.11 | 0.02 | 0.11 | 95.8 | |
| IPCW | 1.06 | 0.16 | 0.04 | 0.11 | 94.8 | |
| Two-Stage | 1.04 | 0.14 | 0.03 | 0.11 | 94.6 | |
| RPSFTM | 1.00 | 0.10 | 0.01 | 0.01 | 100.0 | |
| IPE | 1.10 | 0.20 | 0.06 | 0.12 | 95.3 | |
Scenario15 beta=0.9 prob=0.75 a=2 prob1=(0.10, 0.25) | ITT | 1.24 | 0.34 | 0.13 | 0.14 | 95.3 |
| PPEXC | 1.19 | 0.29 | 0.10 | 0.14 | 95.1 | |
| PPCENS | 1.42 | 0.52 | 0.30 | 0.17 | 95.2 | |
| Treated | 1.23 | 0.33 | 0.13 | 0.13 | 95.0 | |
| IPCW | 1.20 | 0.30 | 0.11 | 0.13 | 94.9 | |
| Two-Stage | 1.20 | 0.30 | 0.11 | 0.13 | 95.3 | |
| RPSFTM | 1.14 | 0.24 | 0.07 | 0.12 | 97.8 | |
| IPE | 1.01 | 0.11 | 0.02 | 0.11 | 95.1 |
| Scenario | Method | Mean Estimate | Bias | MSE | SE | Coverage (%) |
|---|---|---|---|---|---|---|
Scenario1 beta=0.7 prob=0.3 a=1.2 prob1= (0.10, 0.25) | ITT | 0.82 | 0.12 | 0.02 | 0.09 | 94.0 |
| PPEXC | 0.73 | 0.03 | 0.01 | 0.09 | 93.9 | |
| PPCENS | 0.99 | 0.29 | 0.10 | 0.12 | 93.8 | |
| Treated | 1.19 | 0.49 | 0.25 | 0.13 | 95.3 | |
| IPCW | 0.76 | 0.06 | 0.01 | 0.09 | 93.7 | |
| Two-Stage | 0.77 | 0.07 | 0.01 | 0.09 | 93.4 | |
| RPSFTM | 0.84 | 0.14 | 0.03 | 0.09 | 96.4 | |
| IPE | 0.68 | -0.02 | 0.01 | 0.08 | 93.6 | |
Scenario5 beta=0.7 prob=0.75 a=1.2 prob1=(0.10, 0.25) | ITT | 0.81 | 0.11 | 0.02 | 0.09 | 94.4 |
| PPEXC | 0.75 | 0.05 | 0.01 | 0.09 | 94.3 | |
| PPCENS | 0.92 | 0.22 | 0.06 | 0.11 | 94.3 | |
| Treated | 0.89 | 0.19 | 0.05 | 0.10 | 95.1 | |
| IPCW | 0.77 | 0.07 | 0.01 | 0.09 | 94.6 | |
| Two-Stage | 0.78 | 0.08 | 0.01 | 0.09 | 94.3 | |
| RPSFTM | 0.82 | 0.12 | 0.02 | 0.09 | 97.6 | |
| IPE | 0.66 | -0.04 | 0.01 | 0.07 | 94.9 |
表4 风险比较小时预后良好的概率对各方法的影响
Tab.4 Impact of the probability of "good" prognosis when the hazard ratio is low on outcomes of different methods
| Scenario | Method | Mean Estimate | Bias | MSE | SE | Coverage (%) |
|---|---|---|---|---|---|---|
Scenario1 beta=0.7 prob=0.3 a=1.2 prob1= (0.10, 0.25) | ITT | 0.82 | 0.12 | 0.02 | 0.09 | 94.0 |
| PPEXC | 0.73 | 0.03 | 0.01 | 0.09 | 93.9 | |
| PPCENS | 0.99 | 0.29 | 0.10 | 0.12 | 93.8 | |
| Treated | 1.19 | 0.49 | 0.25 | 0.13 | 95.3 | |
| IPCW | 0.76 | 0.06 | 0.01 | 0.09 | 93.7 | |
| Two-Stage | 0.77 | 0.07 | 0.01 | 0.09 | 93.4 | |
| RPSFTM | 0.84 | 0.14 | 0.03 | 0.09 | 96.4 | |
| IPE | 0.68 | -0.02 | 0.01 | 0.08 | 93.6 | |
Scenario5 beta=0.7 prob=0.75 a=1.2 prob1=(0.10, 0.25) | ITT | 0.81 | 0.11 | 0.02 | 0.09 | 94.4 |
| PPEXC | 0.75 | 0.05 | 0.01 | 0.09 | 94.3 | |
| PPCENS | 0.92 | 0.22 | 0.06 | 0.11 | 94.3 | |
| Treated | 0.89 | 0.19 | 0.05 | 0.10 | 95.1 | |
| IPCW | 0.77 | 0.07 | 0.01 | 0.09 | 94.6 | |
| Two-Stage | 0.78 | 0.08 | 0.01 | 0.09 | 94.3 | |
| RPSFTM | 0.82 | 0.12 | 0.02 | 0.09 | 97.6 | |
| IPE | 0.66 | -0.04 | 0.01 | 0.07 | 94.9 |
| Scenario | Method | Mean Estimate | Bias | MSE | SE | Coverage (%) |
|---|---|---|---|---|---|---|
Scenario9 beta=0.9 prob=0.3 a=1.2 prob1=(0.10, 0.25) | ITT | 1.02 | 0.12 | 0.03 | 0.11 | 95.0 |
| PPEXC | 0.93 | 0.03 | 0.01 | 0.10 | 95.7 | |
| PPCENS | 1.25 | 0.35 | 0.14 | 0.14 | 96.0 | |
| Treated | 1.10 | 0.2 | 0.05 | 0.12 | 95.9 | |
| IPCW | 0.97 | 0.07 | 0.01 | 0.10 | 95.0 | |
| Two-Stage | 0.97 | 0.07 | 0.01 | 0.10 | 95.5 | |
| RPSFTM | 0.99 | 0.09 | 0.01 | 0.05 | 99.7 | |
| IPE | 0.85 | -0.05 | 0.01 | 0.09 | 94.9 | |
Scenario13 beta=0.9 prob=0.75 a=1.2 prob1=(0.10, 0.25) | ITT | 1.02 | 0.12 | 0.03 | 0.11 | 94.8 |
| PPEXC | 0.97 | 0.07 | 0.02 | 0.11 | 95.1 | |
| PPCENS | 1.17 | 0.27 | 0.09 | 0.13 | 94.2 | |
| Treated | 1.02 | 0.12 | 0.02 | 0.11 | 94.6 | |
| IPCW | 0.99 | 0.09 | 0.02 | 0.11 | 95.0 | |
| Two-Stage | 0.99 | 0.09 | 0.02 | 0.11 | 94.9 | |
| RPSFTM | 1.00 | 0.10 | 0.01 | 0.07 | 98.6 | |
| IPE | 0.83 | -0.07 | 0.01 | 0.09 | 94.9 |
表5 风险比较大时预后良好的概率对各方法的影响
Tab.5 Impact of the probability of "good" prognosis with a high hazard ratio on outcomes of different methods
| Scenario | Method | Mean Estimate | Bias | MSE | SE | Coverage (%) |
|---|---|---|---|---|---|---|
Scenario9 beta=0.9 prob=0.3 a=1.2 prob1=(0.10, 0.25) | ITT | 1.02 | 0.12 | 0.03 | 0.11 | 95.0 |
| PPEXC | 0.93 | 0.03 | 0.01 | 0.10 | 95.7 | |
| PPCENS | 1.25 | 0.35 | 0.14 | 0.14 | 96.0 | |
| Treated | 1.10 | 0.2 | 0.05 | 0.12 | 95.9 | |
| IPCW | 0.97 | 0.07 | 0.01 | 0.10 | 95.0 | |
| Two-Stage | 0.97 | 0.07 | 0.01 | 0.10 | 95.5 | |
| RPSFTM | 0.99 | 0.09 | 0.01 | 0.05 | 99.7 | |
| IPE | 0.85 | -0.05 | 0.01 | 0.09 | 94.9 | |
Scenario13 beta=0.9 prob=0.75 a=1.2 prob1=(0.10, 0.25) | ITT | 1.02 | 0.12 | 0.03 | 0.11 | 94.8 |
| PPEXC | 0.97 | 0.07 | 0.02 | 0.11 | 95.1 | |
| PPCENS | 1.17 | 0.27 | 0.09 | 0.13 | 94.2 | |
| Treated | 1.02 | 0.12 | 0.02 | 0.11 | 94.6 | |
| IPCW | 0.99 | 0.09 | 0.02 | 0.11 | 95.0 | |
| Two-Stage | 0.99 | 0.09 | 0.02 | 0.11 | 94.9 | |
| RPSFTM | 1.00 | 0.10 | 0.01 | 0.07 | 98.6 | |
| IPE | 0.83 | -0.07 | 0.01 | 0.09 | 94.9 |
| Scenario | Hazard ratios | Prognostic probability (good) | Inflation factor | Switching probability (good, poor) | Method | ||||
|---|---|---|---|---|---|---|---|---|---|
| 0.7 | 0.9 | 30% | 75% | 1.2 | 2 | 10%∶25% | 50%∶75% | ||
| 1 | √ | √ | √ | √ | IPE/IPCW | ||||
| 2 | √ | √ | √ | √ | TSE | ||||
| 3 | √ | √ | √ | √ | IPE | ||||
| 4 | √ | √ | √ | √ | RPSFTM | ||||
| 5 | √ | √ | √ | √ | IPE/IPCW | ||||
| 6 | √ | √ | √ | √ | TSE | ||||
| 7 | √ | √ | √ | √ | IPE | ||||
| 8 | √ | √ | √ | √ | TSE | ||||
| 9 | √ | √ | √ | √ | IPE/IPCW | ||||
| 10 | √ | √ | √ | √ | RPSFTM | ||||
| 11 | √ | √ | √ | √ | IPE | ||||
| 12 | √ | √ | √ | √ | RPSFTM | ||||
| 13 | √ | √ | √ | √ | IPE/IPCW | ||||
| 14 | √ | √ | √ | √ | RPSFTM | ||||
| 15 | √ | √ | √ | √ | IPE | ||||
| 16 | √ | √ | √ | √ | RPSFTM | ||||
表6 不同场景下最佳方法选择
Tab.6 Best Method Selection Under Different Scenarios
| Scenario | Hazard ratios | Prognostic probability (good) | Inflation factor | Switching probability (good, poor) | Method | ||||
|---|---|---|---|---|---|---|---|---|---|
| 0.7 | 0.9 | 30% | 75% | 1.2 | 2 | 10%∶25% | 50%∶75% | ||
| 1 | √ | √ | √ | √ | IPE/IPCW | ||||
| 2 | √ | √ | √ | √ | TSE | ||||
| 3 | √ | √ | √ | √ | IPE | ||||
| 4 | √ | √ | √ | √ | RPSFTM | ||||
| 5 | √ | √ | √ | √ | IPE/IPCW | ||||
| 6 | √ | √ | √ | √ | TSE | ||||
| 7 | √ | √ | √ | √ | IPE | ||||
| 8 | √ | √ | √ | √ | TSE | ||||
| 9 | √ | √ | √ | √ | IPE/IPCW | ||||
| 10 | √ | √ | √ | √ | RPSFTM | ||||
| 11 | √ | √ | √ | √ | IPE | ||||
| 12 | √ | √ | √ | √ | RPSFTM | ||||
| 13 | √ | √ | √ | √ | IPE/IPCW | ||||
| 14 | √ | √ | √ | √ | RPSFTM | ||||
| 15 | √ | √ | √ | √ | IPE | ||||
| 16 | √ | √ | √ | √ | RPSFTM | ||||
| 1 | Harmonisation ICF. E9(R1) Statistical Principles for Clinical Trials: Addendum: Estimands and Sensitivity Analysis in Clinical Trials; International Council for Harmonisation; Draft Guidance for Industry; Availability[J]. Fed Regist, 2017, 82(209): 7-14. |
| 2 | Shih A, Hsu CY, Shyr Y. Power and sample size calculation for non-inferiority trials with treatment switching in intention-to-treat analysis comparing RMSTs.[J]. Research square, 2024. |
| 3 | Lejun D, ChihYuan H, Yu S. Power and sample sizes estimation in clinical trials with treatment switching in intention-to-treat analysis: a simulation study.[J]. BMC Med Res Methodol, 2023, 23(1): 49. |
| 4 | 吴文凯, 何 俏, 姚明宏, 等. 罕见事件场景下处理双向治疗转换方法的模拟研究[J]. 中华流行病学杂志, 2025, 46(2): 334-44. DOI: 10.3760/cma.j.cn112338-20240522-00295 |
| 5 | Latimer NR, Dewdney A, Campioni M. A cautionary tale: an evaluation of the performance of treatment switching adjustment methods in a real world case study[J]. BMC Med Res Methodol, 2024, 24(1): 17. |
| 6 | Morden JP, Lambert PC, Latimer N, et al. Assessing methods for dealing with treatment switching in randomised controlled trials: a simulation study[J]. BMC Med Res Methodol, 2011, 11: 4. |
| 7 | Latimer NR, Abrams KR, Lambert PC, et al. Assessing methods for dealing with treatment switching in clinical trials: a follow-up simulation study[J]. Stat Methods Med Res, 2018, 27(3): 765-84. |
| 8 | Xuan J, Isa SM, Latimer N, et al. Is inverse probability of censoring weighting a safer choice than per-protocol analysis in clinical trials?[J]. Stat Methods Med Res, 2024, 34(2): 1029045591. |
| 9 | 宋佳丽, 孙凤宇, 卢宇红, 等. MIPE在临床试验转组研究中的应用[J]. 中国卫生统计, 2021, 38(2): 193-7, 203. DOI: 10.3969/j.issn.1002-3674.2021.02.008 |
| 10 | EunJin A, Hyun K. Intention-to-treat versus as-treated versus per-protocol approaches to analysis.[J]. Korean J Anesthesiol, 2023, 76(6): 531-9. |
| 11 | Law MG, Kaldor JM. Author's Reply: Survival analysis of randomized clinical trials adjusted for patients who switch treatments by M. G. Law and J. M. Kaldor, Statistics in Medicine, 15, 2069-2076 (1996)[J]. Statist Med, 1997, 16(22): 2620-1. |
| 12 | Xuan J, Isa SM, Latimer N, et al. Is inverse probability of censoring weighting a safer choice than per-protocol analysis in clinical trials[J]? Stat Methods Med Res, 2024, 34(2): 1029045591. |
| 13 | Reck M, De TL, Paz-Ares L, et al. Treatment-switching adjustment of overall survival in CheckMate 227 part 1 evaluating first-line nivolumab plus ipilimumab versus chemotherapy for metastatic nonsmall cell lung cancer[J]. Clin Lung Cancer, 2024, 25(7): e362-8. |
| 14 | Robins JM, Hernán MA, Brumback B. Marginal structural models and causal inference in epidemiology[J]. Epidemiology, 2000, 11(5): 550-60. |
| 15 | 李玉森. 单向交叉设计生存资料数据IPCW分析方法比较研究[D]. 西安: 第四军医大学, 2013. |
| 16 | Gorrod HB, Isa SM, Xuan J, et al. Adjusting for switches to multiple treatments: Should switches be handled separately or combined?[J]. Stat Methods Med Res, 2025, 34(2): 1029056081. |
| 17 | 于全骥, 倪森淼, 杨 旻, 等. 两阶段估计法在肿瘤临床试验转组分析中的应用[J]. 中国临床药理学与治疗学, 2021, 26(4): 395-400. DOI: 10.12092/j.issn.1009-2501.2021.04.006 |
| 18 | Latimer NR, Abrams KR, Lambert PC, et al. Adjusting for treatment switching in randomised controlled trials - A simulation study and a simplified two-stage method[J]. Stat Methods Med Res, 2017, 26(2): 724-51. |
| 19 | Latimer NR, White IR, Abrams KR, et al. Causal inference for long-term survival in randomised trials with treatment switching: Should re-censoring be applied when estimating counterfactual survival times?[J]. Stat Methods Med Res, 2019, 28(8): 2475-93. |
| 20 | School Of Health And Related Research UOSS, MRC Clinical Trials Unit UCLL, Population Health Sciences BMSU, et al. Improved two-stage estimation to adjust for treatment switching in randomised trials: g-estimation to address time-dependent confounding[J]. Stat Methods Med Res, 2020, 29(10): 2900-18. |
| 21 | Jackson D, Ran D, Zhang F, et al. New methods for two-stage treatment switching estimation[J]. Pharm Stat, 2025, 24(1): e2462. |
| 22 | Robins JM, Tsiatis AA. Correcting for non-compliance in randomized trials using rank preserving structural failure time models[J]. Commun Stat Theory Meth, 1991, 20(8): 2609-31. |
| 23 | Sullivan TR, Latimer NR, Gray J, et al. Adjusting for Treatment Switching in Oncology Trials: A Systematic Review and Recommendations for Reporting[J]. Value Health, 2020, 23(3): 388-96. |
| 24 | Bell Gorrod H, Latimer NR, Damian D, et al. Assessing the long-term effectiveness of cladribine vs. placebo in the relapsing-remitting multiple sclerosis CLARITY randomized controlled trial and CLARITY extension using treatment switching adjustment methods[J]. Adv Ther, 2020, 37(1): 225-39. |
| 25 | Latimer NR, Abrams KR, Amonkar MM, et al. Adjusting for the confounding effects of treatment switching-the BREAK-3 trial: dabrafenib versus dacarbazine[J]. Oncologist, 2015, 20(7): 798-805. |
| 26 | Bender R, Augustin T, Blettner M. Generating survival times to simulate Cox proportional hazards models[J]. Stat Med, 2005, 24(11): 1713-23. |
| 27 | Walker AS, White IR, Babiker AG. Parametric randomization-based methods for correcting for treatment changes in the assessment of the causal effect of treatment[J]. Stat Med, 2004, 23(4): 571-90. |
| 28 | Collett D. Modelling survival data in medical research[M]. 3rd ed. Taylor and Francis, 2015: 204-219 |
| 29 | Burton A, Altman DG, Royston P, et al. The design of simulation studies in medical statistics[J]. Stat Med, 2006, 25(24): 4279-92. |
| 30 | Latimer NR. Treatment switching in oncology trials and the acceptability of adjustment methods[J]. Expert Rev Pharmacoecon Outcomes Res, 2015, 15(4): 561-4. |
| No related articles found! |
| 阅读次数 | ||||||
|
全文 |
|
|||||
|
摘要 |
|
|||||