前列腺癌是男性最常见的癌症类型，高居美国男性癌症死亡原因的第2位^[1]。治疗前列腺癌的主要手段之一就是放射治疗，分次外照射（EBRT）作为前列腺癌放疗的一种标准治疗方案，其目标是最大限度把放射剂量集中到病变区（靶区），杀死肿瘤细胞，同时使其周围正常组织和器官少受或者免受不必要的照射。有研究指出，提高靶区的放射剂量是提高前列腺癌局控率的有效手段^[2]。然而，高剂量照射可能引起危及器官（OAR）（如直肠、尿道、膀胱等）的放射毒性增加，发生并发症的风险上升^[3]。因此，有必要建立预测模型来评估前列腺癌放疗中正常组织的放射性毒性。

目前临床上常采用ICRU 89号报告^[4]所推荐的剂量体积参数D_0.1cc，D_1cc和D_2cc来评估OAR的放射毒性，其中D_0.1cc，D_1cc和D_2cc分别表示OAR受到最高剂量照射的0.1 cm³，1 cm³和2 cm³体积内的最小剂量值。但是，利用剂量体积参数D_0.1cc，D_1cc和D_2cc来评估OAR的放射毒性存在以下局限：第一、剂量体积参数仅是基于OAR的剂量体积直方图（DVH）计算得到，没有包含任何剂量空间分布信息；第二、没有考虑治疗分次间OAR的形变，导致其剂量体积参数被高估。OAR的剂量体积参数通过简单累加各分次的剂量体积参数值得到，各分次剂量体积参数则是基于OAR高剂量点在放疗期间是不变的^[5-6]这一最坏条件假设下计算得到的，但在实际中摆位误差、器官位移和变形等问题的存在导致各分次剂量体积参数估值过高，进而高估了总体的OAR剂量体积参数。OAR实际受照剂量的高估约束了靶区分次剂量的提高，导致治疗效果不理想。因此，正确估计OAR的放射毒性有助于改善前列腺癌的放疗效果。以直肠为例，许多临床研究表明^[7-10]，直肠的放射毒性与其局部剂量分布信息密切相关。因此，在预测模型中加入剂量空间分布信息是非常有必要的。

当前，已有研究人员在直肠放射毒性预测模型方面开展了相关研究。例如，为评估宫颈癌放疗中的直肠并发症，Zhen等^[11]提出了一种基于深度学习（VGG-16 ^[12]）的预测模型；将配准后得到的3D直肠累积受照剂量分布平面展开成2D的直肠表面剂量分布，并直接将该2D的剂量分布用于VGG-16网络的训练和预测，取得了较为精确的结果。而Chen等^[13]则采用机器学习方法来构建宫颈癌放疗直肠并发症的预测模型。采用SVM分析从3D直肠表面剂量分布提取的剂量体积特征，从2D剂量分布提取的剂量几何特征以及纹理特征，构建宫颈癌放疗直肠并发症预测模型，该模型的结果明显优于应用D_0.1cc, D_1cc和D_2cc预测的结果。然而，上述方法有以下缺陷：（1）模态特征单一。上述两种方法均只考虑直肠表面剂量分布，然而在实际中，剂量分布可能并不是唯一的影响因素，其他临床参数也可能会导致直肠并发症的产生^[14]，并且有研究结果显示，多模态特征融合技术，可以提高预测的准确度^[15]。（2）仅使用单个分类器。根据“没有免费的午餐”定理^[16-17]任何一种分类算法都有其适应性，而针对具体问题，如何选择一种最适合的分类器算法，目前仍然没有定论^[18-19]，此分类器是否最适合直肠毒性预测问题有待考察。

对此，本研究创新地提出一种基于多准则决策的权重分配策略来实现多模态特征及多分类器的融合，并利用融合后的新型预测模型来评估前列腺癌放疗中直肠预后情况，最后通过与单模态单分类器的预测模型以及采用其他融合方式的预测模型进行比较验证了所提出模型的有效性。

本研究回顾性地收集了44例前列腺癌放疗病人的数据，包括临床治疗参数、计划CT图像和放疗计划。患者均接受了外照射放疗（EBRT），并根据直肠毒性评分等级将44例病人划分为经放疗后直肠有无并发症两类，其中直肠毒性Grade 0-1为直肠无并发症（17例），而Grade≥2为直肠发生并发症（27例）。

本文创新地提出一种基于多准则决策的多模态特征及多分类器融合模型。该模型不仅融合了前列腺癌放疗中的临床参数特征及剂量学特征（DVPs和DGPs）两种模态特征，还融合了支持向量机（SVM）^[20]、决策树（DT）^[21]、K近邻（KNN）^[22]、随机森林（RF）^[23]和XGBoost ^[24]5种分类器的信息。如此，该模型能使不同模态的信息进行互补，同时规避了选择最适合分类器的过程。如图 1所示，本模型包含4个主要部分，分别是：特征提取、特征选择、分类器决策融合以及模态信息融合。其训练过程如下：（1）提取临床参数特征以及剂量学特征，其中剂量学特征包括从直肠3D剂量分布提取的剂量体积参数和从2D剂量分布提取的剂量几何参数；（2）将提取的临床参数特征与剂量学特征分别进行特征选择；（3）将选择好的临床参数特征和剂量学特征分别训练SVM、DT、KNN、RF和XGBoost 5种分类器；（4）利用基于多准则决策的方法为单个分类器和单个模态分配权重ω_m(m = 1, 2, …, 5)和${{{\hat{\omega }}}_{n}}(n=1, 2) $。模型的测试过程与训练过程类似，共有五个步骤：（1）对待预测的病人提取临床参数特征和剂量学特征；（2）选出训练过程中被选定的特征；（3）将选择后的特征输入到训练好的SVM、DT、KNN、RF和XGBoost模型中进行预测；（4）利用ω_m(m = 1, 2, …, 5)对单个分类器的决策进行融合；（5）利用${{{\hat{\omega }}}_{n}}(n=1, 2) $对多模态信息进行融合，并得到最后的预测结果。

图 1(Fig.1)

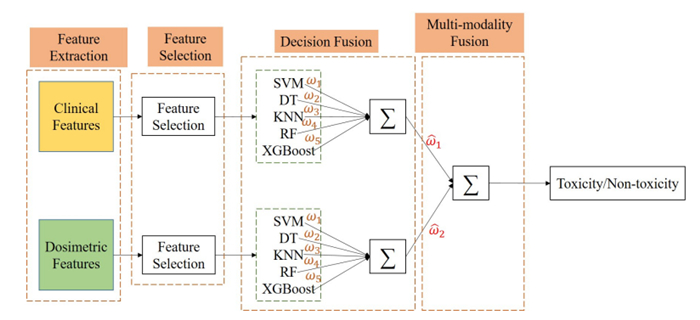
图 1 模型框架示意图 Fig.1 Framework of the proposed model.

从原始数据中提取的临床参数特征和剂量学特征如表 1所示。每一例病人的原始数据包括临床治疗参数、计划CT图像和放疗计划，其中临床治疗参数包含年龄、是否吸烟、是否患有糖尿病等18个特征。从计划CT图像和放疗计划中提取3D的直肠剂量分布并提取剂量体积参数（DVPs），即最高受照剂量体积x~cm³内的最小点剂量，其中x ∈[0.1, 2]，间隔为0.1 cm³，共20个剂量体积参数。按照文献[13、25]中的方法，将3D直肠剂量分布展开为2D的剂量分布，并提取剂量几何参数（DGPs），其定义为不同剂量水平下的剂量区域提取的几何特征，包括：相对面积、绝对面积、偏心率、周长等11大类共1100个特征。

表 1(Tab.1)

表 1 用于直肠并发症预测的临床特征和剂量学特征 Tab.1 Clinical parameters and dosimetric features used in rectal toxicity prediction Modalities Feature types Features Clinical Parameters (18) Demographic parameters (2) age; ethnicity Tumor characteristics (3) prostate-specific Antigen (PSA); gleason score; T-stage, phase Treatment parameters (6) biological equivalent dose; planning target volume (PTV); maximum length of PTV; maximum width of PTV; rectum volume prescription dose Rectum characteristics (2) rectal wall volume; ant rectum volume Other (5) smoking; diabetes; immunosuppression; history of colitis; prior hormonal therapy Dosimetric Features (1120) DVPs (20) D0.1 - cc~D2 - cc DGPs (1100) absolute area (mm2); relative area (%); eccentricity; major axis length (mm); minor axis length (mm); perimeter (mm); DBa; DLRb; DRRc; DTBd; DDBe aDB: Distance between centroid of the dose region and the bottom of the rectum (mm); bDLR: Distance between centroid and the leftmost of the rectum (mm); cDRR: Distance between centroid and the rightmost of the rectum (mm); dDTB: Distance between the topside of the dose region and the bottom of the rectum (mm); eDDB: Distance between the downmost and the bottom of the rectum (mm).

表 1 用于直肠并发症预测的临床特征和剂量学特征 Tab.1 Clinical parameters and dosimetric features used in rectal toxicity prediction

特征选择是在训练过程中，从原始特征集去除冗余特征，提取特征子集的过程。本研究采用LASSO回归^[26]的方法进行特征选择。LASSO回归是通过最小化$ \mathop {\min }\limits_{\bar w} \frac{1}{n}\sum\nolimits_{k = 1}^n {} {\left( {{y_k} - \bar w{x_k}} \right)^2} + \lambda \parallel \bar w{\parallel _1}$来求取一个系数向量$ \overline{w}\left(\overline{w} \in R^{d}\right)$，其中λ是一个控制系数向量稀疏程度的超参数，（其他的字母也要说明一下）。在得到的系数向量$ {\bar w}$中不为0的元素对应的特征即为被选中的特征。我们选择特征被选中频次较高的特征如表 2中所示，这些特征可能是预测前列腺癌放疗中直肠并发症的重要因素。

表 2(Tab.2)

表 2 经LASSO回归选择的高频次特征 Tab.2 High frequency features selected by LASSO Modality High frequency features Clinical parameters Age, Biological Equivalent Dose, PTV, rectal wall volume, ant rectum volume, rectum volume prescription dose, PSA, Ethnicity Dosimetric features D0.9 - cc, D1.0 - cc, D1.2 - cc, D2 - cc, Rel_area_16

表 2 经LASSO回归选择的高频次特征 Tab.2 High frequency features selected by LASSO

在测试过程中，模型首先在分类器层面上进行第一轮融合，然后在模态层面上进行第二轮的融合。因此，为单个分类器以及单模态分配权重是实现两轮融合的关键，对此，我们提出了一种基于多准则决策的权重分配算法来实现多模态特征和多分类器的融合。

本算法的思想是通过对不同评价指标的分析来为不同的评价对象分配权重。算法的具体流程如下：其输入是一个N×C的评价矩阵（N为评价对象的个数，代表多个分类器或者多个模态，C为评价指标的个数）以及评价指标的权重，经过正则化、权重化等步骤后计算每个评价对象的权重并归一化得到$ \hat{\omega}_{i}$。算法流程的伪代码如表 3所示，其中在本研究中选择的评价指标为准确性（Accuracy）、ROC曲线下的面积（AUC）、特异性（Specificity）和灵敏度（Sensitivity），评价指标的权重为α_j =1/M, j=1, 2, …, M。

表 3(Tab.3)

表 3 基于多准则决策的权重分配算法伪代码 Tab.3 Pseudocode of the proposed multi-criteria decision-making based weight allocation algorithm Multi-criteria decision-making based weight allocation algorithm Input:   A N × C evaluation matrix $ d_{i, j}(i=1, 2, \cdots, N, j=1, 2, \cdots, M)$ (N is the number of evaluation objects，represent for multi-calssifier and multi-modality，C is the number of evaluation criteria)；   The weights of evaluation criteria αj(j = 1, 2, …, M). Process： 1.Evaluation matrix normalization：   $ {{\tilde d}_{i, j}} = \frac{{{d_{i, j}}}}{{\sqrt {\sum\nolimits_{k = 1}^N {} d_{i, j}^2} }}i = 1, 2, \cdots , N, j = 1, 2, \cdots , M;$ 2.Evaluation matrix weighted by αj(j = 1, 2, …, M)：   ${{\hat d}_{i, j}} = {{\tilde d}_{i, j}} \times {\alpha _j}\;i = 1, 2, \cdots , N, j = 1, 2, \cdots , M; $ 3.Define the maximum and minimum under each evaluation criteria：   $ {\overrightarrow {EC} ^{\max }} = \left\{ {\max \left( {{{\hat d}_{i, j}}|i = 1, 2, \cdots , N} \right)|j = 1, 2, \cdots , M} \right\} \equiv \left\{ {ec_j^{\max }|j = 1, 2, \cdots , M} \right\}, $   ${\overrightarrow {EC} ^{\min }} = \left\{ {\min \left( {{{\hat d}_{i, j}}|i = 1, 2, \cdots , N} \right)|j = 1, 2, \cdots , M} \right\} \equiv \left\{ {ec_j^{\min }|j = 1, 2, \cdots , M} \right\}; $ 4.Calculating the distance of each evaluation object to the maximum and minimum：   $Di{s_{i, \max }} = \sqrt {\sum_{j = 1}^M {{{\left( {{{\hat d}_{i, j}} - ec_j^{\max }} \right)}^2}} } , i = 1, 2, \cdots , N, $   $ Di{s_{i, \min }} = \sqrt {\sum_{j = 1}^M {{{\left( {{{\hat d}_{i, j}} - ec_j^{\min }} \right)}^2}} } , i = 1, 2, \cdots , N;$ 5.Allocating weight for each evaluation object：   $ {\omega _i} = Di{s_{i, \min }}/\left( {Di{s_{i, \min }} + Di{s_{i, \max }}} \right);$ 6.Weight uniformization：   $ {{\hat \omega }_i} = \frac{{{\omega _i}}}{{\sum\limits_{k = 1}^N {{\omega _k}} }}, i = 1, 2, \cdots , N.$ Output: Weight for each evaluation object ${{\hat \omega }_i} = \left( {i = 1, 2, \cdots , N} \right). $

表 3 基于多准则决策的权重分配算法伪代码 Tab.3 Pseudocode of the proposed multi-criteria decision-making based weight allocation algorithm

利用基于多准则决策的权重分配算法确定好各分类器和各模态特征的权重后，我们下一步要实现分类器决策融合与模态信息融合。所谓分类器决策融合，是指对每个分类器的预测概率进行加权求和：$P^{m}=\sum\limits_{i=1}^{N} P_{i}^{m} \cdot \omega_{i}, i=1, 2, 3, m=1, 2 $，其中，P_i^m表示单模态下各个分类器对待预测样本的预测概率值，ω_i表示每个分类器的权重，P^m为当前模态下融合多分类器信息后的预测概率。而多模态信息融合过程则是对分类器决策融合的输出进行加权求和，如下式所示：$ P = \sum\limits_m {} {P^m} \cdot {{\hat \omega }_m}$，其中，（说明参数$ {P^m}$和${{\hat \omega }_m} $）。最终得到患者发生并发症的概率P和不发生并发症的概率（1-P）。

为了说明本文模型的有效性，我们在以下4个方面进行了实验：

（1）特征选择方法的验证

考虑到特征选择方法可能会对模型产生较大影响，本研究比较了了FCBF ^[27]，Trace_ratio ^[28]和reliefF ^[29]三种特征选择方法。

（2）基于多准则决策的权重分配算法的验证

为了说明基于多准则决策的权重分配算法的有效性，本研究将其与文献[30]所提到的三种分类器权重分配算法进行比较。与本研究所提出的权重分配算法不同，这些方法只根据分类器的准确率来计算权重，三种权重分配方法WF1、WF2和WF3，公式分别如（1）、（2）和（3）所示：

其中，η_n为分类器的准确率，${\eta _u} \buildrel \Delta \over = \max \left( {{\eta _n}} \right), {\eta _l} = \min \left( {{\eta _n}} \right) $。

（3）与单模态单分类器模型的比较

一方面，我们与单模态特征下各基分类器的表现进行比较；另一方面，我们还与单模态特征下决策融合后的模型进行比较。

（4）与不同融合模型的比较

为了说明完整模型的有效性，本研究与其他两种融合模型S1和S2进行了对比。图 2和图 3分别展示了S1和S2模型的融合过程。具体来说，S1模型直接对不同模态的特征进行融合（拼接），经过特征选择后再输入到RF和XGBoost两种集成分类器中；S2模型则是将两种模态特征分别输入到五种不同分类器（SVM、DT、KNN、RF和XGBoost）中进行训练，再对训练好的十个分类器进行决策融合。常用的决策融合方法包括多数投票法（PV）^[31]、常规加权融合方法（WAF）^[32]以及学习法（Stacking）^[33]，并在Stacking方法中采用采用逻辑回归^[34]作为次级学习器。

图 2(Fig.2)

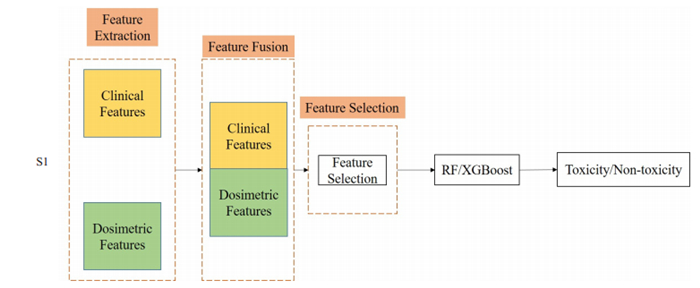
图 2 对比模型S1的融合示意图 Fig.2 Comparison reference ensemble scheme 1 (S1) to aggregate multi-modality features using Random Forests or XGBoost.

图 3(Fig.3)

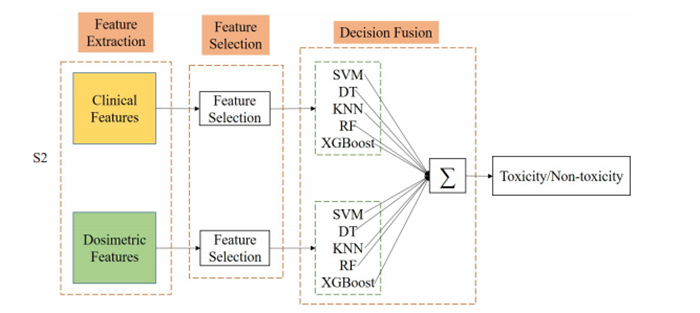
图 3 对比模型S2的融合示意图 Fig.3 Comparison reference ensemble scheme 2 (S2) to aggregate multi-modality features using PV, WAF or Stacking.

本研究采用五折交叉验证并重复五次的方法，对上述模型进行评估。评价指标包括ROC曲线、准确性（Accuracy）、ROC曲线下的面积（AUC）、特异性（Specificity）和灵敏度（Sensitivity），公式分别如下：

Accuracy=(TP+TN)/(TP+FP+FN+TN)

Specificity=TN/(TN+FP)

Sensitivity=TP/(TP+FN)，

其中，TP为真阳性，TN为真阴性，FP为假阳性，FN为假阴性。

与FCBF、Trace_ratio和reliefF三种不同的特征选择方法的结果对比如表 4所示，FCBF与LASSO有相近的预测结果，而Trace_ratio和reliefF算法的预测结果较差。

表 4(Tab.4)

表 4 不同特征选择方法的比较 Tab.4 Comparison of different feature selection methods Feature selection methods Accuracy AUC Specificity Sensitivity LASSO 0.78 0.83 0.79 0.76 FCBF 0.76 0.82 0.76 0.78 Trace_ratio 0.68 0.71 0.65 0.67 reliefF 0.65 0.68 0.59 0.62

表 4 不同特征选择方法的比较 Tab.4 Comparison of different feature selection methods

比较结果如表 5所示。不难发现，与文献[30]中提到的3种方法相比，本文所提出的基于多准则决策的分类器权重分配方法具有更高的Accuracy，AUC和Specificity。但也应注意，本方法在Sensitivity上表现较差。

表 5(Tab.5)

表 5 不同分类器权重分配算法的比较 Tab.5 Comparison of different weight allocation algorithms for classifiers Strategy Accuracy AUC Specificity Sensitivity The propose method 0.78 0.83 0.79 0.76 WF1 0.76 0.82 0.74 0.79 WF2 0.75 0.81 0.72 0.79 WF3 0.75 0.81 0.73 0.78

表 5 不同分类器权重分配算法的比较 Tab.5 Comparison of different weight allocation algorithms for classifiers

实验结果如表 6所示，其中列出了单模态特征下SVM、DT、KNN、RF和XGBoost 5种基分类器中表现最差和最好的分类器，同时也列出了这5种分类器决策融合后的结果作为对比，可以发现不同的分类器对数据的适应性是不同的，同时单模态下的决策融合取得的结果位于最差分类器与最优分类器之间，而本研究提出的模型在融合多模态与多分类器信息后在Accuracy、AUC、Specificity上都取得了最优的结果，其中Accuracy、AUC和Specificity分别为0.78、0.83和0.79，在Sensitivity上表现得稍差一些，只有0.76。

表 6(Tab.6)

表 6 本研究提出的模型与单模态单分类器结果比较 Tab.6 Comparison of the results by the proposed model and by the single modality single classifier Feature Accuracy AUC Specificity Sensitivity Clinical features   Best (SVM) 0.53 0.48 0.60 0.40   Worst (XGB) 0.73 0.75 0.67 0.83   Decision Fusion 0.67 0.70 0.73 0.57 Dosimetric features   Best (KNN) 0.73 0.80 0.68 0.82   Worst (DT) 0.69 0.68 0.69 0.68   Decision Fusion 0.70 0.81 0.69 0.71 The proposed model 0.78 0.83 0.79 0.76

表 6 本研究提出的模型与单模态单分类器结果比较 Tab.6 Comparison of the results by the proposed model and by the single modality single classifier

在本研究中，其结果如表 7以及图 4所示，可以发现，我们提出的融合模型较S1和S2两种融合模型在直肠并发症预测方面可以取得更准确得结果。

表 7(Tab.7)

表 7 本研究提出的模型与S1、S2的预测结果对比 Tab.7 Performance comparisons between the proposed model and S1, S2 Strategy Accuracy AUC Specificity Sensitivity S1   RF 0.66 0.71 0.63 0.71   XGBoost 0.70 0.78 0.73 0.66 S2   PV 0.69 0.80 0.73 0.62   WAF 0.69 0.79 0.71 0.67   Stacking 0.70 0.77 0.74 0.64 The proposed model 0.78 0.83 0.79 0.76

表 7 本研究提出的模型与S1、S2的预测结果对比 Tab.7 Performance comparisons between the proposed model and S1, S2

图 4(Fig.4)

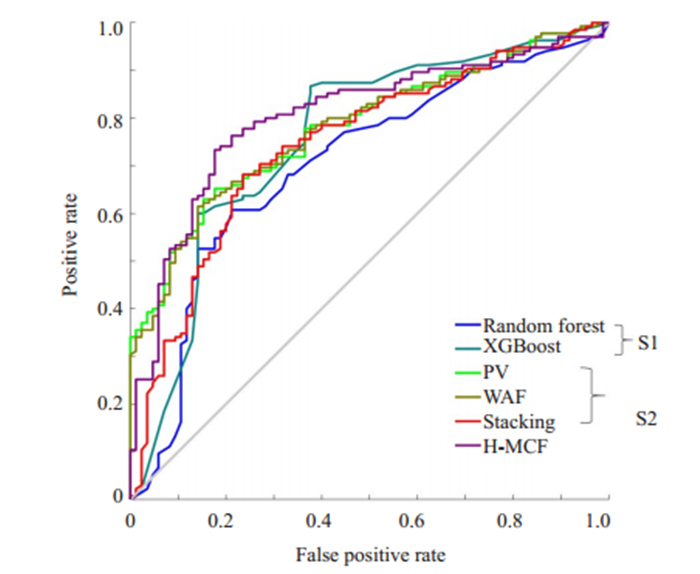
图 4 本研究提出的模型与S1、S2的ROC曲线 Fig.4 ROC analysis between H-MCF, S1, and S2.

在本研究中，我们创新地提出一种基于多准则决策的多模态特征及多分类器融合模型，并将其用于前列腺癌放疗直肠并发症的预测。该模型不仅考虑了临床和剂量两种模态特征，而且融合了多种分类器的信息。与其他融合模型相比，该模型能更准确地预测前列腺癌放疗中直肠并发症的存在。

对比FCBF、Trace_ratio和reliefF与LASSO方法选出的特征，我们发现FCBF方法选出的特征与表 2中选出的特征类似，而Trace_ratio和reliefF选出的特征则有较大差异，主要表现在剂量特征的选择上，Trace_ratio和reliefF在剂量特征中选出的特征主要是剂量几何参数下绝对面积这一项，与直肠并发症高度相关的剂量体积参数则一个都没有被选中。上述实验说明，特征选择方法也有其适应性，针对具体任务应具体分析。

在与不同权重分配算法的验证实验中，本研究所提出的基于多准则决策的分类器权重分配方法在准确率、AUC和特异性3个方面均表现最优，展现了本文方法的有效性，这可能是因为本研究提出的权重分配方法不仅仅依赖于分类器的准确率，而且还考虑了分类器其他的固有属性（如AUC、灵敏度等）。

从与单模态单分类器的结果中我们发现，不同分类器的适用范围不同。例如，复杂的XGBoost分类器在临床特征中表现最好，而在剂量学特征中表现最好却是简单的KNN，这再次证明“没有免费的午餐”定理^[16-17]。比较结果还表明，对多个基于单模态特征的分类器进行决策融合，虽然规避了最优单分类器的选择过程，但并不能保证模型始终得到最好的结果。相比之下，本研究所提出的融合模型始终好于各分类器以及各分类器融合，说明多模态特征融合能够提高模型预测的准确度，这一点与文献[15]是一致的。

与不同融合模型S1和S2相比，本研究提出的这种分层次的融合策略取得了更好的预测效果，其原因是它能够对多模态特征和多分类器进行更合理的管理。模型S1虽然利用了来自于不同模态的特征，但这些特征对模型的贡献是相同的，这是不合理的。因此我们需要一个特定的特征加权过程来突出那些对预测结果贡献更大的特征同时弱化那些无益的甚至对预测结果有反作用的特征。而对于模型S2而言，虽然每一种模态的特征都是被单独处理的，但是同时对不同模态下的多个分类器进行决策融合会使得某些适应性很差的分类器直接作用于最终的预测结果，进而导致预测失效。本研究所提出的分层融合方式能很好地改进模型S1和S2的不足，对多模态特征以及多分类器的权重分配也更合理。因此，本文模型取得更好的预测表现是符合预期的。

虽然本研究所提出的模型在前列腺癌放疗直肠并发症预测方面更具有竞争力，但是也存在一些缺陷。首先，未考虑多分类问题。基于多准则决策的权重分配算法在二分类问题下所使用的评价指标并不完全适用于多分类情况。其次，评价指标的分配也只是采用简单的平均法。因此，将本模型拓展到多分类问题上是我们未来的研究方向此外，还需要更多数据来进一步训练、验证和完善本研究所提出的模型。

本研究创新地提出一种基于多准则决策的权重分配算法来实现不同模态特征和多种分类器的分层融合，并在此基础上提出了一种基于多模态及多分类器融合的预测模型来估计前列腺癌放疗中直肠并发症的预后。与单模态单分类器以及其他融合模型相比，本研究所提出的融合模型能够更精准地预测直肠在前列腺癌放疗中的毒性，为未来有效安全地提高靶区剂量和前列腺癌局控率奠定基础。