颌骨囊肿是颌骨的常见良性病变，由于无自觉症状，常造成颌骨较多的吸收^[1-2]。从囊肿的病变范围考虑，直径在3.5 cm以上的囊肿一般不宜采取一次手术治疗方案^[3]，原因在于囊肿较大可致皮质骨吸收变薄，易导致病理性骨折；也不能够排除刮治术后由于应力集中而导致术区发生骨折，故针对大型颌骨囊肿多采用一期开窗减压术联合二期刮治术^[4-5]，既可减少病理性骨折的发生和重要解剖结构的损伤，又保存了患者的颌骨形态和功能^[6-7]，然而手术方式的选择多依据术者的临床经验，客观参考指标较少。相关报道^[8]仅模拟了下颌第三磨牙区不同程度骨吸收类型，对于颌骨不同部位囊性病变区的生物力学研究未见报道，因此本研究对下颌体部囊性病变模型行生物力学分析，并对囊肿大小及临界骨量进行了准确评估，预测由颌骨囊性病变导致颌骨骨折的可能风险，以期为临床选择手术方案提供参考依据。

三维有限元法是医学生物力学研究的重要方法，近年来被广泛应用于口腔生物力学研究领域^[9-11]，应用该方法可对牙齿、颌骨、牙周组织建立数学力学模型，反复进行各种约束、加载条件下的计算^[12-13]。因此为了评估下颌骨囊性病变大小对颌骨强度的影响，本研究以牙颌系统正常的健康成年女性志愿者下颌骨计算机螺旋CT扫描影像为基础，运用有限元分析（FEA）构建出单侧下颌体部囊性病变的三维有限元模型，分析在一定约束及载荷条件下病变区达到应力峰值时囊肿大小及剩余骨壁情况，为临床制定手术方案和应用FEA对颌骨囊肿的进一步研究打下基础。

选用牙列完整、咬合关系正常、颌骨发育正常无外伤史、无任何颞下颌关节紊乱症状和体征的成年女性健康志愿者1例作为建模素材。

以下颌骨Kelly分类^[14]方法为基础，囊性病变根据部位不同分为：Ⅰ类位于双侧颏孔之间称为正中联合部囊性病变；Ⅱ类位于颏孔至下颌第2磨牙远中面之间则为下颌体部囊性病变：Ⅲ类位于下颌第2磨牙远中面与升支部之间称为下颌角区囊性病变；Ⅳ类位于升支部至乙状切迹下方部位称为下颌升支区域囊性病变。本次研究针对的是Ⅱ类病变。

采用64排螺旋CT行下颌骨扫描，以此获取患者的影像学资料，以DICOM格式保存。

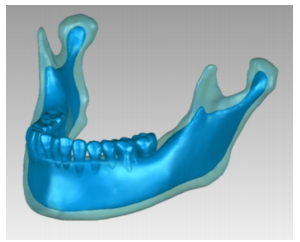
建立将CT扫描图像文件导入Mimics19.0软件中，进行阈值分割，图像分离后生成下颌骨3D模型，以STL格式导入Geomagic Studio2013软件，对下颌骨表面进行光滑处理，逆向成实体模型，再以STP格式导入SolidWorks2017软件中，模拟出下颌体部囊性病变模型，最后导入ANSYS Workbench17.0软件中建立单侧下颌体部囊性病变三维有限元模型（图 1~3）。

图 1(Fig.1)

图 1 下颌骨实体模型 Fig.1 Mandible solid model

图 2(Fig.2)

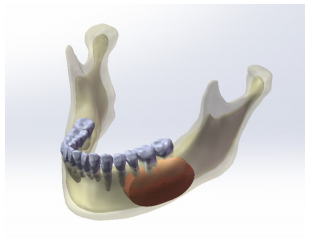
图 2 下颌体部囊肿模型 Fig.2 Mandibular body cyst model

图 3(Fig.3)

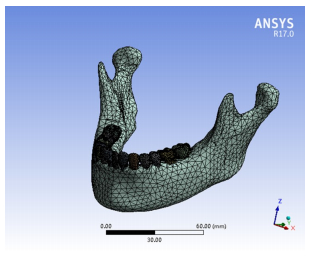
图 3 下颌骨囊性病变三维有限元模型 Fig.3 Three-dimensional finite element model of mandibular cystic lesion

假设模型中皮质骨与松质骨材料性质连续、均质、各向同性，牙齿设为各向同性^[15-16]。松质骨屈服强度定义为13Mpa，密质骨屈服强度定义为83.2 Mpa^[17]。具体材料参数^[18-20]详见表 1。

表 1(Tab.1)

表 1 材料相关参数 Tab.1 Parameters of the cortical bone, cancellous bone and teeth in the 3D finite element model Material Elastic modulus (MPa) Poisson's ratio The yield strength (MPa) Cortical bone 1.37×104 0.3 83.2 Cancellous bone 1.37×103 0.3 13 Teeth 1.86×104 0.31 - a: Elastic modulus: in the elastic deformation stage of materials, their stress and strain should be proportional to each other, and the proportional coefficient is called elastic modulus; b: Poisson's ratio: when the material is stretched or compressed, the material will deform. The ratio of transverse deformation to longitudinal deformation is poisson's ratio, which is a dimensionless physical quantity

表 1 材料相关参数 Tab.1 Parameters of the cortical bone, cancellous bone and teeth in the 3D finite element model

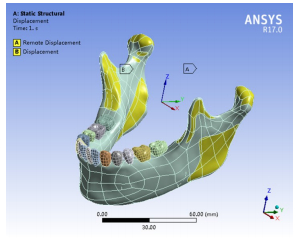
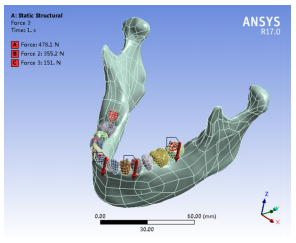
（1）位移边界条件：将髁突顶部约束为铰链，三维方向都固定约束，双侧髁突固定，使之不能移动，只能转动；咬肌、颞肌、翼内肌以及翼外肌附着处单元进行0位移约束（图 4）。（2）载荷边界条件：下颌切牙切缘、双侧第1前磨牙牙合面、双侧第1磨牙牙合面加载咬合力分别为151 N、355.2 N、478.1 N^[21]（图 5）。

图 4(Fig.4)

图 4 位移边界条件 Fig.4 Displacement boundary conditions

图 5(Fig.5)

图 5 载荷边界条件 Fig.5 Load boundary conditions

标准的下颌体部囊性病变三维有限元网格模型，下颌体囊性病变三维有限元模型病变区最大Von Mises应力值，下颌体部囊肿体积及剩余骨厚度测量结果。

建立了下颌体部囊性病变三维有限元网格模型，在模型中根据实验目的施加约束及载荷进行力学分析，建立的模型包括179 374节点和109 618单元。

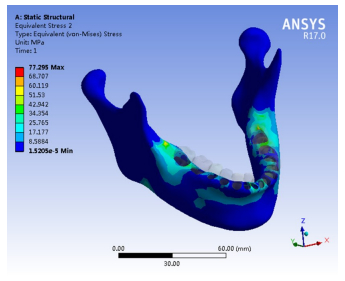
在应力分布云图中默认应力分为9个等级，由蓝色至红色逐渐升高。蓝色表示应力最小，红色表示应力最大，颜色的渐变表示应力的变化。通过云图可以看到最大Von Mises应力值，将此值进行记录，然后与材料的屈服强度相比较，如果在允许的范围内，则可以判断出满足材料的强度要求（图 6）。

图 6(Fig.6)

图 6 Von Mises应力分布云图 Fig.6 Von Mises stress distribution cloud map

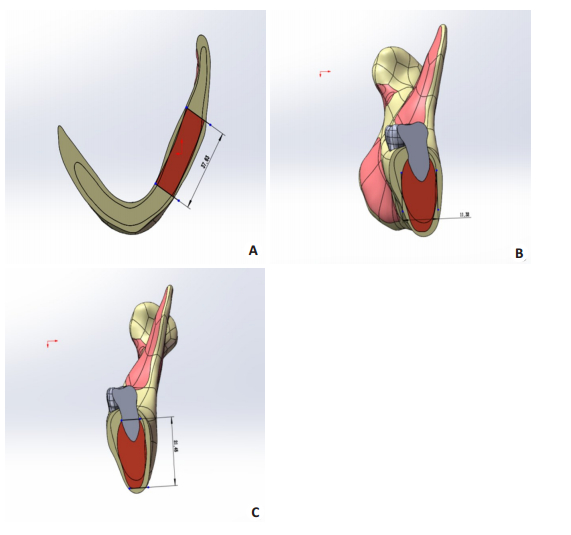
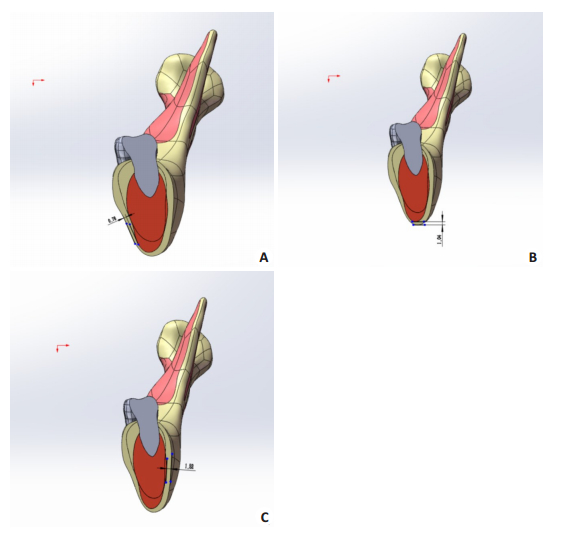
当下颌体部囊肿大小至37.63 mm×11.32 mm× 21.45 mm时，病变区最大Von Mises应力值达到77.295 Mpa，接近下颌骨的屈服强度，存在病理性骨折的风险，此时病变区颊、舌侧及下颌骨下缘剩余骨厚度测量结果分别为1.52、0.76、1.04 mm（图 7、8）。

图 7(Fig.7)

图 7 下颌体部囊肿体积测量图 Fig.7 Measurement of cyst volume in the mandibular body. A: Length of the cyst; B:Width of the cyst; C: Height of the cyst

图 8(Fig.8)

图 8 下颌体部囊性病变区剩余骨壁测量图 Fig.8 Measurement of residual bone wall thickness in cystic lesion area of the mandibular body. A: Lingual bone wall; B: Thickness of the lower margin of the mandible; C: Buccal bone wall

有限元方法分析结果受诸多因素的影响^[22-23]，例如网格划分的质量、几何形状相似性、边界条件设定等，均影响分析结果的精确性，而本研究中通过三维CT扫描图像直接提取下颌骨的几何形态，这就为后续几何模型的准确性提供了保障，在此基础上建立的下颌骨囊性病变三维有限元模型能够最大程度地反映真实生理结构，同时参考国内外研究^[24-25]，将皮质骨与松质骨材料性质设为连续、均质、各向同性。在对骨骼的有限元分析中，多选用Von Mises应力值作为指标，对颌骨而言当Von Mises应力值大于皮质骨屈服强度时则较易发生骨折，若大于松质骨的屈服强度则可能发生骨裂^[26-27]。对青年人的骨骼研究发现，发生骨骼微损伤的阈值约为60 Mpa^[28]，基于以上报道Murakami等^[21]对下颌骨病变切除后术区的应力做了力学分析，得出结论手术切除下颌骨病变后术区发生病理性骨折所需要的应力远超出于60 Mpa这个临界值，在本研究中定义松质骨屈服强度为13 Mpa，密质骨屈服强度为83.2 Mpa^[17]，在此力学标准的基础上对病变区进行生物力学分析。结果提示囊肿大小至37.63 mm×11.32 mm×21.45 mm时，病变区最大Von Mises应力值达到77.295 Mpa，接近下颌骨的屈服强度，存在病理性骨折的风险，此时病变区颊、舌侧及下颌骨下缘剩余骨厚度分别为1.52、0.76、1.04 mm。将本研究病变区剩余骨量测量结果与下颌体部皮质骨解剖学厚度的研究相比^[29]，此时骨质吸收情况为松质骨完全吸收密质骨大部分吸收，因此若影像学资料提示下颌体部囊性病变区剩余骨量与本研究的分析结果相近，应考虑一期开窗减压联合二期刮治术作为首选。

本研究中模拟的是较为理想状态下的下颌体部囊性病变吸收模型，但从囊肿的生长方式考虑，当病变侵犯范围较大时可引起颌骨的颊舌侧膨隆，且多向骨质薄弱的部位生长^[30]，随之颌骨的生物力学特性也会相应改变。因此本研究认为临床中大型颌骨囊肿直接行刮治术，颌骨发生病理性骨折时，病变范围可能仍超出于本研究的测量结果。有文献^[31]提到发挥切割功能的切牙区域承受载荷后应力值无明显大幅度增加趋势，而发挥主要咀嚼功能的磨牙区域承受载荷后应力值显著增加，这与Möhlhenrich等^[28]的研究结果一致，由此得出结论施加载荷的位置显著影响施加部位的应力，这一观察结果强调了进食软性食物在手术后的重要性，因此临床实际工作中尚需将咬合力大小、骨密度等因素综合考虑在内。

综上所述，研究认为囊性病变引起的大范围皮质骨吸收可致颌骨所受应力增加，下颌体部囊性病变区各壁剩余骨皮质厚度低于1 mm时，直接行刮治术会增加病理性骨折发生的风险，建议采取一期开窗减压联合二期刮治术式作为首选治疗方案。本研究不足之处在于仅模拟分析了下颌体部囊性病变模型，后续会对不同病变部位的颌骨囊肿进行进一步研究并详细分析。