2. 南方医科大学南方医院卫生经济管理科, 广东 广州 510515
2. Department of Economic Management, Nanfang Hospital, Southern Medical University, Guangzhou 510515, China
在生存分析研究中, Cox比例风险模型(Cox模型)是最常用、最经典的方法[1]。Cox模型作为一种半参数模型, 不要求估计资料的生存分布类型, 对基线风险函数未作任何假定, 简洁灵活的优良特性使其在医学研究中得到广泛应用。然而, 应用Cox模型的数据须服从比例风险假定这一前提条件, 而在实际应用中数据往往无法满足该条件[2-4]。加速失效(AFT)模型常作为Cox模型的替代模型[5], 该模型研究协变量与对数生存时间的回归关系, 结果更简单明了[6-7]。但参数AFT模型需要指定生存时间分布, 半参数AFT模型的估计方法则一直处于发展研究中, 且以上两种方法易受到数据维度和删失率影响。生存树和随机生存森林(RSF)作为回归树和随机森林(RF)方法的延伸[8-10], 因其非参数方法的灵活性和适用广泛性, 成为比例风险假设不成立时替代Cox回归模型的热门模型[11-14]。RSF的缺点包括随机森林的常规缺点如变量自相关、变量取值较多时引起的偏倚, 有学者认为条件推断森林(CIF)可解决这些问题[15-17]。目前国内对CIF的研究极少, 仅有杨凯等人对CIF和RF之间进行了比较[18], 李金叶等对其在经济方面进行了实例研究[19]。对于RSF和CIF在生存数据中的应用, 国内尚未有研究。本研究将通过蒙特卡洛模拟和实例研究比较四种模型Cox、AFT、RSF、CIF在生存数据中的预测效果。
1 方法 1.1 随机生存森林随机生存森林(RSF)由Ishwaran于2008年提出, 适用于右截尾的生存数据, 是Breiman随机森林的衍生。作为用于处理生存数据的机器学习方法, 其建树规则与经典随机森林类似。RSF利用bootstrap重抽样方法从原始样本中有放回或无放回抽取多个训练样本集, 并对每个样本集建立二元递归生存树; 在每个结点处, 根据分裂准则将研究对象进行分类, 只随机抽取部分变量作为分割点的候选变量; 最后将这些树的预测结果进行综合, 投票或取平均值作为最终结果。RSF的算法如下:
(1) 通过bootstrap重抽样获得多个新的训练样本集。如果用bagging方法对原始数据集D进行有放回地bootstrap重抽样, 则每个观察单位未被抽到的概率为(1-1/N)N, 其中N为D的样本量, 当N无限大时(1-1/N)N收敛于1/e, 约为0.368, 这表明会有接近37%的原始样本不会出现在bootstrap样本中, 这些数据被定义为袋外数据(out-of-bag data, OOB data)。
(2) 利用步骤1得到的bootstrap样本, 对每一个训练样本集都建立一个二元递归生存树。在树的每个节点处, 根据分裂准则将研究对象进行分类, 只随机抽取部分变量作为分割点的候选变量, 在候选变量中选择能够使子节点的生存情况差别最大的变量及对应分割值作为该节点的分裂。树节点的分裂准则包括log-rank准则、log-rank得分(log-rank score)准则、随机log-rank (log-rank random)准则和事件守恒(converse)准则[20-21], 前2者使用较多。
(3) 重复步骤2, 让生存树尽可能的生长, 直到每个根节点样本量达到所设定最小值且至少有1例发生终点事件。
(4) 对每棵树计算其累积风险函数(CHF)和生存函数(SF), 得到整个森林的平均CHF和平均SF作为后续模型性能评价指标的基础, 其中计算SF采用KaplanMeier法。
(5) 利用步骤1、4所得OOB数据和CHF估计OOB误差, 计算自变量的重要性评分(VIM)以了解自变量对结局变量的预测影响。Breiman证明, 利用OOB数据估计泛化误差是无偏且高效的。
RSF传承了RF许多优点:能处理自变量个数远大于样本量的高维数据, 该优点使其倍受基因学、遗传学领域的高度重视; 其次, 作为非参数模型, RSF对资料类型、自变量和因变量之间的关系没有任何限制, 即使是复杂的非线性关系也可以处理; 还可以计算自变量的重要性评分, 通过OOB估计得到较高的预测准确性, 等等。RSF可通过R语言的randomForestSRC包实现[22]。本文模拟与实例分析中RSF树节点分裂准则均采用log-rank准则。
1.2 条件推断森林条件推断森林(CIF)是条件推断树的集合。CIF构建的方法与RSF基本相同, 但CIF中条件推断树的分裂方式与RSF中二元递归生存树不同。二元递归生存树是根据分裂准则得到对应统计量, 选择使统计量达到最值的变量及分割值作为节点的分裂, 即通过一个准则度量同时实现变量选择和分割值选择。而条件推断树将变量选择算法和分割值选择算法区分开, 通过不同的显著性检验方法先选出分裂变量再选出对应分割值。从而解决RSF在变量取值划分多、共线性等情况下估计不精确的缺点。CIF算法如下:
(1) 通过bootstrap重抽样获得多个新的训练样本集。
(2) 利用步骤1得到的bootstrap样本, 对每一个训练样本集都建立一个条件推断树。在树的每个节点处, 对所有待选变量, 检验其与结局变量间的独立性关系, 选择P值最小的变量作为节点分裂变量。对于普通二分类结局通常采用卡方检验, 对于生存数据通常采用基于log-rank得分的秩检验。在因变量与被选中的分裂变量间通过置换检验尝试所有可能的二元分割, 并选取P值最小的分割。
(3) 重复上述步骤, 直到所有分割都不显著或已到达最小节点为止。
(4) 计算OOB误差、自变量VIM等指标用于后续分析。
CIF可通过R语言的party包实现[23]。
1.3 模型评估我们选用brier score评价所有模型的预测精确度[24]。
在常见的分类问题中, brier score被定义为观测值和实际值的差值均方, 具体如下
| $ BS = \frac{1}{N}\sum\limits_{i = 1}^N {\sum\limits_{j = 1}^R {{{\left( {predic{t_{ij}} - observ{e_{ij}}} \right)}^2}} } $ | (1) |
其中N为样本量, R为类别数, predictij是模型预测第i个个体分类为j的概率, observeij是第i个个体是否分类为j的真实状态, 真实分类为j则observeij值为1, 否则为0。
在生存数据中, brier score被定义为观测生存状况和预测生存状况的差值均方, 可通过个体生存时间t、截尾指示变量δ、样本量N计算, 具体如下
| $ BS\left( t \right) = \frac{1}{N}\sum\limits_{i = 1}^N {\left\{ \begin{array}{l} {\left[ {0 - \hat S\left( {t|x} \right)} \right]^2}\frac{{I\left( {{t_i} \le t, {\delta _i} = 1} \right)}}{{\hat G\left( {{t_i}|x} \right)}} + \\ {\left[ {1 - \hat S\left( {t|x} \right)} \right]^2}\frac{{I\left( {{t_i} > t} \right)}}{{\hat G\left( {t|x} \right)}} \end{array} \right\}} $ | (2) |
其中Ĝ(t|x)是条件生存函数的Kaplan-Meier估计值。对BS积分, 可得到integrated Brier score (IBS)
| $ IBS = \int_0^{\max \left( t \right)} {BS\left( t \right){\rm{d}}t} $ | (3) |
IBS越低, 模型的预测精度越高。IBS的估计可使用R语言的pec包实现[25]。
2 模拟 2.1 模拟设置右删失数据常通过指数分布或均匀分布产生, 本研究选择生成服从指数分布的右删失数据。
设生存时间变量为T, 删失时间变量为L, T和L是独立的连续随机变量。用Ti表示个体i的生存时间, 令(Ti, Li)相互独立。截尾指示变量δi=Ι[Ti ≤ Li], 其中Ι[∙]为示性函数。若Ti ≤ Li, 则δi=1, 表示发生终点时间, 否则δi=0, 表示删失。最后将所有删失个体的观测时间记录为ti=Li, 非删失个体的观测时间记录为ti=Ti。
为了比较Cox模型、AFT模型、RSF模型和CIF模型对样本人群生存情况的预测精度, 我们设置了若干个不同情况下的模拟试验进行考察, 通过改变删失时间Li的指数分布参数来模拟不同删失率, 通过改变生存时间Ti的指数分布参数来模拟数据自变量信息不同的情况(表 1)。
| 表 1 模拟数据集的参数设置 Tab.1 Parameter setting for each simulated dataset |
数据集A、B、C、D研究自变量中的分类变量分别为二分类和多分类时4种模型对观察对象生存情况的预测能力, 这4个数据集都包含10个自变量, 5个自变量x1i-x5i为定量变量, 另外5个自变量x6i-x10i为分类变量, 其中只有2个变量(定量变量x1i和分类变量x6i)与结局有关。数据集A、C中的分类变量为二分类, B、D中的分类变量为多分类。
对于数据集A、B, 设定其自变量相互独立, 故A、B研究自变量独立时自变量中的分类变量分别为二分类和多分类时4种模型对样本生存情况的预测能力。数据集C、D中, 均设定x1i与x6i有交互作用, 交互项系数均设为2, 故C、D研究自变量存在交互时, 交互项中的分类变量分别为二分类和多分类时4种模型对样本生存情况的预测能力。
数据集E包含5个自变量, 设定为多元正态分布, 两两间相关系数设为0.2, 5个自变量都与结局有关, 故该数据研究自变量相关时4种模型对样本生存情况的预测能力。
数据集F、G研究自变量个数变化时4种模型对样本生存情况的预测能力, 设定这2个数据集的自变量都独立且服从相同的正态分布, 其中F包含5个自变量, G包含50个自变量, 但均只有5个自变量与结局有关。
蒙特卡洛模拟次数设置为1000次, 样本量设置为200、400、600、800、1000, 删失率设置为0、0.1、0.2、0.3、0.4、0.5。为了使得4种方法的预测精度具有可比性并避免自身拟合造成的过拟合现象, 对每次模拟产生的数据集, 我们随机选取其中的80%作为训练集拟合4个模型, 剩余的20%作为测试集得到4种模型的预测精度指标IBS, 最后用所有模拟结果的IBS平均值作为评估指标。
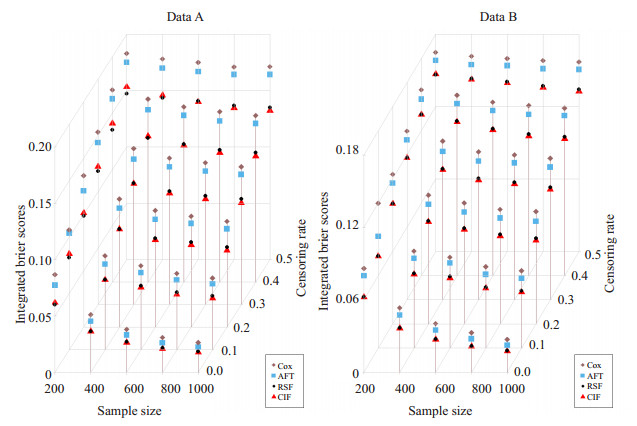
2.2 模拟结果自变量独立时, 其中的分类变量分别为二分类(数据集A)和多分类(数据集B)时4种方法的预测能力模拟结果见图 1。可见, 4种模型的IBS均随样本量增大而减小, 随删失率增大而增大, 两种森林模型RSF、CIF预测效果均优于Cox、AFT模型。CIF模型在A中与RSF的预测效果各有优势, 在样本量为200时IBS始终大于RSF, 随样本量增大IBS开始接近并逐渐小于RSF。而在B中预测效果优于RSF, 且随样本量和删失率增大优势增大。
|
图 1 数据集A和B在不同样本量和删失率下的IBS变化情况 Fig.1 Integrated Brier scores of data A and B under different sample sizes and censoring rates. |
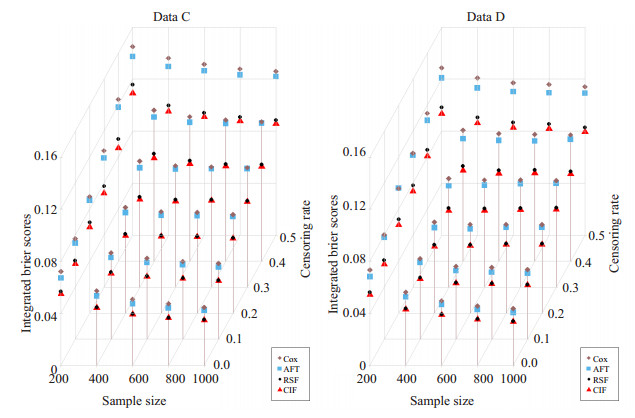
自变量存在交互时, 其中的分类变量分别为二分类(数据集C)和多分类(数据集D)时4种方法的预测能力模拟结果见图 2。此时4种模型的IBS都随删失率增大而增大, 大部分都随样本量增大而减小, 一些随样本量增大而趋于稳定。两种森林模型RSF、CIF预测效果均优于Cox、AFT模型, 其中CIF模型的预测效果均优于RSF, 而这种优势随删失率增大而增大。
|
图 2 数据集C和D在不同样本量和删失率下的IBS变化情况 Fig.2 Integrated Brier scores of data C and D under different sample sizes and censoring rates. |
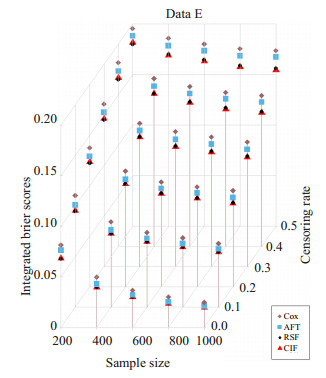
自变量相关时4种方法对样本生存情况的预测能力见图 3。可见4种模型的IBS均随样本量增大而减小, 随删失率增大而增大。两种森林模型RSF、CIF预测均优于Cox、AFT模型, CIF模型在样本量为200时的IBS与RSF相近甚至更大, 但在其他情况下优于RSF, 且优势随样本量和删失率增大而增大。
|
图 3 数据集E在不同样本量和删失率下的IBS变化情况 Fig.3 Integrated Brier scores of data E under different sample sizes and censoring rates. |
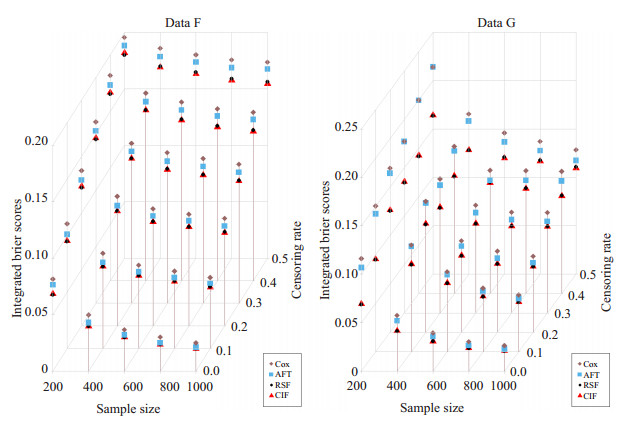
自变量个数变化时, 其中的变量个数分别为5个(数据集F)和50个(数据集G)时4种方法的预测能力模拟结果见图 4。可见4种模型的IBS均随样本量增大而减小, 随删失率增大而增大。两种森林模型RSF、CIF预测均优于Cox、AFT模型, 且对自变量个数变化敏感度均低于Cox、AFT模型, G在样本量为200时, 两类森林模型的IBS远低于Cox、AFT模型, 而这种优势随样本量增大而减弱。CIF模型在样本量为200-400时的IBS与RSF相近甚至更大, 但在其他情况下略优于RSF, 且优势随样本量和删失率增大而增大。
|
图 4 数据集F和G在不同样本量和删失率下的IBS变化情况 Fig.4 Integrated Brier scores of data F and G under different sample sizes and censoring rates. |
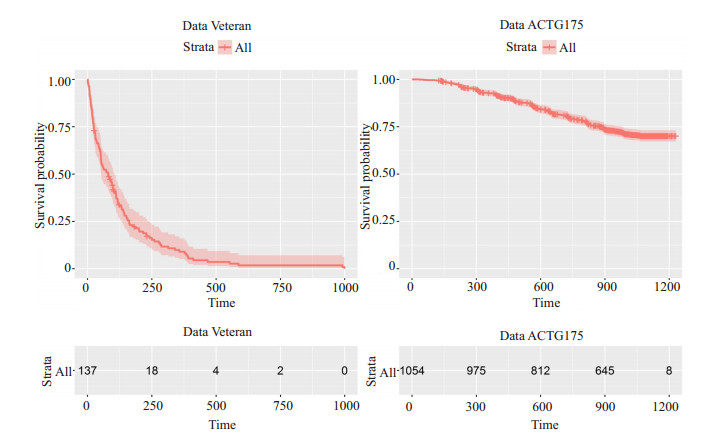
实例1选自R语言survival包的Veteran数据集[26], 源于退伍军人管理局的一项肺癌随机化研究。Veteran中包含137例数据, 8个变量, 其中中位生存时间为80 (range:1~999), 有128例发生终点事件, 数据删失率为6.6%。表 2列出该数据集除生存时间time和截尾指示变量status外剩余6个基线指标的基本信息, 图 5中左图为该数据的生存曲线图。
|
图 5 实例Veteran数据集和ACTG175的生存曲线图 Fig.5 Survival curves generated from Veteran and ACTG175 datasets. |
| 表 2 Veteran数据集的基线指标分布 Tab.2 Characteristics of the covariates in Dataset Veteran [Mean± SD or n (%)] |
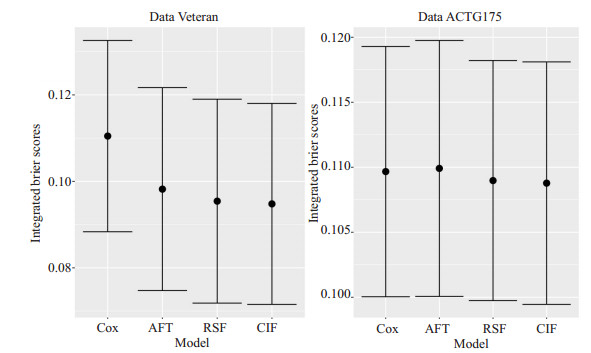
对Veteran数据集, 我们选取time和status作为生存时间和截尾指示变量, 其余6个变量作为自变量, 随机选取数据集的80%样本作为训练集拟合4种模型, 剩余的20%作为测试集得到4种模型的预测精度指标IBS, 对该过程重复100次得到IBS平均值作为评价指标。图 6中左图显示了4种模型拟合的IBS误差限图, 从均值来看此时AFT、RSF、CIF模型的IBS均值相近, 其中CIF的均值最小且标准差最小, 说明在有多分类变量时CIF的预测精度较高且较为稳定。
|
图 6 实例Veteran数据集和ACTG175的IBS误差限图 Fig.6 Integrated Brier scores of Veteran and ACTG175 datasets. |
实例2选自R语言speff2trial包的ACTG175数据集[27], 来自艾滋病临床试验组175研究。此项研究包含CD4 T细胞计数在每立方毫米200至500之间的2139个艾滋病患者, 每位患者有27个变量。本文选取联合用药组(zidovudine和didanosine) 522例和单独用药组(zidovudine) 532例的病人共1054例作为研究对象, 其中284例发生终点事件, 数据删失率为73.1%。本文选取除生存时间days和截尾指示变量cens外其余含义不重复的16个变量作为自变量。表 3列出选取16个基线指标的基本信息, 图 5中右图为该数据的生存曲线图。
| 表 3 ACTG数据集的基线指标分布 Tab.3 Characteristics of the covariates in Dataset ACTG175 |
图 6中右图显示了ACTG175数据集中四种模型拟合的IBS误差限图, 从均值来看此时四种模型的IBS均值相近, 但其中CIF的均值最小且标准差最小, 说明在该大样本、高删失、有多分类变量的数据集中, CIF的预测精度较高且较为稳定。
4 讨论本文比较了Cox、AFT、RSF、CIF 4种模型的预测能力, 采用IBS作为评估指标。通过模拟产生7种情形下的数据, 包含自变量独立、自变量含多分类变量、自变量交互、自变量相关、自变量个数变化的情况。结果显示, 4种模型的预测能力都随样本量增大、删失率减小而增大。两种生存森林模型RSF、CIF在模拟中预测能力均优于Cox、AFT模型, 且在自变量个数发生变化时可以看出RSF、CIF预测更优且更稳定。对两种生存森林模型RSF、CIF的IBS进行比较, 可以看到样本量较小(文中为200、400)时, 在多数情况下如自变量独立(数据A、B)、自变量相关(数据E)、自变量个数变化(数据F、G)时RSF略低于CIF, 而在样本量大、删失率大、自变量包含多分类变量的情况下CIF的IBS多低于RSF且这种优势随样本量增大、删失率增大而增大。两个实例研究分析结果显示CIF的IBS均值最低且更加稳定, 该研究印证了CIF在有多分类变量的情况下预测能力可能优于RSF。
本研究说明了CIF的预测能力在数据存在多分类变量、共线性、存在交互项、删失率大等情况可能优于RSF, 但可以看到在一些情况下如样本量小、不存在多分类变量、数据完全是独立连续变量时CIF预测与RSF相比不具有优势或更弱。实例1分析结果显示AFT模型的预测能力与两种森林模型相差不大, 这说明在数据不复杂的情况下, 传统参数或半参数模型的预测能力不一定明显低于森林模型, 并且能给出较为简单易懂的回归结果。
综上所述, 在对生存数据进行分析时, 研究者应根据数据本身信息做出选择合适的分析方法。若数据构造不复杂且满足传统模型如Cox、AFT的前提, 我们推荐采用传统的回归模型。若数据构造复杂如高维、非线性等情况, 我们推荐采用生存森林模型, 其中对于自变量包含多分类变量、可能存在相关或交互项的生存数据, 尤其该数据样本量大、删失率高时我们推荐采用CIF进行预测; 对于样本量小、删失率小、不包含多分类变量、数据完全独立的生存数据我们推荐采用RSF进行预测。
近年来, 森林模型在理论和方法上都引起较大关注并得到很多学者的研究与拓展。然而CIF模型尽管在较多情况下具有优势, 国内对其研究和应用却始终较少, 而更没有引进生存分析领域。我们期望借本研究将CIF引入国内医学研究领域, 引起更多国内学者关注, 未来也会对CIF进行进一步研究。
| [1] |
Cox DR. Regression models and life tables[J]. J Roy Stat Soc Ser B, 1972, 34(2): 187-220. |
| [2] |
Platt RW, Joseph KS, Ananth CV, et al. A proportional hazards model with time-dependent covariates and time-varying effects for analysis of fetal and infant death[J]. Am J Epidemiol, 2004, 160(3): 199-206. |
| [3] |
Ng' andu NH. An empirical comparison of statistical tests for assessing the proportional hazards assumption of cox's model[J]. Stat Med, 1997, 16(6): 611-26. |
| [4] |
Fisher LD, Lin DY. Time-dependent covariates in the cox proportional-hazards regression model[J]. Annu Rev Public Health, 1999, 20(1): 145-57. |
| [5] |
Khan MHR, Bhadra A, Howlader T. Stability selection for lasso, ridge and elastic net implemented with AFT models[J]. Stat Appl Genet Mol Biol, 2019, 18(5): 125-6. |
| [6] |
黄福强.含治愈个体生存资料的分析策略和亚组识别研究[D].南方医科大学, 2019.
|
| [7] |
康佩, 许军, 黄福强, 等. Adaptive Elastic Net结合加速失效时间模型在亚组识别中的应用[J]. 南方医科大学学报, 2019, 39(10): 1200-6. |
| [8] |
Breiman L, Friedman J, Stone CJ, et al. Classification and regression trees[M]. Belmont: CRC press, 1984.
|
| [9] |
Breiman L. Random Forests[J]. Mach Learn, 2001, 45(1): 5-32. |
| [10] |
Ishwaran H, Kogalur UB, Blackstone EH, et al. Random Survival Forests[J]. Ann Appl Stat, 2008, 2(3): 1214. |
| [11] |
Ishwaran H, Udaya B, Kogalur. Consistency of random survival forests[J]. Stat Probabil Lett, 2010, 80(13/14): 1056-64. |
| [12] |
Bou-Hamad I, Larocque D, Ben-Ameur H, et al. A review of survival trees[J]. Stat Surv, 2011, 5: 44-71. |
| [13] |
Fernández T, Rivera N, Teh YW. Gaussian processes for survival analysis[C]. New York: Curran Associates, 2016, 5015-23.
|
| [14] |
高珍, 柯阿香, 余荣杰, 等. 基于随机生存森林的交通事件持续时间预测[J]. 同济大学学报:自然科学版, 2017, 45(9): 1304-10. |
| [15] |
Das A, Abdel-Aty M, Pande A. Using conditional inference forests to identify the factors affecting crash severity on arterial corridors[J]. J Saf Res, 2009, 40(4): 317-27. |
| [16] |
Wright MN, Dankowski T, Ziegler A. Unbiased split variable selection for random survival forests using maximally selected rank statistics[J]. Stat Med, 2017, 36(8): 1272-84. |
| [17] |
Nasejje JB, Mwambi H, Dheda K, et al. A comparison of the conditional inference survival forest model to random survival forests based on a simulation study as well as on two applications with time-to-event data[J]. BMC Med Res Methodol, 2017, 17(1): 115. |
| [18] |
杨凯, 侯艳, 李康. 条件推断森林在高维组学数据分析中的应用[J]. 中国卫生统计, 2016, 33(2): 215-8. |
| [19] |
李金叶, 郝雄磊. 机会不平等的测度:回归树模型的应用与比较[J]. 统计与信息论坛, 2019, 34(10): 3-13. |
| [20] |
Lausen B, Schumacher M. Maximally selected rank statistics[J]. Biometrics, 1992, 48(1): 73-85. |
| [21] |
Hothorn T, Lausen B. On the exact distribution of maximally selected rank statistics[J]. Comput Stat Data Anal, 2003, 43(2): 121-37. |
| [22] |
Ishwaran H, Kogalur UB. randomForestSRC: random forests for survival, regression and classification (RF-SRC). R package version 1.4.0.2014.https: //cran.r-project.org/.
|
| [23] |
Hothorn T, Hornik K, Strobl C, Zeileis A. Party: a laboratory for recursive partitioning. R package version 1.0-23.2015. https: //cran.r-project.org/
|
| [24] |
Ishikawa Sohta A, Zhukova Anna, Iwasaki Wataru, et al. A fast likelihood method to reconstruct and visualize ancestral scenarios[J]. Mol Biol Evol, 2019, 36(9): 2069-85. |
| [25] |
Mogensen UB, Ishwaran H, Gerds TA. Evaluating random forests for survival analysis using prediction error curves[J]. J Stat Softw, 2012, 50(11): 1-23. |
| [26] |
Kalbfleisch JD, Prentice RL. The statistical analysis of failure time data[J]. IEEE T Reliab, 1986, 34(1): 11. |
| [27] |
Hammer SM, Katzenstein DA, Hughes MD, et al. A trial comparing nucleoside monotherapy with combination therapy in HIV-infected adults with CD4 cell counts from 200 to 500 per cubic millimeter.. AIDS Clinical Trials Group Study 175 Study Team[J]. New Engl J Med, 1996, 335(15): 1081-90. |
 2020, Vol. 40
2020, Vol. 40

