2. 西安交通大学计算机科学与技术学院,陕西 西安 710049
2. School of Computer Science and Technology, Xi'an Jiaotong University, Xi'an 710049, China
肿瘤异质性促使肿瘤在演化过程中呈现高度复杂性和遗传多样性,肿瘤组织内共存多个细胞亚群造成细胞差异、表型差异及治疗敏感性差异[1],是导致治疗失败的关键因素[2]。目前,肿瘤异质性侧重于基因型层面的研究,而单体型层面的研究相对匮乏[3]。Knudson在癌变理论中证明了肿瘤单体型的重要性[4],单体型不仅可以发现各变异间复杂的异质性关系和驱动变异,而且在基因疾病诊断、关联研究、祖先推理和药物设计等领域发挥着重要作用。单体型可由生物学实验方法直接获取[5],但时间与成本代价太高,因此通常采用计算方法识别单体型,主要分为种群单体型和个体单体型两类重建计算问题。其中,种群单体型重建依赖于家族谱系结构或单体型块间连锁不平衡性,如Browning等[6]基于近距离标记倾向于连锁不平衡的事实,采用统计推断技术识别种群单体型。Lancia首次引入直接根据测序片段实现个体单体型组装问题[7],此类算法主要采用启发式策略,其中最少错误修正函数被广泛使用[8]。Wang等[9]在聚类算法中引入距离函数实现比对读段与单体型的对应关系;HASH[10]为一种马尔科夫链蒙特卡洛算法,但此方法计算成本相对较高。MixSIH方法[11]运用概率模型确定SNP位点间的连接方式,该方法时间复杂度随SNP位点的数量呈指数级增长。此外,遗传算法[12]和粒子群算法[13]也被相继应用于单体型组装问题中。
尽管在种群和个体单体型识别方面开展了大量研究,但并不适用于肿瘤克隆单体型识别问题。其一,种群单体型定相方法依赖于家族谱系结构和连锁不平衡性,而肿瘤亚克隆变异位点的产生具有极高随机性,相互之间的连接不能依赖连锁不平衡性来实现,所以基于群体基因型数据的单体型定相方法无法解决肿瘤单体型重建问题。其二,肿瘤基因组中包含相互关联的多层级亚克隆形成多倍体基因型,适用于二倍体基因组的单体型组装算法无法有效地解决肿瘤组织中多级亚克隆单体型识别问题。此外,大多数单体型组装问题都是NP难问题,若肿瘤序列具有m个杂合型单核苷酸变异位点,将产生2m条候选单体型,如何从大量候选单体型中有效区分每条克隆单体型具有很大的挑战性。
本文利用具有长读段优势的三代测序数据,提出一种基于最大生成树的肿瘤克隆单体型重构算法。通过提取变异位点信息推断其连接关系的最大生成树,并遵循肿瘤克隆间继承原则逐级扩展最大生成树,从而实现肿瘤克隆单体型重构。假设肿瘤样本中的克隆数目为C,变异位点总数为N,亚克隆的基因型数据集合G= {G0, …,Gi, …,GC-1},Gi为第i种克隆的基因型。αi表示第i种克隆基因型的占比,满足关系式:α0+α1+ … +αC-1=1。算法目标是根据测序的读段数据集合重构亚克隆单体型H={h0,h1, …,h2C-1},其中(h2i,h2i+1)为第i种亚克隆单体型对,其对应的基因型为Gi。该方法在各种贴近真实数据特征的实验中取得了良好效果。
1 基于最大生成树的单体型重构算法 1.1 算法思想将肿瘤样本中识别的变异位点看作为图的顶点,将变异位点对之间的连接关系看作图的边,基于概率函数计算边的权值,从而将克隆单体型重构问题转换为无向图中搜索最大生成树问题。具体算法过程分为以下4步:
第1步,采用SciClone方法[14]聚类位点变异频率,解出亚克隆个数的一个先验,作为构建单体型的先验信息。令M为所有变异位点的集合,M=∪Mi(i∈[0..C-1]),Mi为亚克隆Si中包含的变异位点集合,即Mi={p1, ⋯,pu, ⋯,pv, ⋯,pni},ni为亚克隆Si的变异位点数目,(pu,pv)表示有连接关系的变异位点对,HSipu,pv表示变异位点pu与pv在亚克隆Si单体型中的连接模式。第2步,构建基础克隆变异位点的最大生成树。首先根据基础克隆S0的变异位点集合M0及其变异位点对之间的连接关系,构建一个基础克隆无向图U0=(V0,E0),其中V0=M0表示变异位点构成的顶点集合;E0表示V0顶点对之间的连接关系,若(pu,pv) ∈E0,则表示顶点pu∈V0,pv∈V0间存在连接关系且其对应的边权值函数为w(pu,pv),即pv与pu的连接概率。由此,基础克隆变异位点之间的连接模式问题转变为在无向图U0=(V0,E0)中搜索最大生成树T0=(VT0,ET0)问题,其中,VT0=V0,ET0⊆E0。第3步,剥离厚度后扩展最大生成树。按照肿瘤克隆在其线性演变模式中的分化级别,在上级生成树Ti-1=(VTi-1,ETi-1)的基础上逐层扩展下级克隆Si中的变异位点集合Mi及其与图中变异位点之间的连接关系,形成无向图Ui=(Vi,Ei),其中Vi=Vi-1∪Mi,Ei=ETi-1∪ {Mi之间及Mi与Vi-1之间的连接关系}。对无向图Ui求解在Ti-1基础上的扩展最大生成树Ti=(VTi,ETi),从而确定Si中所有变异位点Mi的连接模式。第4步,重构克隆单体型。如此迭代扩展所有亚克隆,逐步获得各级亚克隆变异位点之间的连接模式,实现肿瘤克隆单体型重构。
1.2 构建基础克隆变异位点的最大生成树从克隆间继承原则可知,基础克隆S0在肿瘤总体的进化过程中,一旦其连接方式确定,在后继的亚克隆Si(i∈[1..C-1])分化中仍会继承这种连接方式。根据此特性,基于最大生成树算法的克隆单体型重构方法遵循克隆间变异继承原则,以基础克隆S0的变异位点集合M0为起始,按照肿瘤克隆在其线性演变模式中的分化级别逐层分离克隆中的变异位点,自顶至底依次扩展最大生成树。在最大生成树的构建中,构建出的上一级亚克隆单体型结构作为已知条件,指导下一级亚克隆单体型的重构。
假设基础克隆S0中存在一个变异位点对(pu,pv),则HS0pu,pv可能的取值为两种组合方式,即{(0, 0), (1, 1)}和{(0, 1), (1, 0)},0与1分别表示与参考基因组匹配和不匹配的碱基。在计算变异点对(pu,pv)的覆盖度时,仅统计同时跨越变异点对(pu,pv)的读段数目。F(u,v)表示同时跨越变异点对(pu,pv)的读段集合,NF(u,v)表示集合F(u,v)中的读段个数。根据各种连接模式的概率值建立相应的无向加权图U0。令{(0, 0), (1, 1)}型连接模式的概率为正,即p(HS00, 0 ∧p(HS01, 1) > 0;{(0, 1), (1, 0)}型连接模式的概率为负,即p(p(HS00, 1∧p(HS01, 0)<0。根据基础克隆位点的总体覆盖度设定支持度阈值δc,即支持变异点对(pu,pv)正确连接的可信度阈值。若NF(u,v)≥δc,视此变异点对之间存在一条边,边上的权值为连接的概率值。权值的计算过程如下:
(1) 首先统计变异点对在不同联合等位基因状态下的读段数量。
| $ {N^{{b_{{p_u}, }}{b_{{p_v}}}}}\left( {{p_u}, {p_n}} \right) =\sum\limits_{r \in F(u, n)} I \left( {r\left( {{p_u}, {p_v}} \right) =\left( {{b_{{p_i}}}, {b_{{p_i}}}} \right)} \right) $ | (1) |
式中:
(2) 计算变异点对之间的连接概率。对于变异位点pu,与其具有连接关系的变异点对pv的碱基状态可能为0或1两种情况。将每个点的测序误差和比对误差ε考虑其中,则与pu连接的变异位点pv可能的两种连接概率为f(bpu,x),x∈(0, 1)。
| $ \begin{array}{l} f\left( {{b_{{p_u}}}, x} \right) =\\ \frac{{\left( {{{(1 -\varepsilon )}^2} + {\varepsilon ^2}} \right) \times {N^x}\left( {{p_u}, {p_x}} \right)}}{{{N_{F(u, v)}}}} + \frac{{2\varepsilon (1 -\varepsilon ) \times {N^{1 -x}}\left( {{p_u}, {p_v}} \right)}}{{{N_{F(u, v)}}}} \end{array} $ | (2) |
(3) 计算权值
| $ {w\left( {{p_u}, {p_v}} \right) =f\left( {{b_{{p_u}}}, 0} \right) -f\left( {{b_{{p_u}}}, 1} \right)} $ | (3) |
根据权值的正负判定变异点对(pu,pv)的连接模式:若w(pu,pv) > 0,则(pu,pv)的连接模式为HS00, 0或HS01, 0;若w(pu,pv)<0,则(pu,pv)的连接模式为HS00, 1或HS01, 1。w(pu,pv)的绝对值越大,表示对应连接模式的可信度越高。
将基础克隆中所有变异位点按照上述权值计算过程(1)~(3)构建一个无向加权图U0(V0,E0),其中,V0 =M0,令V0中顶点数目为Nv。设标志数组为f[Nv],f[v] =1/0表示第v个顶点已加入/未加入生成树;将基础克隆中所有顶点的初始标志位设为0,即f[v] =0,v∈[1,Nv]。构造图U0对应的初始最大生成树T0(VT0,ET0)。最大生成树算法的构建流程如算法1示意。
| Algorithm 1: Building algorithm of the maximum spanning tree Ti(i∈[0,C-1]). | |
| Input: undirected weighted graph Ui(Vi,Ei), upper level maximum spanning tree Ti-1(VTi-1,ETi-1), the number of mutations in Mi is ni. Output:maximum spanning tree Ti(VTi,ETi) and the haplotypes of sub-clone Si. | |
| 1. | if(i=0){ //Initialization,set the number of mutations in Vi is Nv |
| 2. | Initializing flag array f[Nv]: for(v=1;v≤Nv;v++)f[v]=0; |
| 3. | Randomly selecting a vertex sp in the graph Ui as starting point of reconstructing clonal haplotypes; |
| 4. | ni--; |
| 5. | Initializing the maximum spanning tree Ti: the vertex set is VTi={sp}, the edge set is ETi={ET0} andf[sp] =1; |
| 6. | } else { |
| 7. | Initializing flag array f[Nv]: for(v=1;v≤Nv;v++){if(v∈VTi-1)f[v]=1; elsef[v]=0; } |
| 8. | Initializing maximum spanning tree Ti:VTi=VTi-1,ETi=ETi-1; |
| 9. | } |
| 10. | for(j=1;j≤ni;j++) { |
| 11. | Finding all the edges about (pu,pv) that (pu∈VTi∧pv∈Vi-VTi) from graph Ui; |
| 12. | Selecting edge (pu,pv) with max(|w(pu,px)|) to add into the edge set ETi of Ti,pv is added into vertex VTi; |
| 13. | Determine the base state of pv according to the sign of w(pu,pv); |
| 14. | Updating f[pv] with 1; |
| 15. | } |
| 16 | End of algorithm, attaining the maximum spanning treeTi. |
根据基础克隆中变异位点间连接关系构建初始最大生成树T0后,仅仅确定了单体型中属于基础克隆的变异位点的连接模式,其余的变异位点分布于其它亚克隆中,需进一步采用厚度剥离方法按照克隆间继承原则逐级扩展最大生成树。假设对亚克隆Si包含的变异位点扩展最大生成树,则需要实现前i-1个亚克隆的厚度剥离。厚度剥离指在等位基因方向上将所有的克隆分成两部分:被剥离的亚克隆集合{Sk:k∈[0..i-1]}和余下的克隆集合{Sk':k' ∈[i..C-1]}。根据亚克隆Sk的混合占比将其从混合的测序数据中分离出去,实现等位基因为0的厚度剥离,等位基因为1的厚度保持不变。根据剥离厚度调整变异位点对(pu,pv)对应的覆盖度,计算公式为:
| $ {\widetilde {{N^0}}\left( {{p_u}, {p_v}} \right) ={N^0}\left( {{p_u}, {p_v}} \right) -{N_{F(u, v)}} \times \left( {\sum\limits_{0 \le k < s({p_v})} {{\alpha _k}} } \right)} $ | (4) |
式中:s(pv)——变异位点pv所属的亚克隆;αk——亚克隆Sk的混合占比。
将数据分离后,采用与无向加权图U0相同的构建方法,建立新的无向加权图Ui,利用公式(4)更新公式(2)中的N0(pu,pv)。当|w'(pu,pv)| >δw时,表示(pu,pv)变异点对之间存在有效边,则将其加入到图Ui中,对应的权值为w'(pu,pv)。δw默认值为0.1。图Ui构建完毕,基本可以包含亚克隆Si中所有的变异位点。然后根据图Ui扩展最大生成树为Ti。由于在建图Ui时采用了厚度剥离方法,若剥离厚度不精确,可造成图Ui中的边权值偏差。为了减小边权值偏差的影响,在已知变异位点pu的情况下确定扩展树Ti中变异位点pv的碱基状态时,需联合图Ui中所有和pv有边连接且状态已知的顶点进行综合评分来确定。将图Ui中所有顶点处理完成后,扩展树Ti也构建完成。
亚克隆数目为C,亚克隆Si包含的变异位点集合为Mi,采用克隆迭代方法逐级实现变异位点集合的最大生成树扩展过程如算法2所示:
| Algorithm 2: Extending algorithm of the maximum spanning tree T. | |
| Input: the set of mutations Mi contained by sub-clone Si; the ratio of Si is αi,i∈[0,C-1]; the information of alignments(reads related mutations). Output: the maximum spanning treeT. | |
| 1. | Initating U-1(φ, φ) and T-1(φ, φ); |
| 2. | for(i=0;i<C;i+ +){ |
| 3. | Vi=Vi-1∪Mi;//extending the set of Viin the undirected graph Ui(Vi,Ei); |
| 4. | Ei=ETi-1∪{the relation of edge between Mi s and between Mi and Vi-1} |
| 5. | Peering the depth of S0-Si-1 from Mi; |
| 6. | Re-computing the weight of new added edges between mutations. |
| 7. | Calling algorithm1 to extend the maximum spanning tree Ti. parameters: undirected weight graph Ui(Vi,Ei); upper maximum spanning tree Ti-1(Vi-1,ETi-1), the number of mutations in Miis ni; |
| 8. | Saving the connection mode between mutations of sub-clone Si, that is, haplotypes; |
| 9. | } |
| 10. | End of algorithm,TC-1(VC-1,ETC-1) is the final extended maximum spanning treeT. |
为了最终识别出包含所有变异位点的完整单体型,需要保证最终扩展的最大生成树T中包含所有的变异位点。当测序覆盖度较低时,若支持度阈值设得较高,会使某些变异位点没有被扩展树T所包含。由此需要根据覆盖度调整支持度阈值δc和权值阈值δw,尽可能的保证低漏点率。
1.4 重构克隆单体型采用深度优先遍历扩展树T中所有顶点,并将这些顶点按照参考序列中的相对位置进行先后排序,排序后各顶点的状态集合即为最后一个亚克隆的一条单体型。在假设所有变异位点都是杂合型的前提下,依据各亚克隆之间线性进化关系,采用以下公式求得其余亚克隆的父链单体型。
| $ {h_{2i,j}} = \left\{ {\begin{array}{*{20}{l}} {0;{h_{2(i + 1),j}} = 0}\\ {1;{h_{2(i + 1),j}} = 1\;{\rm{and}}\;sub(j) \le i}\\ {0;{h_{2(i + 1)j}} = 1\;{\rm{and}}\;sub(j) > i} \end{array}} \right. $ | (5) |
式中:i——亚克隆号;j——变异位点标号;sub(j)——变异位点j所属的亚克隆号;h2i,j——第i个亚克隆第j位点上的父链碱基状态。
最后,根据得到的父链克隆单体型求解对应母链单体型上的位点碱基状态,
| $ {{h_{2i + 1, j}} =\left\{ \begin{array}{l} {h_{2i, j}} \oplus 1;{\mathop{sub}\nolimits} (j) \le i\\ {h_{2i, j}};i < {\mathop{sub}\nolimits} (j) < C -1 \end{array} \right.\;\;\;\;\;\;0 \le i < C -1\;} $ | (6) |
为检测文中所提方法的实用性,将本文所提的算法实现称为CloneHap软件。三代测序数据采用仿真软件PBSim[15]和TNSim[16]生成,使用软件BLASR[17]实现三代测序数据中的读段与参考序列的比对。由于测序覆盖度、体细胞变异率、亚克隆数目和混合比例以及读段长度等参数变化对方法均产生影响,所以每次只改变其中一个参数值对实验结果进行比较分析,其余参数均取默认值。各参数的默认值设置如下:(1)亚克隆数目,Kandoth等[18]对12种主要癌症类型的变异模式进行了分析,研究表明肿瘤内3~4个亚克隆较常见。所以,本文设置克隆数目的默认值为3;(2)覆盖度,Wendl[19]利用数学模型证明得出,肿瘤/正常样本研究中肿瘤样本比正常样本的测序深度应更高,且提出若要较好地满足实验需求,肿瘤样本和正常样本的覆盖度需分别达到26倍和21倍以上。由此,同时考虑多个亚克隆存在的情况,保证每个克隆中变异位点有足够的读段覆盖度。本文设定覆盖度默认值为30×;(3)读段长度,文献[20]表明三代测序的读段长度可达到5~120 kbp,仿真工具PBSim对三代测序的读段长度也进行了分析,实验表明读段长度可达到5860~22 842 bp。所以,在本实验中设置读段长度的默认值为15 kbp;(4)遗传变异率参照JointSNVMix[21]中的设置,默认值设为0.1%;对于体细胞变异率,主要考虑一条长读段同时覆盖至少两个以上的变异位点才能有效确定单体型,当读段长度为15 kbp时,变异率应至少为0.01%,所以默认值设置为0.01%;(5)混合比例,其设置应该保证各亚克隆的变异频率具有一定的区分性,由此保证聚类效果,比例差异越大聚类效果越好,因此设置默认值为3:5:2。
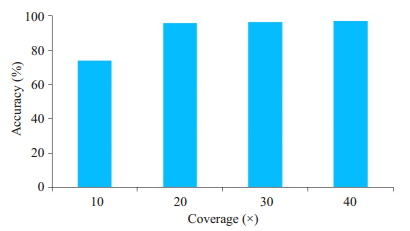
(1) 不同覆盖度下的性能分析。覆盖度分别设置为10×、20×、30×和40×,单体型识别准确率如图 1所示。从图可见,覆盖度低于20×时,准确率偏低,且准确率随着覆盖度的增加而增加。当测序覆盖度为10×时,由于3个亚克隆的比例为3:5:2,所以亚克隆S2的平均覆盖度为2×,则其每条单体型的测序覆盖度为1×左右,导致一些变异位点无法被采样到,增加了构图时的漏点率,从而导致最终识别的单体型准确率偏低。由此,CloneHap方法提出最低覆盖度为20×的需求。
|
图 1 不同覆盖度下的识别准确率分析 Fig.1 Analysis of recognition accuracy under different coverage. |
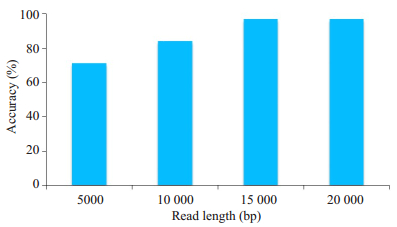
(2) 不同读段长度下的性能分析。选择四种读段长度进行性能分析,从图 2可见,当读段长度较短时,单体型的准确率较低,只有70%左右,准确率随着读段长度增长而得到明显提升。当读段长度达到15 000 bp时,单体型准确率趋于稳定。充分表明,当一条读段跨越一定数目的变异位点时,单体型识别准确率即可得到保证。
|
图 2 不同读段长度下识别准确率分析 Fig.2 Analysis of recognition accuracy under different read lengths. |
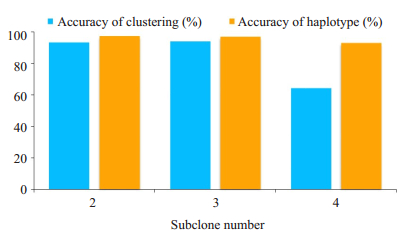
(3) 不同亚克隆数目下的性能分析。肿瘤异质性越复杂其包含的亚克隆数目越多,本组实验主要针对不同亚克隆数目的算法性能进行测试,如图 3所示。由于CloneHap方法依赖于对变异位点的聚类结果,随着亚克隆数目的增加,某些亚克隆的变异频率较为接近,聚类性能会显著下降。当亚克隆数目为4时,聚类结果的准确率只有64.15%,直接影响单体型识别准确率。若聚类准确率为100%时,亚克隆单体型识别准确率均可达到99%以上。
|
图 3 在不同亚克隆数目下识别准确率分析 Fig.3 Analysis of recognition accuracy under different subclone numbers. |
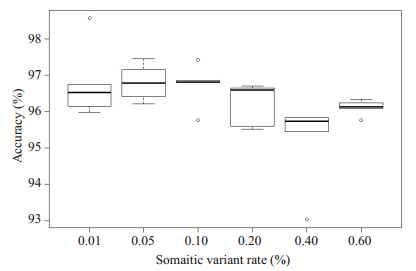
(4) 不同体细胞变异率下的性能分析。本组实验中包括了6种体细胞变异率,分别为0.01%、0.05%、0.1%、0.2%、0.4%、0.6%,如图 4所示,只要一条读段覆盖了两个以上的变异位点,单体型识别准确度受体细胞变异率影响较小,基本在95%以上。
|
图 4 不同体细胞变异率下识别准确率分析 Fig.4 Analysis of recognition accuracy under different somatic variant rates. |
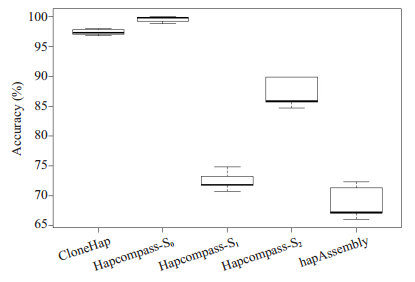
(5) 与其它工具对比:将CloneHap、Hapcompass[22]和hapAssembly[23]3种方法进行性能比较分析,分别将5种不同的染色体作为参考基因组序列,设定遗传变异率和体细胞变异率均为0.1%。包含3种亚克隆,其混合比例为S0:S1:S2=3:5:2(图 5)。
|
图 5 不同方法性能比较 Fig.5 Performance comparison of different methods. |
由于Hapcompass方法无法处理亚克隆混合数据,故HapCompass算法不适用于肿瘤中多级克隆单体型识别问题,仅对基础克隆的单体型识别较为精确,而对于其它克隆的单体型识别效果较差。hapAssembly是最近提出的一种基于最小化错误修正模型的单体型识别方法,在本组实验中使用命令sh hapAssembly2.sh 1example 0实现变异位点全部为杂合子的情况。从图可见,对于肿瘤克隆单体型识别问题,hapAssembly的识别准确率在70%左右,性能较CloneHap方法差。充分表明,CloneHap方法更适用于复杂克隆结构中的单体型识别问题。
3 讨论单体型识别是全基因组测序中的一个核心问题[24]。高通量测序技术为肿瘤学的研究与发展提供了必要的数据支撑和保障[25],尤其是第三代测序技术在读长与测序速度等方面具有明显优势,更利于肿瘤基因组序列组装及结构变异识别[26]。研究表明,肿瘤发展是一个动态的演变过程[27]。精确重构克隆单体型不仅有助于推断克隆演变模式及免疫微环境,而且有利于识别驱动变异及变异间的复杂关系,为临床辅助决策提供理论依据。
高通量测序数据的单体型组装极具计算挑战性,基于优化最小误差校正准则的方法属于NP难问题,在单体型组装中常采用次优的启发式策略[28]。本研究使用了一种改进的最大生成树算法,将肿瘤样本中识别的变异位点看作为图的顶点,将变异位点对之间的连接关系看作图的边,基于概率函数计算边的权值,将克隆单体型重构问题转换为无向图中搜索最大生成树问题,不仅简化了计算问题,而且在局部最优的基础上扩展最大生成树,确保识别结果最优。假设变异位点总数为n,最大生成树初始化的时间复杂度为O(n);求解图的最大生成树所用时间复杂度为O(n2),相比于贪婪算法的O(2n)级时间复杂度大幅降低,提高了算法性能。
对于某一患病个体,由于肿瘤发展进程不同,携带的克隆情况具有差异性且相对复杂,测序误差和复杂的变异位点使得已有的单体型组装方法在重构克隆单体型中受到局限,重构精准度降低。本研究遵循肿瘤克隆变异与继承原则,充分利用长读段的测序优势,逐级剥离克隆厚度的同时逐级扩展最大生成树,实现了肿瘤克隆单体型的层级式重构。此外,基于有连接关系的已知顶点状态进行综合评分确定单体型,提高其识别准确率。
本文所提方法在测序读段达到一定长度和覆盖度下,可以较为精确的重构肿瘤亚克隆单体型,其实现结果可以更好的了解肿瘤克隆演化过程,为肿瘤异质性研究提供理论依据。在下一步研究中,还需考虑扩展最大生成树时,精确实现亚克隆厚度剥离问题;考虑低覆盖度下,解决克隆单体型精确重构问题。
| [1] |
涂超峰, 綦鹏, 李夏雨, 等. 肿瘤异质性:精准医学需破解的难题[J]. 生物化学与生物物理进展, 2015, 42(10): 881-90. |
| [2] |
Easwaran H, Tsai HC, Baylin SB. Cancer epigenetics: tumor heterogeneity, plasticity of stem-like states, and drug resistance[J]. Mol Cell, 2014, 54(5): 716-27. DOI:10.1016/j.molcel.2014.05.015 |
| [3] |
耿彧, 赵仲孟, 刘建业, 等. 一种碱基精度的肿瘤基因组单体型异质性识别算法[J]. 西安交通大学学报, 2017, 51(6): 92-6. |
| [4] |
Aguiar D, Wong WS, Istrail S. Tumor haplotype assembly algorithms for cancer genomics[J]. Pac Symp Biocomput, 2014, 19(19): 3-14. |
| [5] |
Douglas JA, Boehnke M, Gillanders E, et al. Experimentally-derived haplotypes substantially increase the efficiency of linkage disequilibrium studies[J]. Nat Genet, 2001, 28(4): 361-4. DOI:10.1038/ng582 |
| [6] |
Browning SR, Browning BL. Haplotype phasing: existing methods and new developments[J]. Nat Rev Genet, 2011, 12(10): 703-14. DOI:10.1038/nrg3054 |
| [7] |
Lancia G, Bafna V, Istrail S, et al. SNPs problems, complexity and algorithms[C]//Proceedings of the 9th Annual European Symposium onAlgorithms, 2001: 182-93. http://www.springerlink.com/index/fkl6gj565rtdl44v.pdf
|
| [8] |
Lippert R, Schwartz R, Lancia G, et al. Algorithmic strategies for the single nucleotide polymorphism haplotype assembly problem[J]. Brief Bioinform, 2002, 3(1): 23-31. DOI:10.1093/bib/3.1.23 |
| [9] |
Wang Y, Feng E, Wang R. A clustering algorithm based on two distance functions for MEC model[J]. Comput Biol Chem, 2007, 31(2): 148-50. |
| [10] |
Bansal V, Halpern AL, Axelrod N, et al. An MCMC algorithm for haplotype assembly from whole-genome sequence data[J]. Genome Res, 2008, 18(8): 1336-46. DOI:10.1101/gr.077065.108 |
| [11] |
Matsumoto H, Kiryu H. MixSIH: a mixture model for single individual haplotyping[J]. BMC Genomics, 2013, 14(Suppl 2): S5. |
| [12] |
Wang RS, Wu LY, Li ZP, et al. Haplotype Reconstruction from SNP fragments by minimum error correction[J]. Bioinformatics, 2005, 21(10): 2456-62. DOI:10.1093/bioinformatics/bti352 |
| [13] |
Qian W, Yang Y, Yang N, et al. Particle swarm optimization for SNP haplotype reconstruction problem[J]. Appl Math Comput, 2008, 196(1): 266-72. |
| [14] |
Miller CA, White BS, Dees ND, et al. SciClone: inferring clonal architecture and tracking the spatial and temporal patterns of tumor evolution[J]. PLoS Comput Biol, 2014, 10(8): e1003665. DOI:10.1371/journal.pcbi.1003665 |
| [15] |
Ono Y, Asai K, Hamada M. PBSIM: PacBio reads simulator--toward accurate genome assembly[J]. Bioinformatics, 2013, 29(1): 119-21. |
| [16] |
Geng Y, Zhao Z, Xu M. TNSim: A tumor sequencing data simulator for incorporating clonality information[C]//. 2018: 371-82. http://link.springer.com/chapter/10.1007%2F978-3-319-95933-7_45
|
| [17] |
Chaisson MJ, Tesler G. Mapping single molecule sequencing reads using basic local alignment with successive refinement (BLASR): application and theory[J]. BMC Bioinformatics, 2012, 13(1): 238. DOI:10.1186/1471-2105-13-238 |
| [18] |
Kandoth C, Mclellan MD, Vandin F, et al. Mutational landscape and significance across 12 major cancer types[J]. Nature, 2013, 502(7471): 333-9. DOI:10.1038/nature12634 |
| [19] |
Wendl MC, Wilson RK. Aspects of coverage in medical DNA sequencing[J]. BMC Bioinformatics, 2008, 9(1): 239. DOI:10.1186/1471-2105-9-239 |
| [20] |
Ye C, Ma ZS. Sparc: a sparsity-based consensus algorithm for long erroneous sequencing reads[J]. Peer J, 2016, 4(24): e2016. |
| [21] |
Roth A, Ding J, Morin R, et al. JointSNVMix: a probabilistic model for accurate detection of somatic mutations in normal/tumour paired next-generation sequencing data[J]. Bioinformatics, 2012, 28(7): 907-13. DOI:10.1093/bioinformatics/bts053 |
| [22] |
Aguiar D, Istrail S. HapCompass: a fast cycle basis algorithm for accurate haplotype assembly of sequence data[J]. J Comput Biol, 2012, 19(6): 577-90. DOI:10.1089/cmb.2012.0084 |
| [23] |
Chen ZZ, Deng F, Wang L. Exact algorithms for haplotype assembly from whole-genome sequence data[J]. Bioinformatics, 2013, 29(16): 1938-45. DOI:10.1093/bioinformatics/btt349 |
| [24] |
Geraci F. Acomparison of several algorithms for the single individual SNP haplotyping Reconstruction problem[J]. Bioinformatics, 2010, 26(18): 2217-25. DOI:10.1093/bioinformatics/btq411 |
| [25] |
Gligorijević V, Pržulj N. Methods for biological data integration: perspectives and challenges[J]. J R Soc Interface, 2015, 12(112): 20150571. DOI:10.1098/rsif.2015.0571 |
| [26] |
Gordon D, Huddleston J, Chaisson MJ, et al. Long-read sequence assembly of the gorilla genome[J]. Science, 2016, 352(6281): aae0344. DOI:10.1126/science.aae0344 |
| [27] |
Hunter KW, Amin R, Deasy S, et al. Genetic insights into the morass of metastatic heterogeneity[J]. Nat Rev Cancer, 2018, 18(4): 211-23. DOI:10.1038/nrc.2017.126 |
| [28] |
Das S, Vikalo H. Optimal haplotype assembly via a branch-andbound algorithm[J]. IEEE Transactions on Molecular, Biological and Multi-Scale Communications, 2017, 3(1): 1-12. DOI:10.1109/TMBMC.2016.2640306 |
 2019, Vol. 39
2019, Vol. 39

