螺旋CT自问世以来,因其能够对人体进行快速三维扫描,且具有高时间分辨率、高空间分辨率等优点,已广泛应用于临床,包括辅助临床诊断,制定治疗计划,病情监测和评估等[1]。虽然螺旋CT扫描是一种非侵入式影像检查技术,但过量的X射线照射会增加病人出现遗传变异和组织癌变的风险[1-2]。降低螺旋CT检查的X射线辐射剂量是当前临床影像诊断的关切问题。稀疏角度扫描通过等间距减少球管旋转一周的曝光次数可以成倍降低螺旋CT扫描中的X射线辐射剂量,但是稀疏角度螺旋扫描采集到的投影数据具有不完备性,其重建图像不可避免会出现条形伪影与噪声,导致CT图像降质,进而影响临床诊断质量。如何解决螺旋CT中的稀疏角度重建问题,是当前CT成像领域的一个研究热点。
稀疏角度CT图像重建在数学上是一个病态的反问题求解。针对该问题,多种方法相继提出用于去除重建图像中稀疏角度引起的条形伪影和噪声,其大致可以分为以下三类:弦图数据插值、图像后处理以及迭代重建方法。弦图数据插值一般通过在CT投影域对弦图数据进行插补再进行解析重建[3-4],但插补得到的投影数据很难完整重现原有数据的细节信息,容易造成图像细节丢失。图像后处理方法则是在CT图像域采用降噪方法或者深度学习方法去除CT图像中的伪影和噪声[5-6],但稀疏角度引起的条形伪影近似于图像结构信息,难以得到良好的去除效果。而迭代重建方法是通过对投影数据进行统计建模,并引入图像自身的正则化约束实现重建图像的伪影抑制和噪声去除[7-10],能够提升重建图像质量。其中,基于全变分最小的凸集投影(TVPOCS)重建算法,通过引入全变分以描述CT图像一阶梯度的稀疏特性作为先验约束,较好解决了稀疏角度投影数据不完备性导致的图像重建问题[9-10];在此基础上,Sidky等[11]进行了算法改进,提出自适应梯度下降凸集投影算法ASD-POCS,通过引入自适应步长加速算法迭代收敛速度。但全变分(TV)模型基于分片光滑的理论假设,其各向同性边缘特性容易导致重建图像出现边缘过平滑和块状伪影现象。针对传统TV引起的过平滑和块状伪影问题多种改进算法相继提出[12-18]。其中一类改进策略是在原有TV模型中引入权重调节因子[12-13],如基于自适应加权TV最小化的凸集投影算法(AwTVPOCS),通过引入各向异性权重因子来解决TV边缘过平滑与块状伪影问题[12]。第二类改进策略是针对原有TV模型差分方向固定单一的缺点,提出自适应差分方向选择方法来提高重建图像边缘保持能力[14]。第三类改进策略是引入图像梯度的高阶信息[15-16],基于惩罚加权最小二乘(PWLS)重建框架,引入广义全变分(TGV)刻画CT图像的一阶梯度与二阶梯度结构稀疏特性,提出一种基于广义全变分最小的惩罚加权最小二乘(PWLS-TGV)稀疏角度CT重建算法,有效解决了原有TV模型的边缘过平滑与块状伪影问题[16]。然而,上述稀疏角度迭代重建算法是基于单层重组[19]的弦图数据进行螺旋CT重建,没有充分利用螺旋CT三维体数据相邻层之间的结构相关性与稀疏性。
鉴于此,本文从螺旋CT扫描成像几何的特点出发,将螺旋CT三维体数据看作张量,提出一种新的基于凸集投影的张量广义全变分最小(TTGV-POCS)的稀疏角度螺旋CT迭代重建算法。新方法通过分析螺旋重建图像的三维体数据空间结构稀疏特性和层间相关性,在POCS迭代重建框架下引入TTGV最小化约束以去除重建图像中的伪影与噪声。为验证TTGV-POCS算法的有效性,本文将常用稀疏角度迭代算法,如SIRT、ASD-POCS、AwTV-POCS等作为实验对比方法;同时本文选取了峰值信噪比(PSNR)和特征相似性参数(FSIM)两个定量指标对重建结果进行定量比较。
1 方法 1.1 螺旋CT成像几何螺旋CT锥束重建需要对其成像几何进行准确建模[20-21]。在螺旋CT系统中,螺旋CT扫描中,球管曝光旋转1周,扫描床匀速移动一个螺距的距离;通过连续数据采集,CT螺旋扫描方式1次连续采集可以获取三维容积数据。以扫描床为参考坐标,其螺旋状曝光轨迹在三维笛卡尔坐标系下可以描述为:
| $ y(\lambda)=\left(R \cos \lambda, R \sin \lambda, \frac{h}{2 \pi} \lambda\right)^{T} $ | (1) |
其中,λ表示为球管旋转角度,λ ∈[0, 2n],n为π的倍数;R表示球管到螺旋旋转中心的距离;h表示球管旋转一周时扫描床移动的距离。区别于圆周扫描,螺旋CT每曝光1次,扫描床在z轴方向就移动$\frac{h}{2 \pi}$的距离。螺旋几何和圆周几何的扫描轨迹示意图(图 1)。螺旋CT的前投影操作为:
| $ D(y(\lambda), \beta)=\int\limits_{0}^{\infty} f(y(\lambda)+t \beta) d t $ | (2) |
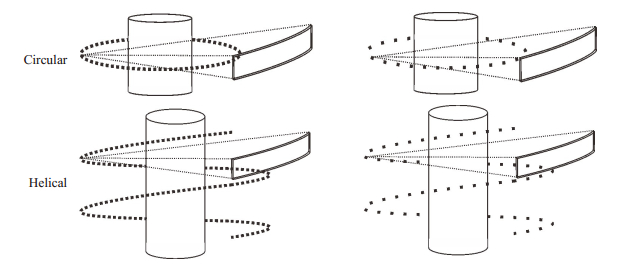
|
图 1 圆周几何和螺旋几何稀疏角度扫描轨迹示意图 Fig.1 Schematic diagram of sparse-view scan of circular geometry and helical geometry. The left column is the full-view scan, and the right column is the sparse-view scan. |
其中,D(y(λ), β)表示为螺旋CT探测器当前λ角度下扫描获得的投影数据。f (x)表示为人体在同一坐标系下的位置,β表示为穿过像素点X射线的单位向量,通过y(λ) + tβ就可确定某一时刻射线穿过人体的位置。
1.2 张量广义全变分(TTGV)TGV是Bredies等[22]在2010年第1次提出的数学去噪模型,用于描述图像差分的高阶特性。Chen等[23]将TGV应用于CBCT圆周几何并结合增广拉格朗日框架来解决圆周几何稀疏角度扫描下的TV过平滑和阶梯伪影问题。将张量TGV应用于心肌灌注CT(MPCT)迭代重建(PLWS-TTGV)来提升定量心肌灌注成像质量[24]。TTGV可以看作TGV模型在第三维上的扩展,其二阶TTGV模型可以表示为:
| $T T G V_{a}^{2}(U)=\mathop {\min }\limits_V \alpha_{1}|\nabla U-V|+\alpha_{0}|\varepsilon V| $ | (3) |
其中,U ∈ RM × N × S为目标图像,V表示图像的梯度。∇表示对三维目标图像的离散操作,ε = 0.5(∇ + ∇T)表示三维图像的对称梯度偏导操作。α0和α1分别表示一阶偏导和二阶偏导的权重因子,在平滑区域εV值接近于零,最小化TTGV模型则∇U接近于V,能够很好的抑制图像产生阶梯伪影。相反,对于图像边缘区域,εV值很大,最小化TTGV模型会使梯度图像接近于零,因此能够很好的保持细节和边缘信息。
1.3 张量广义全变分-凸集投影(TTGV-POCS)借鉴ASD-POCS模型中的凸集投影操作[11],基于POCS的TTGV最小化模型可以表示为:
| $ \mathop {\min }\limits_{\mu \ge 0} \|\mu\|_{T T G V} \ subject \ to\ |y-A \mu| \leq \delta $ | (4) |
其中,y = (y1, y2, …, yM)T表示扫描得到的弦图数据,μ = (μ1, μ2, …, μN)T表示三维重建图像的衰减系数值。Aμ表示螺旋CT中的前投影操作,A表示M × N大小的稀疏扫描系统矩阵。δ表示前投影中实际物理因素导致的误差因子。||μ||TTGV表示对重建图像的张量全变分操作。
为解决式(4)条件约束最小化问题,目标方程的优化求解可以通过两步交替循环操作实现,具体为POCS非负约束和TTGV最小化操作。
TTGV-POCS稀疏角度螺旋CT重建算法主要步骤可以归纳为:
Step1.获取稀疏角度投影数据并设置初始值,本文以wFBP解析重建结果作为初始图像;
Step2. POCS迭代采用SIRT联立迭代重建实现。目的使图像满足一致性约束,并确保图像衰减系数为非负值;
Step3.对非负约束后的迭代结果做TTGV最小化约束。利用三维图像广义全变分约束最小化去除条形伪影和噪声并保持边缘细节。
Step4.设置迭代终止条件,循环执行2和3步骤。当满足终止条件时停止迭代,得到稀疏角度重建最优图像。
1.4 实验数据为验证所提TTGV-POCS方法在稀疏角度螺旋CT重建中的有效性和准确性,本文利用XCAT体模仿真数据和真实病人数据进行实验。实验中,螺旋CT成像几何采用了西门子SOMATOM Definition as+CT设备成像几何,具体参数为:X射线球管旋转一周的球管曝光次数为1152,探测器排数为64、通道数为736,球管到旋转中心的距离为595 mm,球管到探测器的距离为1085.6 mm,螺距为0.6。其中XCAT体模数据参考文献[25]中的仿真方法得到,其中X射线入射光子数设置为7 × 105,并在对数变换前加入泊松和高斯混合噪声以仿真真实螺旋扫描情况[26];真实病人数据来自mayo医疗的开源数据测试集[27] (https://www.aapm.org/GrandChallenge/LowDoseCT/),采集自西门子SOMATOM Definition as+ CT设备,管电压120 kVp,层厚1 mm。稀疏角度扫描数据是通过对全角度扫描数据进行8倍等间距降采样得到,即球管旋转一周的曝光次数由1152降低为144。
1.5 定量评价指标为了定量评价所提算法的性能,本文采用了峰值信噪比(PSNR)和特征相似性(FSIM)[28]对稀疏角度螺旋CT重建结果进行定量分析,其具体定义如下:
| $P S N R=10 \log _{10}\left(\frac{\left(2^{n}-1\right)^{2}}{\frac{1}{h w} \sum\limits_{i=0}^{n-1} \sum\limits_{j=0}^{w-1}\|I(i, j)-K(i, j)\|^{2}}\right) $ | (5) |
其中,n表示图像的保存位数,灰度图像n为8。h和w分别表示图像的长和宽。除数部分为均方根误差(MSE)。K表示量化输入的衰减系数重建图像。PSNR用于测量最大信号和背景噪声强度的比值,PSNR值越大,图像去除噪声越明显。
| $ F S I M=\frac{\sum\nolimits_{x \in \Omega} S_{L}(x) \cdot P C_{m}(x)}{\sum\nolimits_{x \in \Omega} P C_{m}(x)} $ | (6) |
其中,SL(x) =[SPC(x)]α[SG(x)]β表示相位一致性和梯度的相似性。$P{C_m}(x) = \max \left({{{\mathop {PC}\limits^ \vee }_1}(x), {{\mathop {PC}\limits^ \vee }_1}(x)} \right)$表示图像的显著相位一致性。Ω表示图像三维空间域。FSIM用来衡量两幅图像的结构相似性,当指标值越接近1,表示两幅图像特征越相似。
2 结果为了验证所提TTGV-POCS算法的性能,本文将所提算法与wFBP解析重建算法[29-30]、SIRT、ASD-POCS和AwTV-POCS进行了比较,分别从定性和定量两方面进行了结果对比。结果部分展示了XCAT数字体模和病人胸腹部实验结果。
2.1 XCAT数据实验结果图 2为XCAT体模仿真数据不同重建算法对应的稀疏角度螺旋CT重建结果,每种算法分别展示了3个不同切面的重建图像,中间为横断面,右侧为矢状面,下方为冠状面。图 2A和图 2B分别为全角度wFBP解析重建图像和稀疏角度wFBP解析重建结果,图 2C-F分别为SIRT、ASD-POCS、AwTV-POCS和TTGV-POCS重建结果。图像显示窗宽均为600,窗位均为40。SIRT迭代步数为220。从图 2F重建结果可以看出,如红色和黄色箭头所示,TTGV-POCS在体模数据中能够很好的去除稀疏角度引起的伪影并保持图像边缘细节。表 1为图 2中XCAT体模仿真数据不同重建算法重建结果的PSNR测量值;表 2为图 2中XCAT体模仿真数据不同重建算法重建结果的FSIM测量值。每个表中分别给出了三维图像不同断面的测量结果。
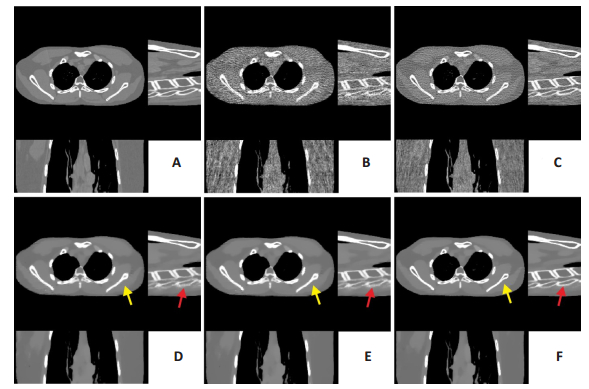
|
图 2 XCAT体模稀疏角度迭代重建算法三维结果对比 Fig.2 Comparison of three-dimensional results of iterative reconstruction algorithm based on XCAT phantom data. A: wFBP reconstruction with full-views projection; B: wFBP reconstruction with sparse-views projection; C: SIRT; D: ASD-POCS; E: AwTV-POCS; F: TTGV-POCS. |
| 表 1 XCAT体模数据不同重建方法PSNR结果对比 Tab.1 Comparison of PSNR results of different reconstruction methods based on XCAT data |
| 表 2 XCAT体模数据不同重建方法FSIM结果对比 Tab.2 Comparison of FSIM results of different reconstruction methods based on XCAT data |
图 3为mayo医疗病人上腹部数据不同重建算法对应的稀疏角度螺旋CT重建结果。病人数据中展示了上腹部横断面、冠状面和矢状面图像结果。图 3A、B分别为机器解析重建和稀疏角度wFBP解析重建结果。图 3C~F分别为SIRT、ASD-POCS、AwTV-POCS和TTGVPOCS重建结果。图像显示窗宽均为600,窗位均为40。从病人上腹部结果可以看出,如红色和黄色箭头所示,虽然对比方法和TTGV-POCS方法都有效的去除了稀疏角度引起的伪影,但是在噪声抑制方面,对比方法仍然存在局部噪声,TTGV-POCS能够均匀的去除噪声。从表 3、4分别为图 3中病人数据不同重建算法重建结果3个切面的PSNR、FSIM测量值。
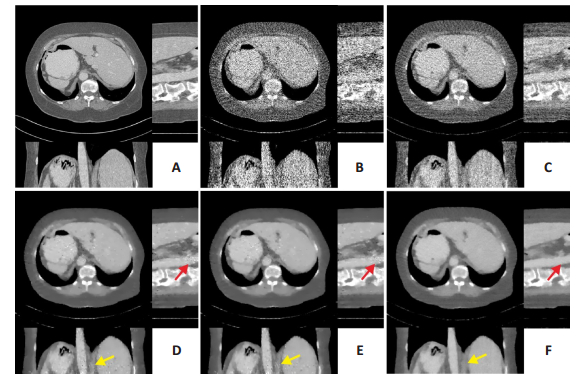
|
图 3 病人上腹部数据稀疏角度重建算法三维结果对比 Fig.3 Three-dimensional results of iterative reconstruction algorithms based on patient epigastrium projection. A: Machine analytic reconstruction result; B: wFBP reconstruction with sparse-views projection; C: SIRT; D: ASD-POCS; E: AwTV-POCS; F: TTGV-POCS. |
| 表 3 病人上腹部数据不同重建方法PSNR结果对比 Tab.3 Comparison of PSNR results of different reconstruction methods based on patient epigastrium data |
| 表 4 病人上腹部数据不同重建方法FSIM结果对比 Tab.4 Comparison of FSIM results of different reconstruction methods based on patient epigastrium data |
图 4为mayo医疗病人胸部数据不同重建算法对应的稀疏角度螺旋CT重建结果。图 4A、B分别为机器解析重建和稀疏角度wFBP解析重建结果。图 4C~F分别为SIRT、ASD-POCS、AwTV-POCS和TTGV-POCS重建结果。图像显示窗宽均为1500,窗位均为-400。病人胸部图像中存在稀疏角度引起的噪声和伪影。从病人胸部结果图 4F中可以看出,如红色和黄色箭头所示,对比方法和TTGV-POCS都很好的去除了伪影和噪声,但在图像细节保持方面,TTGV-POCS保持了胸部血管末端细节和组织结构纹理信息。表 5、6分别为图 4中病人数据不同重建算法重建结果3个切面的PSNR、FSIM测量值。
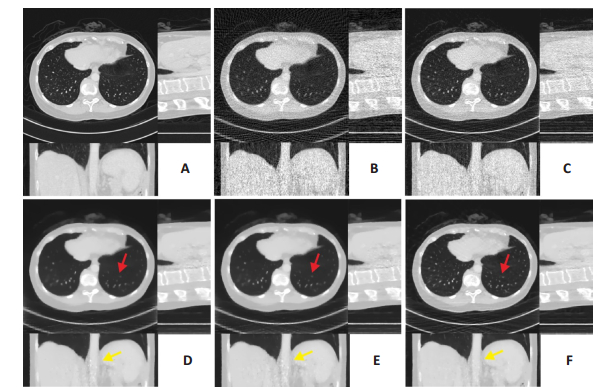
|
图 4 病人胸部数据稀疏角度重建算法三维结果对比 Fig.4 Three-dimensional results of iterative reconstruction algorithms based on patient chest projection. A: Machine analytic reconstruction result; B: wFBP reconstruction with sparse-views projection; C: SIRT; D: ASD-POCS; E: AwTV-POCS; F: TTGV-POCS. |
| 表 5 病人胸部数据不同重建方法PSNR结果对比 Tab.5 Comparison of PSNR results of different reconstruction methods based on patient chest data |
| 表 6 病人胸部数据不同重建方法FSIM结果对比 Tab.6 Comparison of FSIM results of different reconstruction methods based on patient chest data |
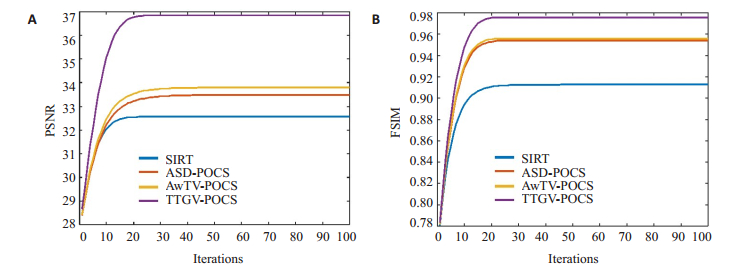
为了比较不同重建算法的收敛性,本文选取了XCAT体模数据前100次稀疏角度迭代结果横断面图像对应的PSNR与FSIM测量值进行比较。图 5为对应的PSNR与FSIM收敛曲线图。
|
图 5 XCAT体模实验前100次迭代横断面收敛曲线结果 Fig.5 Convergence curve of XCAT phantom experiment transverse section based on 144 views projection with 100 iterations. A: PSNR curves for different reconstruction methods; B: FSIM curves for different reconstruction methods. |
本文实验基于Matlab2016b软件实现,计算机配置为Xeon(R) CPU E5-2643v@3.40 GHz,并使用Tesla k40显卡加速。以XCAT体模实验为例,在迭代25步时达到收敛情况下重建144层图像,TTGV-POCS运行时间为重建每层所需时间为1.7847 s。wFBP为解析重建结果,运行时间为重建每层0.125 s,其重建速度接近机器重建结果。对比方法SIRT、ASD-POCS和AwTV-POCS重建每层的运行时间分别为0.6944、1.1389、1.3334 s。
3 讨论基于TV最小化的稀疏角度螺旋CT重建能够去除条形伪影和噪声,但是容易导致重建图像过平滑或者引入块状伪影。针对该问题,现有的改进方法是在原有的TV模型中引入权重因子或增加梯度方向以保持图像边缘信息。例如,基于二维图像的梯度信息引入各向异性权重因子,从而提高图像保持边缘的能力[12-13];将二维图像的梯度差分由四邻域方向增加到八邻域方向的差分计算,提高图像的细节保持能力[14]。然而这些方法均基于单层重组的弦图数据进行图像重建,先验约束只考虑了二维图像数据相邻像素间梯度差分信息,没有充分利用螺旋CT三维体数据的层间信息。针对稀疏角度螺旋CT重建,本文利用其三维体数据的特点,将螺旋CT图像数据看作张量,提出TTGV-POCS算法用于稀疏角度螺旋CT重建。TTGV充分利用张量数据一阶梯度与二阶梯度的空间结构稀疏特性和层间相关性,能够更好的保持图像边缘和去除块状伪影。结合POCS凸集投影迭代框架[10],本文利用循环交替的方式来优化目标方程。为了评价TTGV-POCS算法的准确性和有效性,本文在XCAT仿真数据和病人扫描数据下进行实验验证。
在XCAT体模实验中,对比图 2中不同重建方法稀疏角度重建结果,图 2B中稀疏角度解析重建结果存在大量的噪声和伪影,而迭代重建算法对应的结果在3个不同断面上对噪声和伪影均有较好的抑制,并能较好保持图像细节;相比SIRT算法,ASD-POCS、AwTV-POCS、TTGV-POCS通过引入先验约束对图像噪声和条形伪影取得了更好的抑制效果,但在冠状面和矢状面可以注意到,ASD-POCS与AwTV-POCS的图像细节和边缘结构信息有部分丢失;与全角度解析重建结果相比,TTGV-POCS在去除条形伪影和噪声的同时,能够更好的保持图像的边缘细节,更接近全角度重建结果。从表 1和表 2可以看出,SIRT算法的PSNR参数指标虽然低于ASD-POCS和AwTV-POCS迭代算法,但是SIRT的FSIM特征相似性指标高于ASD-POCS和AwTV-POCS迭代算法,说明TV和AwTV先验约束在抑制噪声与伪影的同时均造成了图像边缘等细节信息的丢失,而TTGV-POCS算法通过充分利用螺旋CT数据的高阶梯度信息与层间相关信息,能在抑制噪声与伪影的同时有效保持图像细节,具有更优的PSNR和FSIM指标。为分析TTGV-POCS迭代算法的收敛性,图 5为XCAT体模稀疏角度重建在迭代次数设置为100时横断面的PSNR和FSIM收敛曲线结果。从图 5可以看出,4种迭代重建算法均具有良好的算法收敛性,迭代25步左右均趋近于收敛,而TTGV-POCS相比其他3种算法具有更高的PSNR和FSIM值。
在病人数据实验中,从图 3和图 4稀疏角度解析重建结果可以看出,病人稀疏角度扫描中存在较强的条形伪影和非均匀分布的噪声。通过SIRT方法可以抑制部分稀疏角度伪影和降低噪声水平。ASD-POCS和AwTV-POCS虽然能够去除大部分伪影和噪声,但从3个切面可以看出,局部区域仍然还存在较强的噪声并且出现块状伪影。在不损失分辨率的前提下,TTGVPOCS能够均匀的去除噪声。从图 3可以看出,在病人数据的稀疏角度螺旋CT中,ASD-POCS、AwTV-POCS和TTGV-POCS都能很好的去除稀疏角度伪影。但在噪声抑制方面,TTGV-POCS优于SIRT、ASD-POCS、AwTV-POCS算法。从表中也可以看出,在PSNR与FSIM方面,迭代重建结果明显优于解析重建结果,而TTGV-POCS相比ASD-POCS和AwTV-POCS具有更好的表现。
同时,本研究还存在一些不足。由于目前临床实验数据有限,本文未针对不同剂量、不同部位的临床数据进行算法评估。在未来工作中将进一步补充采集临床数据,并引入临床医生评分对重建结果进行评价以及实验结果的统计学分析;目前TTGV-POCS算法的重建速度未能满足临床需求,未来工作中将通过算法优化和硬件提升进行解决。
综上所述,TTGV-POCS算法通过结合TTGV模型和螺旋CT三维体数据特点,具有良好的噪声与伪影抑制及图像边缘保持效果,可有效改善稀疏角度螺旋CT重建图像质量,降低螺旋CT检查辐射剂量,展现出良好的临床应用潜力,将更好服务于临床影像诊断。
| [1] |
莫家彬, 贾红明, 李苒光, 等. 低剂量螺旋CT扫描用于早期肺癌诊断临床分析[J]. 临床肺科杂志, 2013, 18(9): 1713-4. DOI:10.3969/j.issn.1009-6663.2013.09.085 |
| [2] |
周清华, 范亚光, 王颖, 等. 中国肺癌低剂量螺旋CT筛查指南(2018年版)[J]. 中国肺癌杂志, 2018, 21(2): 67-75. |
| [3] |
Bertram M, Wiegert J, Schafer D, et al. Directional view interpolation for compensation of sparse angular sampling in cone-beam CT[J]. IEEE Trans Med Imaging, 2009, 28(7): 1011-22. DOI:10.1109/TMI.2008.2011550 |
| [4] |
Kim D, Park SW, Kim DH, et al. Feasibility of sinogram Reconstruction based on inpainting method with decomposed sinusoid-like curve (S-curve) using total variation (TV) noise reduction algorithm in computed tomography (CT) imaging system: A simulation study[J]. Optik (Stuttg), 2018, 161(11): 270-7. |
| [5] |
Zhang Z, Liang X, Dong X, et al. A Sparse-View CT Reconstruction method based on combination of DenseNet and deconvolution[J]. IEEE Trans Med Imaging, 2018, 37(6): 1407-17. DOI:10.1109/TMI.2018.2823338 |
| [6] |
Bittencourt MS, Schmidt B, Seltmann M, et al. Iterative Reconstruction in image space (IRIS) in cardiac computed tomography: initial experience[J]. Int J Cardiovasc Imaging, 2011, 27(7): 1081-7. DOI:10.1007/s10554-010-9756-3 |
| [7] |
Bian ZY, Ma JH, Tian LL, et al. Penalized weighted Alpha-Divergence approach to sinogram restoration for Low-Dose x-ray computed tomography[C] //2012 IEEE Nuclear Science Symposium And Medical Imaging Conference Record (NSS/MIC), 2012: 3675-8.
|
| [8] |
Ma J, Huang J, Feng Q, et al. Low-dose computed tomography image restoration using previous normal-dose scan[J]. Med Phys, 2011, 38(10): 5713-31. DOI:10.1118/1.3638125 |
| [9] |
Li RD, Osher S, fatemi E. nonlinear total variation based noise removal algorithms[J]. Physica D, 1992, 60(4): 259-68. |
| [10] |
Sidky E, Kao C, Pan X. accurate image Reconstruction from fewviews and limited-angle data in divergent beam CT[J]. J Xray Sci Technol, 2006, 14(2): 119-39. |
| [11] |
Sidky EY, Pan X. Image Reconstruction in circular cone-beam computed tomography by constrained, total-variation minimization[J]. Phys Med Biol, 2008, 53(17): 4777-807. DOI:10.1088/0031-9155/53/17/021 |
| [12] |
Liu Y, Ma J, Fan Y, et al. Adaptive-weighted total variation minimization for sparse data toward low-dose x-ray computed tomography image Reconstruction[J]. Phys Med Biol, 2012, 57(23): 7923-56. DOI:10.1088/0031-9155/57/23/7923 |
| [13] |
Wang Y, Qi Z. A new adaptive-weighted total variation sparse-view computed tomography image reconstruction with local improved gradient information[J]. J Xray Sci Technol, 2018, 26(6): 957-75. |
| [14] |
Qu ZY, Zhao XJ, Pan JX, et al. Sparse-view CT Reconstruction based on gradient directional total variation[J]. Measurement Science and Technology, 2019, 30(5): 11-23. |
| [15] |
Niu S, Huang J, Bian Z, et al. Iterative Reconstruction for sparseview x-ray CT using alpha-divergence constrained total generalized variation minimization[J]. J Xray Sci Technol, 2017, 25(4): 673-88. |
| [16] |
Niu S, Gao Y, Bian Z, et al. Sparse-view x-ray CT Reconstruction via total generalized variation regularization[J]. Phys Med Biol, 2014, 59(12): 2997-3017. DOI:10.1088/0031-9155/59/12/2997 |
| [17] |
Gao Y, Bian Z, Huang J, et al. Low-dose X-ray computed tomography image Reconstruction with a combined low-mAs and sparse-view protocol[J]. Opt Express, 2014, 22(12): 15190-210. DOI:10.1364/OE.22.015190 |
| [18] |
Chen GH, Tang J, Leng S. Prior image constrained compressed sensing (PICCS): a method to accurately reconstruct dynamic CT images from highly undersampled projection data sets[J]. Med Phys, 2008, 35(2): 660-3. DOI:10.1118/1.2836423 |
| [19] |
Noo F, Defrise M, Clackdoyle R. Single-slice rebinning method for helical cone-beam CT[J]. Phys Med Biol, 1999, 44(2): 561-70. DOI:10.1088/0031-9155/44/2/019 |
| [20] |
Thibault JB, Sauer KD, Bouman CA, et al. A three-dimensional statistical approach to improved image quality for multislice helical CT[J]. Med Phys, 2007, 34(11): 4526-44. DOI:10.1118/1.2789499 |
| [21] |
Yan XH, Leahy RM. Cone beam tomography with circular, elliptical and spiral orbits[J]. Phys Med Biol, 1992, 37(3): 493-506. |
| [22] |
Bredies K, Kunisch K, Pock T. Total generalized variation[J]. SIAM J Imaging Sci, 2010, 3(3): 492-526. DOI:10.1137/090769521 |
| [23] |
Chen J, Wang L, Yan B, et al. Efficient and robust 3D CT image Reconstruction based on total generalized variation regularization using the alternating direction method[J]. J Xray Sci Technol, 2015, 23(6): 683-99. |
| [24] |
Gu C, Zeng D, Lin J, et al. Promote quantitative ischemia imaging via myocardial perfusion CT iterative reconstruction with tensor total generalized variation regularization[J]. Phys Med Biol, 2018, 63(12): 125009. DOI:10.1088/1361-6560/aac7bd |
| [25] |
Zheng X, Ravishankar S, Long Y, et al. PWLS-ULTRA: an efficient clustering and Learning-Based approach for Low-Dose 3D CT image Reconstruction[J]. IEEE Trans Med Imaging, 2018, 37(6): 1498-510. DOI:10.1109/TMI.2018.2832007 |
| [26] |
Ma JH, Liang ZR, Fan Y, et al. Variance analysis of x-ray CT sinograms in the presence of electronic noise background[J]. Med Phys, 2012, 39(7): 4051-65. |
| [27] |
Flohr TG, Stierstorfer K, Ulzheimer S, et al. Image Reconstruction and image quality evaluation for a 64-slice CT scanner with zflying focal spot[J]. Med Phys, 2005, 32(8): 2536-47. DOI:10.1118/1.1949787 |
| [28] |
Zhang L, Zhang L, Mou X, et al. FSIM: a feature similarity index for image quality assessment[J]. IEEE Trans Image Process, 2011, 20(8): 2378-86. DOI:10.1109/TIP.2011.2109730 |
| [29] |
Stierstorfer K, Rauscher A, Boese J, et al. Weighted FBP - a simple approximate 3D FBP algorithm for multislice spiral CT with good dose usage for arbitrary pitch[J]. Phys Med Biol, 2004, 49(11): 2209-18. DOI:10.1088/0031-9155/49/11/007 |
| [30] |
Hoffman J, Young S, Noo F, et al. Technical Note: FreeCT_wFBP: A robust, efficient, open-source implementation of weighted filtered backprojection for helical, fan-beam CT[J]. Med Phys, 2016, 43(3): 1411-20. DOI:10.1118/1.4941953 |
 2019, Vol. 39
2019, Vol. 39

