2. 南方医科大学 南方医院口腔科,广东 广州 510515;
3. 中山大学光华口腔医学院·附属口腔医院口腔颌面头颈肿瘤外科//广东省口腔医学重点实验室,广东 广州 510055
2. Department of Stomatology, Nanfang Hospital, Southern Medical University, Guangzhou 510515, China;
3. Department of Oral and Maxillofacial Surgery, Guanghua School of Stomatology, Hospital of Stomatology Affiliated to Sun Yat-sen University, Guangdong Provincial Key Laboratory of Stomatology, Guangzhou 510055, China
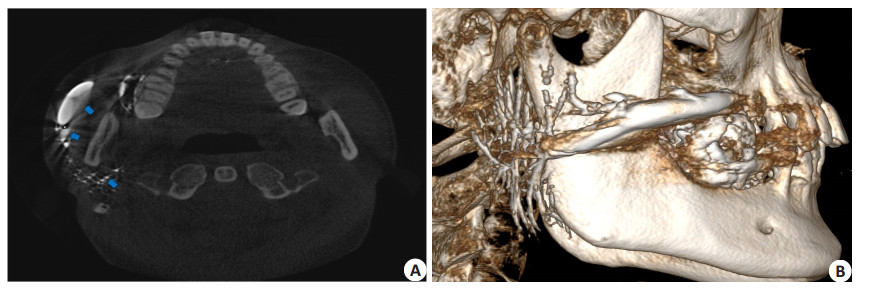
腮腺导管的口径、尺寸和角度都与临床相关, 它可以表示病理过程, 研究腮腺导管的形态学特征对腮腺类疾病的诊断和治疗有重要意义[1-4]。由于临床图像数据中, 存在噪声、灰度不均匀、边界不清晰等不良因素, 导致传统的分割方法在分割图像时出现分割结果边界不连续、不光滑、不能很好地逼近图像真实边界的情况。图 1所示, (A)为患者左侧腮腺注射造影剂后5 min内行CBCT检查的扫描结果, (B)为对应的RadiAnt软件重建结果, 从图中蓝色箭头所指区域不难看出, 导管边界模糊, 图像灰度不均匀, 并且存在大量细小颗粒目标, 给实际分割带来了巨大的挑战。
|
图 1 (A) 腮腺导管CBCT扫描结果 (B) 腮腺导管 RadiAnt软件重建结果 Fig.1 (A) CBCT scan results of the parotid duct; (B) RadiAnt Software reconstruction results of the parotid duct. |
在图像分割领域, 活动轮廓模型(ACM)因其能够很好地适应拓扑结构的变化以及在平滑方面优越的表现, 在图像处理和计算机视觉领域被广泛应用[5-11], 其基本原理是初始化一条轮廓线, 作为一个更高维度函数的零水平集, 然后通过最小化能量函数来驱动曲线演化, 不断逼近图像的真实边界。现有的活动轮廓模型可根据其分割原理分为两类:基于边缘的活动轮廓模型[12~16]和基于区域的活动轮廓模型[17-21]。其中, 基于边缘的活动轮廓模型是利用图像的梯度信息来约束曲线演化, 使曲线在到达图像边界处停止, 缺点在于对边界敏感; 基于区域的活动轮廓模型依靠一定的区域描述符来引导活动轮廓的运动, 其中较经典的是Chan等[17]提出的C-V模型, 该模型最初被提出是基于将图像看成一个分段常数函数的假设, 用来解决Mumford-Shah[22-23]问题, 但其仅考虑了全局区域的灰度信息, 因此对于细节丰富的腮腺导管图像, 也不能实现准确地分割。
为了克服全局区域不能很好表达图像信息这一缺点, Li等[24-26]在能量泛函中引入了图像的局部信息, 提出了基于局部区域的LBF模型, 对不均匀图像的处理也能够取得很好的效果。但该模型对参数敏感, 在处理噪声和边界模糊图像时, 不能自适应地收敛至正确的图像边缘。在此之后, Niu等[27]提出了对噪声具有较强鲁棒性的RLSF模型, 然而该方法也未解决对参数敏感这一问题, 并且在处理具有丰富灰度级和弱梯度边缘图像时也有一定的缺陷。
考虑到图像内外局部灰度的差异, 我们提出了一种新的快速自适应活动轮廓模型来解决这些限制, 相比现有的模型, 本文做出了以下贡献:第一, 本文首次将轮廓内外局部灰度的差异加入至能量泛函, 当两者灰度差异很大时, 即演化曲线逼近图像边缘时, 减缓曲线演化速度, 反之, 加速曲线演化; 第二, 本文应用邻域平均算子计算局部邻域灰度均值, 在表达局部图像信息的同时, 又对图像进行了一定的平滑, 消除了部分噪声和灰度不均匀对分割结果的影响。第三, 本文将内外轮廓局部邻域的匀质性差异代替λ1、λ2作为内、外局部能量参数值的控制项, 解决了模型对参数敏感这一问题, 同时还提高了曲线的演化效率。
1 LBF模型局部二值拟合模型(LBF模型)的提出是用于解决在对灰度不均匀图像分割上遇到的难题, 它是通过引入高斯核函数来实现的。给定一幅图像I (x)(x ∈ Ω), Ω为图像域, 对于图像域Ω中每个点x, 其对应的能量函数为:
| $ \begin{array}{l} {E^{LBF}}\left( {\phi ,{f_1},{f_2}} \right) = \mu \int_\Omega {\frac{1}{2}{{\left( {\left| {\nabla \phi \left( x \right)} \right| - 1} \right)}^2}dx} + \\ v\int_\Omega {\left| {\nabla {H_\varepsilon }\left( {\phi \left( x \right)} \right)} \right|dx} \\ + {\lambda _1}\int_\Omega {\int_\Omega {{K_\sigma }\left( {x - y} \right){{\left| {I\left( y \right) - {f_1}\left( x \right)} \right|}^2}{H_\varepsilon }\left( {\phi \left( y \right)} \right){\rm{d}}y{\rm{d}}x} } \\ + {\lambda _2}\int_\Omega {\int_\Omega {{K_\sigma }\left( {x - y} \right){{\left| {I\left( y \right) - {f_2}\left( x \right)} \right|}^2}} } \\ \left( {1 - {H_\varepsilon }\left( {\phi \left( y \right)} \right)} \right){\rm{d}}y{\rm{d}}x \end{array} $ | (1) |
其中, μ, v, λ1, λ2是固定的正数, ϕ为水平集函数, 第一项是距离惩罚项, 该项是为了保证每次曲线演化之后的水平集函数是符号距离函数[28], 使水平集函数在曲线演化过程中无需重新初始化; 第二项是演化曲线长度约束项, 该项的作用是调节曲线长度; 第三项和第四项分别代表轮廓内外部能量, kσ(x)为高斯核函数, f1(x)和f2(x)对应轮廓内外点x的局部灰度均值, Hε(ϕ(x))和δε(ϕ(x))分别是Heaviside函数和Dirac函数, 定义如下:
| $ {H_\varepsilon }\left( {\phi \left( x \right)} \right) = \frac{1}{2}\left( {1 + \frac{2}{{\rm{ \mathsf{ π} }}}\arctan \left( {\frac{{\phi \left( x \right)}}{\varepsilon }} \right)} \right) $ | (2) |
| $ {\delta _\varepsilon }\left( {\phi \left( x \right)} \right) = \frac{1}{{\rm{ \mathsf{ π} }}} \cdot \frac{\varepsilon }{{{\varepsilon ^2} + {{\left( {\phi \left( x \right)} \right)}^2}}} $ | (3) |
LBF模型相比于传统模型, 其突出贡献在于解决了水平集函数重新初始化的问题, 加快了水平集演化速度, 并且该模型通过高斯核函数将局部灰度均值引入至能量泛函, 增强了模型在处理灰度不均匀图像和噪声图像上的鲁棒性。然而对于同时拥有噪声、灰度不均匀、边界不清晰等缺点的腮腺导管图像, 该模型很难满足快速又准确地分割出目标区域的要求。考虑到局部灰度均值并不能很好的表达一个局部区域的完整信息, 因此本文引入了局部灰度差异信息, 同时将两者用来表达局部区域的灰度信息, 提高了分割效率。
2 基于局部灰度差异的快速自适应活动轮廓模型(FALD) 2.1 邻域局部相似因子本文在处理邻域信息时引入了两种不同邻域大小的局部相似因子用来减少噪声的影响以及保留图像细节。实际上, 对于给定的一幅图像, 其每个像素点的灰度和与之对应邻域的灰度是相似的, 在本文算法中, 每个中心点对应的邻域由两部分构成:大小为p*p的方形邻域和半径为r的圆形邻域(一般r > p), 我们将图像中心点x对应的能量函数定义如下:
| $ FALD\left( {x,LM\left( x \right)} \right) = \int_{\left( {y \in {N_x}} \right) \ne x} {\frac{{{{\left| {I\left( y \right) - LM\left( x \right)} \right|}^2}}}{{D\left( {x,y} \right)}}{\rm{d}}y} $ | (4) |
其中, Nx表示中心点x的局部方形邻域, y是局部邻域内的像素点, D (x, y)表示像素点y与中心点x之间的欧氏距离。由此可见, 邻域内像素点的权重是由其对应中心点欧氏距离来表达, 这是为了控制减少噪声影响与保留图像细节之间的平衡。LM (x)表示中心点x的邻域均值, 其被定义为:
| $ LM\left( x \right) = \frac{{\int_\Omega {R\left( {x,y} \right)I\left( y \right){\rm{d}}y} }}{{\int_\Omega {R\left( {x,y} \right){\rm{d}}y} }} $ | (5) |
R (x, y)为圆形邻域权重因子, 用于计算中心点x圆形邻域中像素点y的权重值, 其定义如下:
| $ R\left( {x,y} \right) = \left\{ \begin{array}{l} \frac{1}{N},D\left( {x,y} \right) \le r\\ 0,\;\;\;\;\;o{\rm{th}}er \end{array} \right. $ | (6) |
其中, N表示中心点x的局部圆形邻域中像素点的个数(包含x点), D (x, y)表示该邻域内的像素点y与中心点x之间的欧氏距离, r是局部圆形邻域的半径。由上述公式(6)可以看出, 计算圆形邻域权重值时, 采用的是平滑算子, 一定程度上也控制了噪声和不均匀灰度带来的影响。
2.2 局部灰度差异统计学上, 均值和方差是表达数据统计特性的两个重要统计量。在本文算法中, 我们将轮廓内外局部灰度差异用这两部分来表示:均值差异和方差差异。其中局部灰度均值差异指轮廓内外局部邻域间像素灰度值的平均差异, 它可以反映轮廓内外灰度级差异的大体情况, 当局部均值差异较大时, 可以认为演化曲线轮廓靠近真实图像边缘, 能量向最小值逼近, 因此我们将其用来计算模型的能量项, 加速曲线的能量收敛; 而局部灰度方差差异则表示轮廓内外局部邻域间像素灰度值的方差差异, 反映了轮廓内外局部区域灰度的匀质性差异, 因此我们将其代替LBF模型中的参数λ1、λ2作为轮廓内外局部能量参数值的控制项。令LM1(x)和LM2(x)分别代表像素点x处的轮廓内外局部灰度均值, 其定义如下:
| $ L{M_1}\left( x \right) = \frac{{\int_\Omega {R\left( {x,y} \right)I\left( y \right){H_\varepsilon }\left( {\phi \left( y \right)} \right){\rm{d}}y} }}{{\int_\Omega {R\left( {x,y} \right){H_\varepsilon }\left( {\phi \left( y \right)} \right){\rm{d}}y} }} $ | (7) |
| $ L{M_2}\left( x \right) = \frac{{\int_\Omega {R\left( {x,y} \right)I\left( y \right)\left( {1 - {H_\varepsilon }\left( {\phi \left( y \right)} \right)} \right){\rm{d}}y} }}{{\int_\Omega {R\left( {x,y} \right)\left( {1 - {H_\varepsilon }\left( {\phi \left( y \right)} \right)} \right){\rm{d}}y} }} $ | (8) |
则其对应的局部均值差异和局部方差差异被定义为:
| $ {\varepsilon ^{_{LMD}}} = \gamma \int_\Omega {{{\left| {L{M_1}\left( x \right) - L{M_2}\left( x \right)} \right|}^2}{\rm{d}}x} $ | (9) |
| $ LS{D_1} = \int_\Omega {\frac{{{{\left| {st{d^2}\left( {L{M_1}\left( x \right)} \right) - st{d^2}\left( {L{M_2}\left( x \right)} \right)} \right|}^{\frac{1}{2}}}}}{{std\left( {L{M_2}\left( x \right)} \right)}}dx} $ | (10) |
| $ LS{D_2} = \int_\Omega {\frac{{{{\left| {st{d^2}\left( {L{M_1}\left( x \right)} \right) - st{d^2}\left( {L{M_2}\left( x \right)} \right)} \right|}^{\frac{1}{2}}}}}{{std\left( {L{M_1}\left( x \right)} \right)}}dx} $ | (11) |
其中, γ是负常数, std (Y)表示Y的标准差, εLMD为局部均值差异, LSD1和LSD2为局部方差差异。当曲线内部局部灰度方差大于外部时, 即std (LM1(X))> std (LM2(X)), 可以认为曲线内部匀质性低于外部匀质性, 此时, 应增加曲线内部能量所占权重, 来降低其对曲线演化的影响; 同理std (LM1(X)) < std (LM2(X))时, 增加曲线外部能量所占比重, 当两者相差较小时, 能量函数达到最优。综上所述, 本文模型的总能量泛函被定义为:
| $ \begin{array}{l} {E^{FALD}} = \mu \int_\Omega {\frac{1}{2}{{\left( {\left| {\nabla \phi \left( x \right)} \right| - 1} \right)}^2}dx} + \\ + v\int_\Omega {\left| {\nabla {H_\varepsilon }\left( {\phi \left( x \right)} \right)} \right|dx} + {\varepsilon ^{_{LMD}}}\\ + LS{D_1}\int_\Omega {FALD\left( {x,L{M_1}\left( x \right)} \right){H_\varepsilon }\left( {\phi \left( x \right)} \right){\rm{d}}x} \\ + LS{D_2}\int_\Omega {FALD\left( {x,L{M_2}\left( x \right)} \right)\left( {1 - {H_\varepsilon }\left( {\phi \left( x \right)} \right)} \right){\rm{d}}x} \\ = \mu \int_\Omega {\frac{1}{2}{{\left( {\left| {\nabla \phi \left( x \right)} \right| - 1} \right)}^2}dx} + v\int_\Omega {\left| {\nabla {H_\varepsilon }\left( {\phi \left( x \right)} \right)} \right|dx} + \gamma \\ \int_\Omega {{{\left| {L{M_1}\left( x \right) - L{M_2}\left( x \right)} \right|}^2}dx} \\ + LS{D_1}\int_\Omega {\left( {\int_{\left( {y \in {N_x}} \right) \ne x} {\frac{{{{\left| {I\left( y \right) - L{M_1}\left( x \right)} \right|}^2}}}{{D\left( {x,y} \right)}}dy} } \right){H_\varepsilon }\left( {\phi \left( x \right)} \right){\rm{d}}x} \\ + LS{D_2}\int_\Omega {\left( {\int_{\left( {y \in {N_x}} \right) \ne x} {\frac{{{{\left| {I\left( y \right) - L{M_2}\left( x \right)} \right|}^2}}}{{D\left( {x,y} \right)}}dy} } \right)} \\ \left( {1 - {H_\varepsilon }\left( {\phi \left( x \right)} \right)} \right){\rm{d}}x \end{array} $ | (12) |
采用梯度下降法, 最小化总能量泛函得到曲线演化方程及其对应的迭代方程如下:
| $ \begin{array}{l} \frac{{\partial \phi \left( x \right)}}{{\partial t}} = {\delta _\varepsilon }\left( {\phi \left( x \right)} \right)\left[ {LS{D_2}{e_2} - LS{D_1}{e_1} + {\varepsilon ^{LMD}}} \right]\\ + \mu \left( {{\nabla ^2}\phi - {\rm{div}}\left( {\frac{{\nabla \phi }}{{\left| {\nabla \phi } \right|}}} \right)} \right) + v\delta \left( \phi \right){\rm{div}}\left( {\frac{{\nabla \phi }}{{\left| {\nabla \phi } \right|}}} \right) \end{array} $ | (13) |
| $ {\phi ^{\left( {t + 1} \right)}} = {\phi ^{\left( t \right)}} + \frac{{\partial \phi }}{{\partial t}}\Delta t $ | (14) |
其中, εLMD、LSD1和LSD2分别由式(9)、(10)和(11)给出, δε为Dirac函数, 由式(3)给出。
| $ {e_1} = \int_{\left( {y \in {N_x}} \right) \ne x} {\frac{{{{\left| {I\left( y \right) - L{M_1}\left( x \right)} \right|}^2}}}{{D\left( {x,y} \right)}}dy} , $ |
| $ {e_2} = \int_{\left( {y \in {N_x}} \right) \ne x} {\frac{{{{\left| {I\left( y \right) - L{M_2}\left( x \right)} \right|}^2}}}{{D\left( {x,y} \right)}}dy} 。$ |
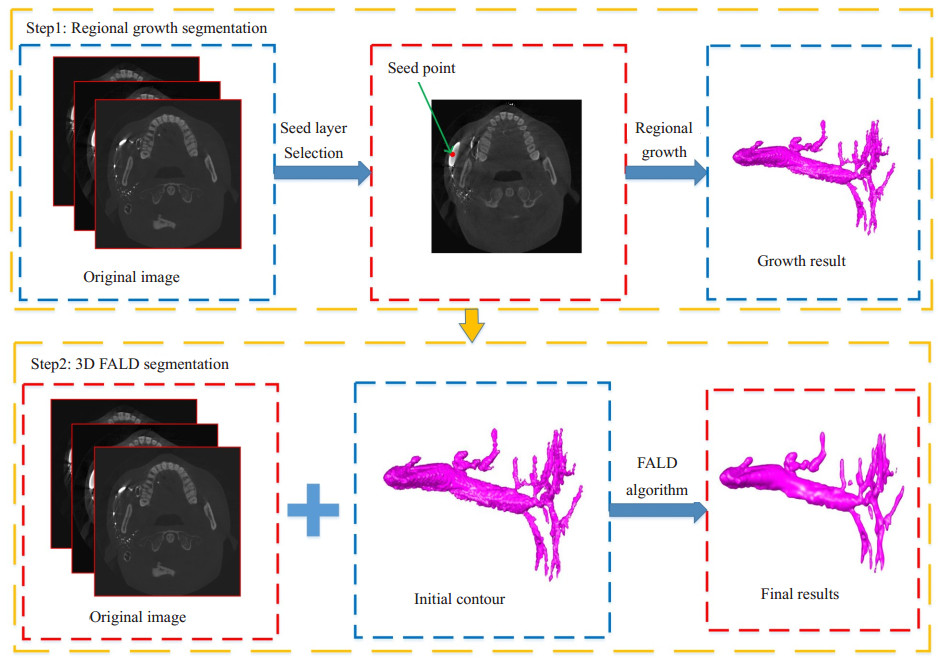
在RLSF模型中, 运用不可压缩的两相流算法来实现水平集的重新初始化, 保证了演化曲线的平滑特性[29], 本文算法应用LBF模型的方法, 无需重新初始化零水平集, 也能保证曲线演化过程中的平滑性。在分割3D腮腺图像时, 我们在传统的区域分割方法[30]基础上, 根据待分割图像的局部灰度差异以及其空间结构信息, 利用FALD算法对区域生长分割结果进行矫正。图 2为3D算法的流程图, 在step1中, 首先从原图中选出种子层及对应的种子点, 完成区域生长, 得到初步的分割结果, 然后在step2中, 将其作为三维FALD算法的初始轮廓, 最后得到准确的三维分割结果。
|
图 2 3D腮腺图像分割算法流程图 Fig.2 Flow chart of 3D parotid image segmentation algorithm. |
为验证本文算法在腮腺导管CT图像分割上的可行性及优越性, 我们对大量的腮腺图像进行了分割实验, 并且将本文模型FALD分别与C-V模型、LBF模型和RLSF模型的分割结果作对比。本文实验是在Intel (R) Core (TM)3.60 GHz CPU、8.0 GB RAM的PC机上, 使用Matlab R2014b软件实现的。实验中, 参数取值为γ=-1.0, ε=1.0, 步长Δt=0.1, 距离保持项系数μ=1.0, 圆形邻域半径r=7, 矩形邻域窗口大小为5×5。
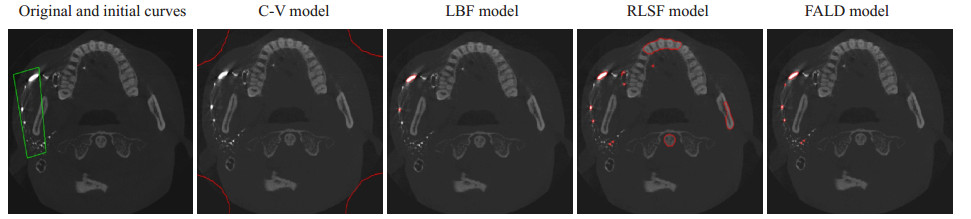
3.1 二维腮腺图像分割实验我们先对同一单侧腮腺图像分割结果进行对比, FALD模型、LBF模型以及其它模型的各参数设置为ν=0.5 × 255 × 255, λ1=λ2=1.0, σ=3.0, Iter=1000。图 3所示, 绿色曲线代表初始轮廓线, 红线代表最终演化曲线, (A)为待分割的原始图像, 图像中含有较多的模糊边界, 并且还存在其它弱梯度边界的影响。(B)是C-V模型分割结果, 可明显看出演化曲线最终停留在两均匀灰度区域之间的边界上, 未对图像进行进一步细致的目标区域分割。(C)是LBF模型的分割结果, 最终演化曲线仅停留在部分目标区域, 对于一些边界模糊的目标, 并没有从原图中分割出来。(D)为RLSF模型的分割结果, 该模型将大部分目标区域都进行了较准确地分割, 并且保留了边界细节, 但其对非目标区域也进行了分割。(E)是本文FALD模型的分割结果, 可观察到即使对于细小的颗粒目标, 最终的演化曲线也能够准确地停留在其边界上。
|
图 3 单侧腮腺导管分割结果对比 Fig.3 Comparison of the results of unilateral parotid duct segmentation. |
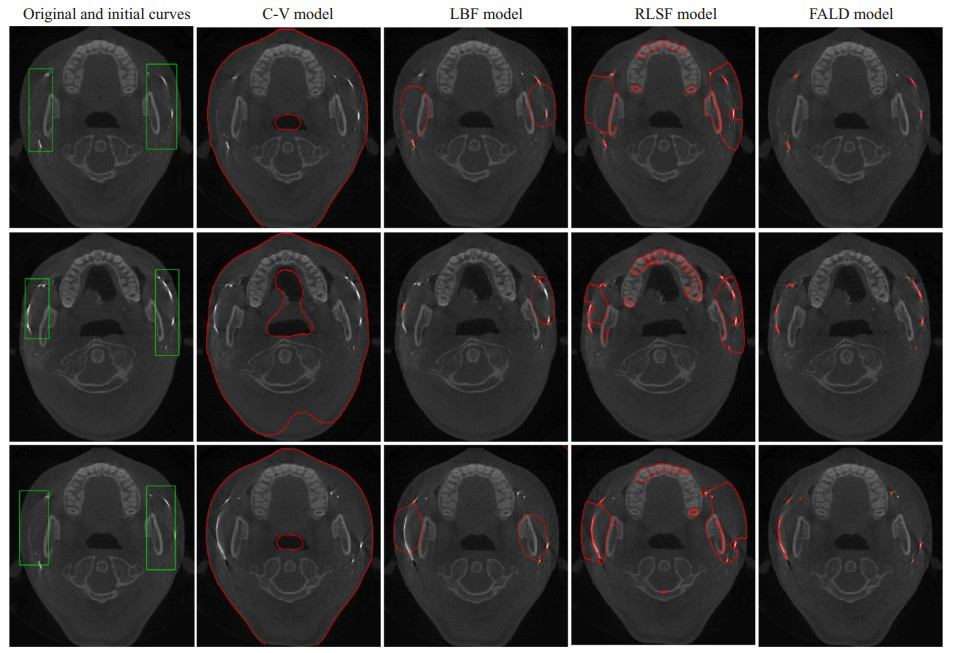
我们还对一系列的双侧腮腺图像进行了实验, 实验参数:ν=0.2 × 255 × 255, Iter=2000, 其它参数设置与分割单边腮腺图像时相同。图 4(A)为3幅不同的双边腮腺图像和初始曲线, (B)~(E)依次对应为C-V模型、LBF模型、RLSF模型和本文模型的分割结果。从图中不难看出C-V模型、LBF模型图像细节不如FALD模型, 而RLSF模型在弱边缘处理上也和FALD模型相差很大。
|
图 4 双侧腮腺导管分割结果对比 Fig.4 Comparison of the results of bilateral parotid duct segmentation. |
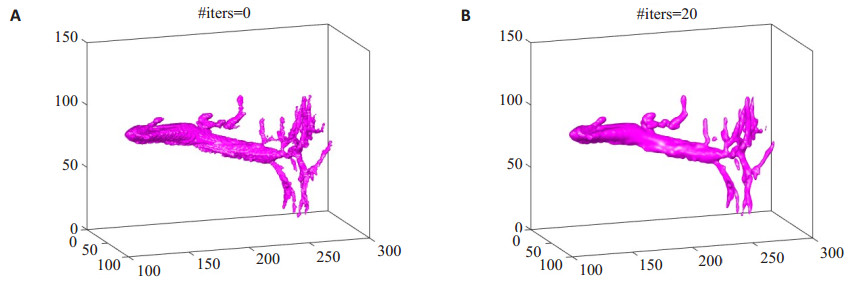
为更直观地展现本文算法腮腺的分割结果, 我们进行了三维腮腺图像的分割实验, 实验参数:v=0.01, Iter=20, 其它参数设置与分割二维腮腺图像相同。图 5为算法分割后的三维重建结果, (A)图为区域生长后的结果, 将其作为FALD算法的初始轮廓进行演化, 迭代20次得到最终的分割结果如(B)图所示。从图中不难看出, 区域生长的结果含有阶梯状灰度, 表面多毛刺、凹凸不均匀, 而经过FALD算法之后表面变得平滑、连续, 这是由于在分割过程中引入了原图边界的局部灰度差异信息, 对复杂梯度边界上错误分割点进行矫正, 从而得到了正确的分割结果。
|
图 5 三维腮腺导管分割重建结果 Fig.5 Results of three-dimensional reconstruction of the parotid duct. A: The initial contour; B: 3D FALD segmentation results |
从上述实验结果可以看出, C-V模型对腮腺图像中局部区域未进行准确分割, 这是由于该模型在分割过程中仅考虑了全局区域的灰度信息, 并未注意局部细节; 而LBF模型和RLSF模型虽然考虑了局部邻域的灰度信息, 但受弱梯度边缘的影响, 最终都未对腮腺图像中的目标区域实现精确地分割; 本文模型由于引入了局部邻域的灰度差异, 较好地表达了目标区域的局部信息, 并且利用局部相似因子来克服不均匀灰度和噪声的影响, 因而对腮腺图像实现了准确地分割。
目前, 活动轮廓模型已广泛应用于各个领域, 特别是应用于医学[31-32]和人工智能领域。本文讨论了传统活动轮廓模型在腮腺导管图像上分割的局限性, 并针对腮腺导管图像灰度不均匀、噪声以及边界模糊等缺点提出了一种新的基于局部灰度差异的快速自适应分割算法。利用局部方差差异调节曲线轮廓内外部能量所占比重, 使曲线在演化过程中能够自适应地准确收敛至目标区域边界, 克服了以往模型对参数敏感这一难题, 并且本文模型首次引入局部均值差异作为能量项以及方差差异作为控制项, 使曲线演化被长度项约束的同时, 可以自适应地调整曲线进化速度和方向, 加快了曲线收敛, 因此在较少的迭代次数中就可以得到较好的分割结果。我们在大量的临床数据上进行了实验, 分割结果表明, 本文算法的性能远高于传统的算法。
本文模型仍然存在一些局限性, 首先, 类似于大多数传统的模型, FALD模型未解决对初始轮廓敏感这一问题, 不同初始轮廓可能对最终的分割影响很大; 其次, 本文算法虽能分割出大多数腮腺导管, 但在一些极细导管的分割上仍存在缺陷, 值得注意的是, 虽然该算法目前只应用于对腮腺图像的分割, 但它仍然有望可以应用于其它领域的图像分割, 后续将对这些问题进行实验研究。
| [1] |
Horsburgh A, Massoud T. The role of salivary duct morphology in the aetiology of sialadenitis:statistical analysis of sialographic features[J].
Int J Oral Maxillofac Surg, 2013, 42(1): 124-8.
DOI: 10.1016/j.ijom.2012.10.006. |
| [2] |
Drage NA, Wilson RF, Mcgurk M. The genu of the submandibular duct-Is the angle significant in salivary gland disease?[J].
Dentomaxillofac Radiol, 2002, 31(1): 15-8.
DOI: 10.1038/sj.dmfr.4600653. |
| [3] |
Horsburgh A, Massoud TF. The salivary ducts of Wharton and Stenson:Analysis of normal variant sialographic morphometry and a historical review[J].
Ann Anat, 2013, 195(3): 238-42.
DOI: 10.1016/j.aanat.2012.11.003. |
| [4] |
Zenk J, Hosemann WG, Iro H. 1998.Diameters of the main excretory ducts of the adult human submandibular and parotid gland:a histologic study[J].
Oral Surgery Oral Medicine Oral Pathology Oral, 1998, 85(5): 576-80.
DOI: 10.1016/S1079-2104(98)90294-3. |
| [5] |
Hou ZQ, Han CZ. Force field analysis snake:an improved parametric active contour model[J].
Pattern Recognit Lett, 2005, 26(5): 513-26.
DOI: 10.1016/j.patrec.2004.09.001. |
| [6] |
Al-Diri B, Hunter A, Steel D. Snakes:an active contour model for segmenting and measuring retinal vessels[J].
IEEE Trans Med Imaging, 2009, 28(9): 1488-97.
DOI: 10.1109/TMI.2009.2017941. |
| [7] |
Srikrishnan V, Chaudhuri S. Adaptive smoothness based robust active contours[J].
Image Vis Comput, 2011, 29(5): 317-28.
DOI: 10.1016/j.imavis.2010.12.004. |
| [8] |
Zhu SC, Yuille A. Region competition:Unifying snakes, region growing, and Bayes/MDL for multiband image segmentation[J].
IEEE Transactions on Pattern Analysis&Machine Intelligence, 1996, 18(9): 884-900.
|
| [9] |
Song TH, Sanchez V, Eldaly H. Dual-Channel active contour model for megakaryocytic cell segmentation in bone marrow trephine histology images[J].
IEEE Trans Biomed Eng, 2017, 64(12): 2913-23.
DOI: 10.1109/TBME.2017.2690863. |
| [10] |
Horvath P, Jermyn I, Zerubia J, et al.A Higher-Order active contour model for tree detection[C].Hongkong, China: IEEE, 2006.
|
| [11] |
Wang JX, Zhao SF, Liu ZF.Segmentation of cerebral vascular structures using an active contour model[C].Hangzhou, China: IEEE, 2016, 6(2): 31-5.
|
| [12] |
Kass M, Witkin A, Terzopoulos D. Snakes:active contour models[J].
Int J Comput Vis, 1988, 1(4): 321-31.
DOI: 10.1007/BF00133570. |
| [13] |
Caselles V, Coll T. A geometric model for active contours in image processing[J].
Numerische Mathematik, 1993, 66(1): 1-31.
DOI: 10.1007/BF01385685. |
| [14] |
Malladi R, Sethian JA, Vemuri BC. Shape modeling with front propagation:a level set approach[J].
IEEE Trans Pami, 1995, 17(2): 158-75.
DOI: 10.1109/34.368173. |
| [15] |
Caselles V, Kimmel R, Sapiro G. Geodesic active contours[J].
Int J Comput Vis, 1997, 22(1): 61-79.
DOI: 10.1023/A:1007979827043. |
| [16] |
Vasilevskiy A, Siddiqi K. Flux maximizing geometric flows[J].
IEEE International Conference on Computer Vision, 2002, 24(12): 149-54.
|
| [17] |
Chan TF, Vese LA.Image segmentation based on active contour without edges[C].Cluj-Napoca, Romania: IEEE, 2012.
|
| [18] |
Tsai A, Yezzi A, Willsky AS.Curve evolution implementation of the Mumford-Shah functional for image segmentation, denoising, interpolation, and magnification[C].IEEE T Image Process, 2001, 10(8): 1169-86.
|
| [19] |
Vese LA, Chan TF. A multiphase level set framework for image segmentation using the Mumford and Shah model[J].
Int J Comput Vis, 2002, 50(3): 271-93.
DOI: 10.1023/A:1020874308076. |
| [20] |
Ronfard R. Region-based strategies for active contour models[J].
Int J Comput Vis, 1994, 13(2): 229-51.
DOI: 10.1007/BF01427153. |
| [21] |
Estellers V, Zosso D, Lai R, et al. Efficient algorithm for level set method preserving distance function[J].
IEEE Trans Image Process, 2012, 21(12): 4722-34.
DOI: 10.1109/TIP.2012.2202674. |
| [22] |
Mumford D, Shah J. Optimal approximations by piecewise smooth functions and associated variational-problems[J].
Commun Pur Appl Math, 1989, 42(5): 577-685.
DOI: 10.1002/(ISSN)1097-0312. |
| [23] |
Lie J, Lysaker M, Tai XC. A binary level set model and some applications to Mumford-Shah image segmentation[J].
IEEE T Image Process, 2006, 15(5): 1171-81.
DOI: 10.1109/TIP.2005.863956. |
| [24] |
Li CM, Xu CY, Gui CF.Level set evolution without ReInitialization: A new variational formulation[C].Sam Diego, Ca, USA: IEEE, 2005.
|
| [25] |
Li C, Huang R, Ding Z, et al. A level set method for image segmentation in the presence of intensity inhomogeneities with application to MRI[J].
IEEE Trans Image Process, 2011, 20(7): 2007-16.
DOI: 10.1109/TIP.2011.2146190. |
| [26] |
Li CM, Gore J, Ding ZH. Implicit active contours driven by local binary fitting energy[J].
Pattern Recogn, 2010, 43(4): 1199-1206.
DOI: 10.1016/j.patcog.2009.10.010. |
| [27] |
Niu SJ, Chen Q, Ji ZX, et al. Robust noise region-based active contour model via local similarity factor for image segmentation[J].
Pattern Recognit, 2017, 61(1): 104-19.
|
| [28] |
Han X, Xu CY, Prince JL. A topology preserving level set method for geometric deformable models[J].
IEEE Trans Pattern Anal Mach Intell, 2003, 25(6): 755-68.
DOI: 10.1109/TPAMI.2003.1201824. |
| [29] |
Sussman M, Smereka P, Osher S. A level set approach for computing solutions to incompressible two-phase flow[J].
J Comput Phys, 1994, 114(1): 146-59.
DOI: 10.1006/jcph.1994.1155. |
| [30] |
Adams R, Bischof L. Seeded region growing[J].
IEEE Trans Pattern Anal Mach Intell, 1994, 16(6): 641-7.
DOI: 10.1109/34.295913. |
| [31] |
Lee ME, Park SY, Cho WH, et al.Medical image segmentation using a geometric active contour model based on level set method [C].Victoria, BC.Canada: IEEE, 2007.
|
| [32] |
Ebrahimdoost Y, Dehmeshki J, Ellis TS, et al.Medical image segmentation using active contours and a level set model: application to pulmonary embolism (PE) segmentation[C].St Moarten Netherlands: IEEE, 2010.
|
 2018, Vol. 38
2018, Vol. 38

