肿瘤放射治疗计划的优化设计是实现放疗基本目标的关键临床步骤，其本质是一个多目标优化问题^[1]，目标单元为各感兴趣区域的剂量学表现。考虑到实际靶区高剂量覆盖率的达成与周边危机器官和正常组织器官受量的减少间存在固有矛盾^[2-4]，临床往往只能通过计划设计人员依据个人经验以人工试错方式多次调整目标达成情况，以期获取各目标单元间的最佳权衡。这种依靠人工调整的计划优化方法制约了计划设计过程的自动化实现，同时也是造成当前临床放疗计划高水平同质化程度不高的重要原因^[5-8]。对此，不少学者就模拟计划人员实际调整并权衡各目标单元的剂量学表现的思维，提出了将临床喜好量化为初始约束优先级列表并不断自动调整的多目标优化方法^[9-12]，然而方法中存在逐项考虑而非多项同步调整、引入非剂量学考量项等低效行为，抑或需要求解大规模的非线性优化问题，求解难度大且时间耗费较长等。此外，优化过程中选用的优化模型也多为基于器官惩罚的方法，限制了优化解空间Pareto平面的搜索范围，难以保证所得最优解^[13]。部分研究表明^[14-15]，将器官中的体素的调整权限进行释放，调整为基于体素惩罚的方法，可有效将解空间由Pareto平面子集扩展为全集，保障最优解的获取。该方法中如何根据预设条件自动调整体素权重是重点。针对以上两点，本文优化方法对其分别进行了改进并作了有力地结合，提出了一种仅考虑剂量学表现、但可同时对具有同等优先权的多个指征项进行批次调整的自动多目标优化方法，在此基础上，将上述基于器官惩罚模型转化为基于体素惩罚优化模型的约束，形成可自动高效调整计划剂量约束并尽可能生成该条件下全局最优解的整体解决方案，实现调强放疗(IMRT)的自动多目标优化。

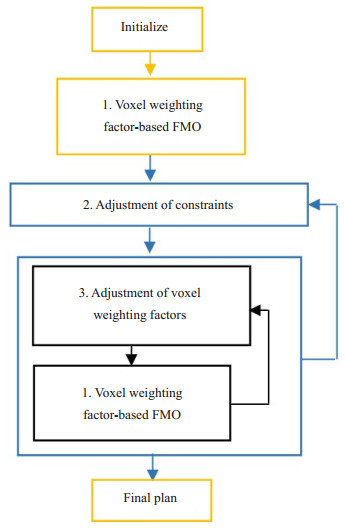
基于约束优先级列表的IMRT自动多目标优化方法首先在初始剂量约束条件下调用基于体素权重因子的FMO优化生成初始剂量分布，然后以约束优先级列表为依据，分步对剂量约束进行调整，使各约束随迭代进行时逐步达到最佳设置状态。剂量约束每调整1次，紧随调用基于体素权重因子的FMO模型，解得满足当前约束的全局最优计划。基于约束优先级列表的IMRT多目标优化具体实现流程如图 1所示。

图 1(Figure 1)

图 1 基于约束优先级列表的IMRT自动多目标优化流程图 Figure 1 Constraint priority list-dependent IMRT automatic multi-objective optimization framework.

为了保障计划结果符合临床要求，剂量约束首先被分成硬约束和软约束。硬约束指不能违反的剂量约束，不会被松弛或拉紧；软约束指在优化中可被松弛或收紧的剂量约束，随着优化的进行可升级成硬约束。靶区高剂量照射和保护OAR是计划设计的目的，也是判断计划是否符合临床要求的重要依据，结合宫颈癌IMRT计划的相关规范(International evaluation of radiotherapy technology effectiveness in cervical cancer)和临床计划设计经验，本文采用取整的方式将PTV的D_99%、D_97%、V₄₉紧化并将D_99%、D_97%、V₄₉、D_max和Body的D_max设为硬约束。此外，为了保障剂量分布的适形度，引入感兴趣区域“Body-(PTV+1)”，即Body减去(PTV外扩1厘米)，将其最大剂量约束也设为硬约束。宫颈癌IMRT计划的相关规范涉及的直肠、膀胱、肠、股骨头和骨骼所对应的剂量约束设为软约束，其中结合临床计划设计经验将直肠的V₃₀初始值设为100%。最后根据临床对软约束的重视程度由临床医生进行分类和排序，将相似重视程度的软约束被分成相同或相邻的等级，形成宫颈癌病例的约束优先级列表如表 1所示，第4列不同的数字表示不同优先级的剂量约束，数字“0”对应的剂量约束优先级最高，随着数字增加，优先级逐渐减低。

表 1(Table 1)

表 1 处方剂量为4500 cGy的宫颈癌病例的初始约束优先级列表 Table 1 Initial constraint priority list of cervical cancer patients with a prescribed dose of 4500 cGy ROI Endpoint Initial value Priority PTV D99% 41 Gy 0 PTV D97% 44 Gy 0 PTV V49 10% 0 PTV Dmax 50 Gy 0 Body Dmax 50 Gy 0 Body-(PTV+1) Dmax 43 Gy 0 Rectum V45 50% 1 Bladder V45 50% 1 Rectum V30 100% 2 Bowel V40 30% 2 Femoral heads V30 15% 2 Bone V20 66% 3 Bone V10 80% 3

表 1 处方剂量为4500 cGy的宫颈癌病例的初始约束优先级列表 Table 1 Initial constraint priority list of cervical cancer patients with a prescribed dose of 4500 cGy

在初始化器官权重因子、体素权重因子、理想剂量分布和初始剂量约束条件后，基于约束优先级列表的IMRT多目标优化方法进行最大迭代次数为N1的FMO优化得到初始剂量分布。然后参考Breedveld等人提出的剂量约束调整方法，本文分3步实现剂量约束的调整。

第1步：若初始剂量分布不满足初始剂量约束条件，进入第1步松弛剂量约束，否则跳到第3步。第1步按优先级低高的顺序松弛违反的剂量约束中处于最低优先级的所有剂量约束后，在当前剂量约束条件下进行最大迭代次数为N2的FMO优化，多次重复操作，直到得到满足当前剂量约束条件的计划为止。松弛方法是在当前计划结果下将剂量约束值增加0.5%，例如计划结果中该剂量约束值为32.81%，则松弛后的剂量约束值为33.31%。

第2步：按优先级高低的顺序一个一个地拉紧第一步计划结果中不满足初始剂量约束条件的剂量约束。每次拉紧剂量约束后，进行最大迭代次数为N3的FMO优化，直到满足当前剂量约束条件(该剂量约束值满足初始剂量约束要求)或达到最大迭代次数N3后将该剂量约束升级为硬约束，否则继续拉紧该剂量约束。

第3步：按照优先级高低的顺序，依次一个一个拉紧剂量约束。每次剂量约束拉紧后，进行FMO优化，直到达到最大迭代次数N4将该剂量约束升级为硬约束，否则继续拉紧该剂量约束。当全部软约束升级成硬约束，优化停止，此时得到最终的计划。拉紧剂量约束的方式是在当前计划结果下将当前剂量约束值减少0.5%。

本文采用的基于体素权重因子的FMO模型的目标函数如式(1)所示^[16-17]，

第1项衡量了计算剂量值和理想剂量值之间的差别，其中x为射野强度分布向量。D_v为剂量沉积矩阵，d_v^p为理想的剂量分布(PTV是处方剂量4500cGy，其余OARs为0)。ξ_v为器官权重因子，ῆ_v为体素权重因子。第2项是光滑项，其中s为光滑因子，M是一个算子，等于Δx除以x，Δx为射野强度分布向量x的拉普拉斯离散化。C为一个常数，g_i(x)≤0为剂量约束，m为剂量约束数目。优化算法为BOXCQP^[18]，剂量计算为CERR^[19]中IMRTP部分的QIB剂量计算引擎。

内循环对体素权重因子的调整包含两个过程：调整体素的选择和体素权重值的更新。本文涉及到的剂量约束有临床上常用的剂量约束和剂量-体积约束。若PTV或某一OAR存在最大剂量约束D_max ≤ D_c，其中D_c为临界剂量值，则调整剂量值大于D_c部分体素的权重值。

对于剂量-体积约束，调整剂量值接近临界剂量的体素的权重值比调整剂量值远离临界剂量的体素的权重值更加有效^[20]。若PTV和某一OAR存在最小剂量-体积约束V_Dc ≤ V_c，即大于剂量值D_c的体积要小于等于V_c，则调整剂量值处于区间[D_c, D](为临界体积V_c对应的剂量值，D > D_c)；若PTV存在最大剂量-体积约束D_Vc ≥ D_c，即大于剂量值D_c的体积要大于等于V_c，则调整剂量值处于[D, D_c], (D < D_c)部分体素的权重值。

体素权重值的更新策略如下：FMO模型首先将所有体素的权重因子初始化为1。对最小剂量约束和最大剂量-体积约束，体素权重因子的更新策略为$ w_i^{\left( {k + 1} \right)} = w_i^{\left( k \right)}{\left[ {\left( {{D_c} + \alpha } \right)/D_i^{\left( k \right)}} \right]^\mu }, \left( {D_i^{\left( k \right)} \le {D_c}} \right) $；对最大剂量约束和最小剂量-体积约束，体素权重因子的更新策略为$ w_i^{\left( {k + 1} \right)} = w_i^{\left( k \right)}{\left[ {\left( {D_i^{\left( k \right)} + \alpha } \right)/{D_c}} \right]^\mu }, \left( {D_i^{\left( k \right)} \le {D_c}} \right) $。其中w_i^(k)和w_i^(k+1)分别是第k和第(k+1)次迭代体素i的权重因子，第k次迭代体素i的剂量值为D_i^(k)。α > 0, μ > 1是由用户定义的，与优化速度、计划质量相关。

为了评估基于约束优先级列表的IMRT多目标优化方法对计划质量的改进效果，本文比较了6例宫颈癌病例的优化计划与原始(临床)计划的DVH和剂量约束点具体数值，并将剂量约束点结果进行配对T检验，研究剂量约束点结果在统计学上是否存在显著差异。

实验在基于Window 7操作系统下的Matlab2014a计算平台上进行，所用计算机为Intel 3.4 GHz 4核CPU。用于验证的6例宫颈癌病例采用6MV的光子束，进行7野(150⁰、100⁰，50⁰、0⁰、310⁰、260⁰、210⁰)共面照射。计划涉及的感兴趣区域有PTV、直肠、膀胱、肠、股骨头、骨骼、Body-(PTV+1)和Body，器官权重因子根据计划设计经验相应设成100、1、2、0.1、0.1、0.1、0.1和0.01，光滑因子s设为0.01，理想的剂量分布设PTV为处方剂量4500 cGy，其余感兴趣区域为0，所有体素权重因子的初始值为1。参数α, μ分别设为20和0.6，FMO模型的最大迭代次数N1、N2、N3、N4分别是30、1、30、30。其中参数α、μ和30是根据一系列的实验得到的经验参数。本文运用控制变量法研究不同的α, μ组合，目标函数值的收敛情况。实验结果表明，当α=0.6时，目标函数收敛到最小值所需的迭代次数随着μ增大而减少，且μ=20与μ=25几乎没变；当μ=20时，目标函数收敛到最小值所需的迭代次数随着α增大而减少，且α=0.6与α=1几乎没变。由于随着α, μ的增大，优化求解空间减小，因此本文将α, μ分别设为20和0.6。为了验证FMO模型目标函数的收敛性，对3个宫颈癌病例的目标函数值随着迭代次数的变化进行研究。实验结果显示，当迭代次数为30时，目标函数值就基本收敛到最小值。

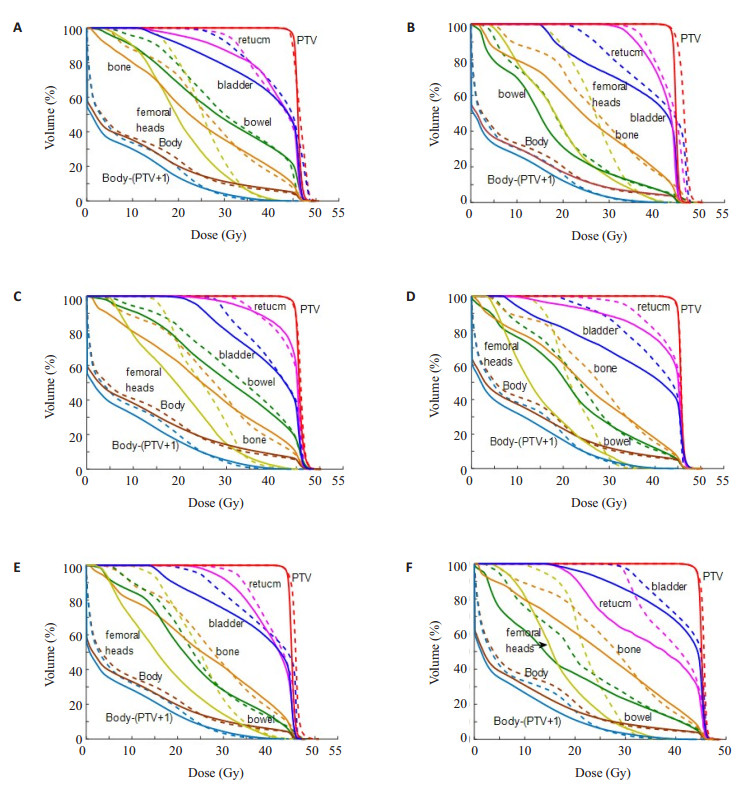
图 2是6例宫颈癌病例的DVH比较结果，其中实线为优化计划结果，虚线为原始(临床)计划结果。从DVH的比较结果可看出，优化计划在提高靶区覆盖率和均匀性的前提下，让周围正常组织、危及器官受到更低剂量的照射，更好地保护周围正常组织和危及器官。

图 2(Figure 2)

图 2 6例宫颈癌病例的DVH比较图 Figure 2 DVH comparison in the 6 cases of cervical cancer. Solid line: Optimized plan; Dashed line: Original plan.

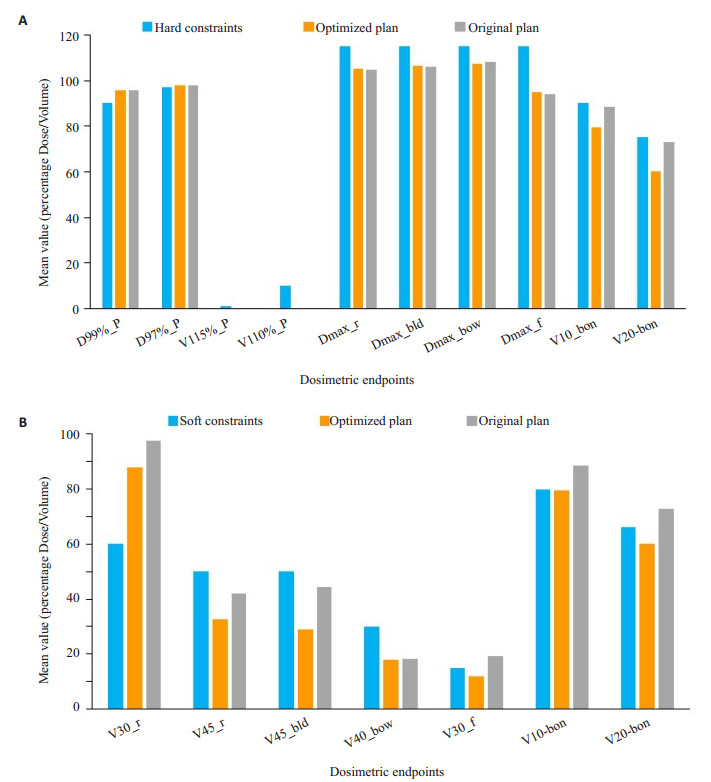
图 3将6例宫颈癌病例优化计划和原始(临床)计划在剂量约束点具体数值的平均结果进行比较，硬约束比较结果如图 3(A)所示，软约束的比较结果如图 3(B)所示。与原始(临床)计划相比，在PTV的D_99%、V_115%相同和满足OAR的硬约束的情况下，优化计划PTV的D_97%从43.97 Gy±0.27 Gy增到44.07 Gy±0.52 Gy，V_110%从(0.13±0.16)%减到(0.01 ± 0.01)%且V_115%不变；直肠的平均V₄₅从(41.99±13.31)%降到(32.55±22.27)%，平均V₃₀从(97.61±2.19)%降到(87.74±13.26)%；膀胱的平均V₄₅从(44.37±4.08)%降到(28.99±15.25)%；肠的平均V₄₀从(18.14±12.02)%降到(17.87±10.63)%；股骨头的平均V₃₀从(19.16±10.14)%降到(12.05±3.91)%；骨骼的平均V₂₀从(72.96±1.32)%降到(60.15±2.12)%，平均V₁₀从(88.55±0.74)%降到(79.60±0.29)%。以上结果表明，优化计划使得靶区的覆盖率和均匀性有所提升的同时，所有软约束的剂量约束点的数值下降。

图 3(Figure 3)

图 3 6例宫颈癌病例的剂量约束点平均结果比较 Figure 3 Comparison of endpoints in the 6 cases of cervical cancer. A: Hard constraints; B: Soft constraints.

为了从统计学的角度说明基于约束优先级列表的IMRT自动多目标优化方法可有效改进计划质量，本文将优化计划和原始(临床)计划在剂量约束点的具体数值两两配对进行配对的T检验，结果如表 2所示。在所有的13个剂量约束点当中，有3个是具有显著性差异的(P < 0.05)，分别是V_{30_f}、V_{10_bon}和V_{20_bon}。注意到PTV的D_99%和V_115%不在表 2中，是因为PTV的D_99%作为归一点且两组数据中PTV的V_115%都为0。

表 2(Table 2)

表 2 剂量约束配对t检验结果 Table 2 Paired t-test of the endpoint ROI Endpoint P ROI Endpoint P PTV D97% 0.4278 Bowel Dmax 0.7542 PTV V110% 0.1227 Bowel V40 0.7147 Rectum Dmax 0.6464 Femoral heads Dmax 0.6749 Rectum V45 0.1748 Femoral heads V30 0.0457 Rectum V30 0.0843 Bone V10 1.04E-06 Bladder Dmax 0.7374 Bone V20 3.01E-05 Bladder V45 0.059 - - -

表 2 剂量约束配对t检验结果 Table 2 Paired t-test of the endpoint

我们提出一种新的基于约束优先级列表的IMRT自动多目标优化方法，该方法按临床重视程度生成的约束优先级列表为依据，对剂量约束进行调整。该方法首先初始化器官权重因子、体素权重因子、理想剂量分布等输入，得到初始剂量分布。第1步判断初始剂量分布是否满足初始剂量约束条件，若计划结果满足初始剂量约束条件，则转向第3步。若计划结果不满足初始剂量约束条件，松弛违反剂量约束中处于最低优先级的所有剂量约束。第2步按优先级高低的顺序拉紧第一步结果中违反初始剂量约束条件的剂量约束，第3步拉紧的是其余的剂量约束，直到得到再次拉紧任意一个约束项都将会有其他剂量约束违反的计划。在每次调整剂量约束后，该方法调用基于体素权重因子的FMO模型反复优化计划，直到获得满足当前剂量约束条件的解或达到最大迭代次数后跳出，返回继续对剂量约束进行调整。为了验证优化方法的可行性，以6例子宫颈癌病例进行验证。

DVH比较结果显示，优化计划PTV的DVH曲线更加陡峭，OAR的DVH曲线大部分都在原始计划下方，说明优化计划PTV覆盖率和剂量均匀性提升，同时OAR接受剂量下降，更好实现放疗计划优化的目的。剂量约束点的平均对比结果从客观数据的角度说明了，在PTV覆盖率和剂量均匀性提升并且满足所有硬约束的同时，OAR剂量约束点具体数值下降，计划质量提升，这与DVH比较得到的结论是一致的；配对P检验比较结果中，骨骼的平均V₁₀和V₂₀均低于原始计划，且具有统计学差异(P < 0.05)，说明骨骼受照剂量降低是明显的；虽然直肠、膀胱、股骨头平均最大剂量D_max高于原始计划，但是其满足硬约束，且两者之间不具有统计学差异(P > 0.05)，说明直肠、膀胱、股骨头最大剂量的增加是不明显的，所以其增加是可以接受的。其余剂量约束项不具有统计学差异(P > 0.05)，说明PTV覆盖率、剂量均匀性和其剂量约束的质量是相当的。此外，DVH比较结果中，优化计划少数OAR的DVH曲线与原始计划之间存在交叉，但交叉出现的区域极少存在临床规范关注的剂量约束点，可能是由于对规范中的剂量约束点更多关注。

基于约束优先级列表的IMRT自动多目标优化方法实现方式是先生成约束优先级列表，根据该表对剂量约束松弛或拉紧，整个优化过程中不需要在添加额外的人工干预，减少计划设计者的工作量，提高计划设计效率。对于计划的多目标优化问题，另一种比较成熟的方法是Pareto平面检索方法^[21-24]。Pareto平面检索方法在生成一系列计划后，需要检索当中最优的计划，这是当前一个难题。而基于约束优先级列表的IMRT多目标优化不需要计划设计者手动或者自动地的挑选计划，在实现自动的多目标优化方面具有天然的优势。

此外，基于体素权重因子的FMO模型优化比临床上采用的基于器官权重因子的优化方法扩展求解空间，可得到质量更优的计划。然而，由于体素权重因子与DVH曲线的关系是未知的，还不能从数学上证明方法中采用的基于体素权重因子的调整方法的收敛性。另一方面，本方法采用的基于约束优先级列表的多目标优化方法是比较费时的，接下来需要对其进行GPU加速^[25-27]或者运用其他方法减少计划优化花费的时间。