2. 中山大学肿瘤防治中心,广东 广州 510060
2. Sun Yat-sen University Cancer Center, Guangzhou 510060, China
肿瘤放射治疗是肿瘤治疗的三大手段之一,其基本目标是实现治疗增益比的最大化, 计划设计则是实现该目标的关键步骤[1-2]。当前临床计划设计过程常采用人工试错方法[3],且质量审核多看其计划剂量学表现,而该表现标准又以基于患者群体统计所得的相关临床规范为参照,缺乏患者个体结构差异性的考虑,最终导致患者所接受的临床放疗计划同质化程度不高,制约了放疗基本目标的实现[4-6]。临床经验及研究表明[7-8],不同患者可达质优计划的剂量学特性与其几何解剖结构特性具有较强的相关性,通过对该相关性进行学习与建模[9],从而使得新患者在对其进行计划设计前便可准确地预测出对应质优计划的剂量学目标。将该目标作为实际临床计划设计的质量审核标准,便可为个体化计划设计质量控制提供精准的度量,有效提高临床放疗计划的高水平同质化程度[10-11]。目前已有研究主要集中在初步关联模型的建立以及主要影响因素的探究上[12-15],虽然在部分病例中能得到较好的结果,但依旧存在模型较为主观与粗糙、患者个体特性的提取不完善等缺陷;此外,计划剂量学特性的提取也多以简单的一维剂量体积指征项或二维DVH曲线为主,未能体现剂量点的位置信息,对于部分肿瘤类型而言,并不足以充分提供临床医生所需查看的剂量信息。
本研究创新性提出了,一种基于神经网络[16]的患者几何解剖结构和器官三维剂量分布的关联模型,不仅充分考虑了射线角度、器官体积和器官间空间位置关系等影响因素,且使得计划剂量学特征表达为携带位置信息且细化、丰富化程度更高的三维剂量分布,有效保留所有体素的剂量信息和空间位置关系,为后续计划优化和计划质量控制提供更为充分的数据信息。
1 材料和方法 1.1 实验数据本研究回顾性采集了25例临床前列腺癌IMRT/SBRT计划数据,数据包含CT图像、治疗计划和计划剂量分布。放疗计划放置13个照射野,每个照射野角度固定,处方剂量为50 Gy,且计划包含由临床医生勾画的计划靶区(PTV)与危及器官(OAR)轮廓线、划分体素尺寸、等中心点坐标等信息。放疗计划与剂量分布数据由Pinnacle放疗计划系统(TPS)优化生成,导出放疗计划为DICOM格式数据。
1.2 方法概述与模型框架本文研究思路为,收集临床放疗计划数据,提取与剂量分布相关特征信息,并将数据随机划分为训练集与验证集,利用神经网络学习方法构建剂量预测模型,训练集用于模型训练,验证集用于检验模型预测能力。收集的25例临床前列腺癌IMRT/SBRT计划数据,通过对比临床计划TPS剂量分布与预测模型输出剂量分布,用于验证本文提出模型的有效性与稳定性。
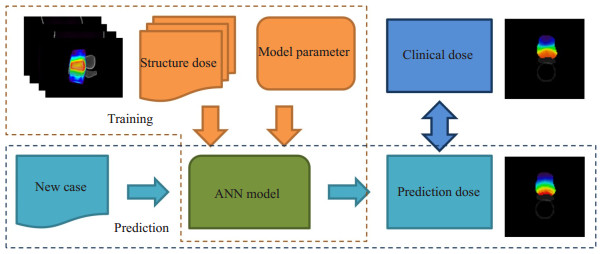
三维剂量分布预测模型构建框架如图 1所示,模型建立分为训练和预测(验证)两个阶段。首先需要收集临床放疗计划,通过人工筛选同类型计划并从临床数据中提取本研究所需的信息。再者,将病例数据随机划分训练与预测(验证)两组,通过多次训练与验证确定模型稳定性。最后预测验证集剂量,通过剂量差异对比分析,验证模型有效性。
|
图 1 模型训练与预测流程框架 Figure 1 Framework for model training and prediction. |
计划数据包括剂量分布信息和感兴趣区域(ROIs)的轮廓线信息,其中ROIs包括靶区和危及器官,如前列腺、膀胱、直肠和股骨头等。临床数据收集后需首先对其进行数据处理,处理方法为使用MATLAB对其进行基础数据读取和转化。本文选取的OAR器官为膀胱、直肠和股骨头,分别对其建立剂量预测模型。根据以往研究结果[7, 13-15]提取9个几何特性特征,空间位置上,提取的是体素对象到PTV边界的最近距离、到其余OAR边界的距离、到照射等中心的距离以及相对于其的球坐标角度等;器官体积上,提取了PTV的体积。
综上,本文选取的9个代表患者几何特异性的输入特征为:
1. rPTV:体素到PTV边界的距离
2. rBladder:体素到膀胱边界的距离
3. rRectum:体素到直肠边界的距离
4. rFemur_R:体素到右股骨头边界的距离
5. rFemur_L:体素到左股骨头边界的距离
6. risocenter:体素到等中心点的距离
7. VPTV:PTV的体积
8. Θ:球坐标角度
9. φ:球坐标角度
对应输出量为该体素对应的临床计划接收的物理剂量。
其中,体素距离与角度信息需要通过MATLAB计算获得。计算过程如下:首先计算目标结构的距离场,计算距离场在相应器官的0-1二值矩阵中进行,即在一固定维度大小矩阵中把对应位置属于该器官的体素值置为1,否则置为0。再利用距离场算法计算其距离场矩阵,并标记其边界上体素的距离为零,结构内的距离标记为负,结构外的距离标记为正。其中应用快速欧几里得距离算法[17]可有效提高该部分的计算效率。图 2显示了一例患者的PTV和OAR的结构及其距离场的一个横截面,从左到右对应结构分别为膀胱、直肠、股骨头和PTV(前列腺),第二行为对应的距离场灰度图,白色代表距离值越大,黑色代表值越小。从距离场中可以得到目标体素的距离信息和角度信息。

|
图 2 PTV和OAR的结构及其对应距离场的横截面示例 Figure 2 An example of structure of the PTV and OAR and the cross section of the distance field. |
本文以前列腺癌IMRT计划的OAR作为感兴趣区域建立三维剂量分布预测模型。不同的ROI具有不同的相对位置,以及不同的剂量分布情况。因此本文为膀胱、直肠和股骨头3种OAR分别建立神经网络训练模型,结构与输入输出特征相同。
神经网络结构为前馈反向传播网络,包含五层网络层,分别为1个输入层、3个隐藏层和1个输出层。输入层与隐藏层分别含有9个节点,输出层1个节点,图 3显示了神经网络的拓扑结构。

|
图 3 前馈反向传播神经网络拓扑结构 Figure 3 Feed forward back-propagation neural network topology. |
应用MATLAB的nntool工具包可以高效建立和训练模型,以及调整参数,查看训练情况。神经网络利用输出值与目标值的均方误差求得反向传播梯度用以调整每个网络层节点的权重值和偏差值[18-19],以及使用Levenberg-Marquardt[20]算法寻求最优解。Tan-sigmoid函数为非线性函数适合非线性数据拟合,因此适用于神经网络隐含层[21-22],输出层需要实现回归功能因此应用线性函数。神经网络的所有输入与输出数据,输入为9维特征,输出为对应体素剂量(具体见1.3输入特征)。每个体素剂量计算后将重新组合成三维剂量分布矩阵。
1.5 模型训练与验证数据集按照80%和20%分别作为训练和验证批次,多次迭代用以降低个别奇异样本对整体模型的精度影响。为避免过拟合,当连续6个迭代周期内均方误差不再减少或迭代次数超过1000次时,停止训练。
为验证网络鲁棒性和稳定性,分别对每一个OAR的神经网络进行4次训练,训练数据随机更换不同病例,分析训练误差和训练集样本DVH判断神经网络性能。在验证阶段,预测集数据作为神经网络输入,通过网络计算得到预测剂量值,并分析模型预测与临床计划三维剂量分布之间的差异,对比两者DVH,验证模型性能。
随机选取20例计划为训练集,其余5例为测试集,即三种OAR模型分别有20例训练,5例测试,针对不同OAR数据分别进行训练和验证。模型训练数据量为10~50万左右,数据计算前分别进行归一化处理以提高网络收敛速度和增加稳定性。
本研究使用三维剂量分布的点对点平均剂量差异值(简称剂量差异)描述三维剂量分布的剂量差异;DVH中固定剂量序列各对应的相对体积值的差的平均(简称DVH差异)作为DVH差异描述。
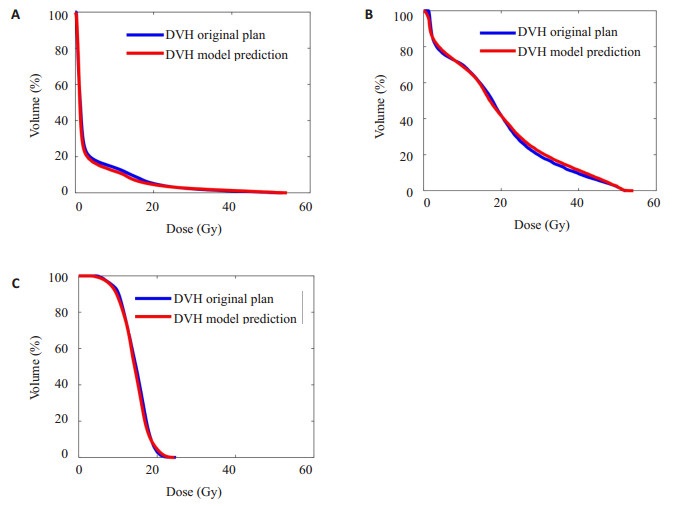
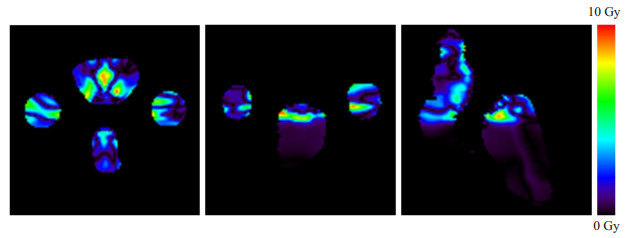
2 结果 2.1 模型训练结果对3个模型分别进行了4次训练,其训练样本剂量差异如表 1所示,剂量差异在-0.092±3.673 Gy到0.089± 4.072 Gy之间,百分剂量差异不超过0.2%。3个模型训练样本DVH差异均值分别为1.15%,1.63%和1.33%,差异值较小,模型间训练样本结果差别不大。一例训练样本的临床计划与模型预测DVH比较如图 4所示,其中,蓝线是原始计划DVH,红线是模型预测DVH,从左到右分别为膀胱、直肠和股骨头。DVH差异分别为0.79%, 1.04%和0.98%,DVH差异较小。该训练样本三维剂量差异分布图的三视图截面如图 5所示,总体剂量差异为-0.143±3.275 Gy,最大剂量差异不超过10 Gy。
| 表 1 3种模型的训练样本剂量差异结果 Table 1 Training error of 3 models (Gy) |
|
图 4 一例训练集样本临床计划与模型预测的DVH比较,从左到右(A)-(C)分别为膀胱、直肠和股骨头 Figure 4 Comparison of DVH in the original plan and the predicted DVH by the model in a sample. |
|
图 5 一例训练集样本绝对剂量差异分布图的三视图截面 Figure 5 Three views of the absolute dose difference distribution a training in a training sample. |
预测集样本中,膀胱的剂量差异为0.614 ± 6.956 Gy,直肠为0.380±10.199 Gy,股骨头为1.369± 14.563 Gy,膀胱和直肠相对股骨头差异较小,模型预测效果更好。3个模型预测样本DVH差异分别为2.31%,3.18%和3.94%,膀胱模型预测样本DVH差异较小,直肠和股骨头次之。
5例验证集样本剂量差异分别为-0.352±10.678 Gy,1.214±11.550 Gy,1.016±10.222 Gy,-1.201±11.257 Gy,0.143±9.425 Gy,百分剂量差异在2.5%以内,预测集样本总体剂量差异为0.163±10.525 Gy,总体预测效果较好。
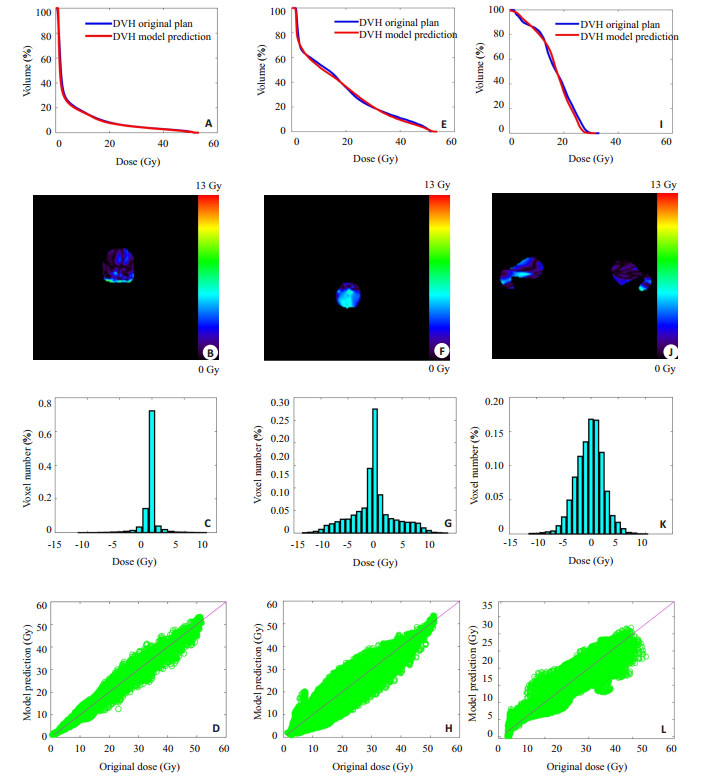
图 6从左到右分别展示了一例预测样本中膀胱、直肠和股骨头的剂量差异情况。从上到下分别为DVH对比,三维剂量差异分布,差异量化情况和剂量符合情况。对于DVH比较图,蓝线是临床计划DVH,红线是模型预测DVH。3个器官DVH差异分别为1.22%,2.48%,2.76%,且红蓝两者形状接近,差异较小,DVH结果较为准确。第二行展示的是剂量差异绝对值的三维分布截面,三个器官剂量差异最大值不超过13 Gy,剂量差异分别为0.261±3.184 Gy,-0.361±8.154 Gy,1.663± 10.812 Gy,总体剂量差异较小,膀胱相比直肠和股骨头方差较小。第三行图表示模型预测和临床计划剂量之间的剂量差异分布量化情况,横坐标为剂量差异值,纵坐标为对应差值范围的体素数量,差异值均集中在0值附近,两侧呈对称分布。第四行表示模型预测和临床计划剂量值的符合情况,横坐标和纵坐标分别表示临床计划剂量值和模型预测剂量值。坐标点越靠近y=x的紫色对角线,表明预测值越准确,其中大部分点都集中在对角线上,膀胱和直肠模型预测剂量准确度优于股骨头。
|
图 6 从左到右分别为来自膀胱,直肠和股骨头模型的一例预测结果剂量对比情况 Figure 6 Comparison of the predicted doses of the bladder, rectum, and femoral heads (from left to right). |
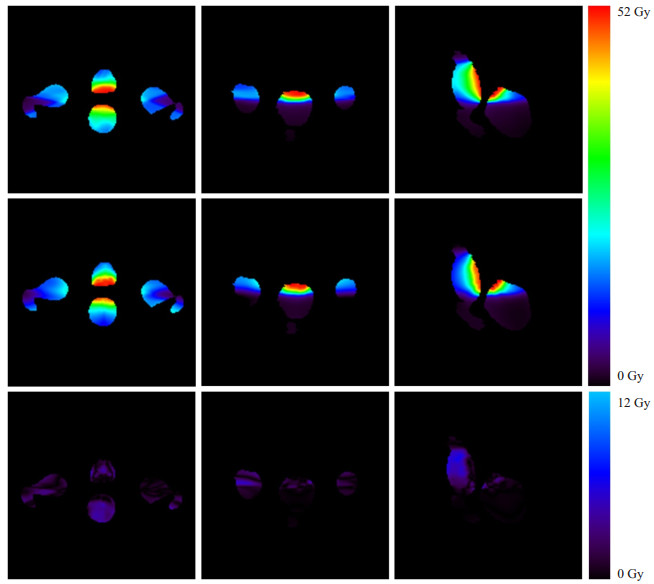
另一例预测样本的三维剂量分布及其剂量差异分布情况,如图 7所示,从上到下分别为临床计划、模型预测和两者间点对点剂量差异绝对值的三维剂量分布三视图截图。其中样本剂量差异为-0.352±10.678 Gy,总体剂量差异较小,剂量分布合理。
|
图 7 1例预测样本临床计划与模型预测三维剂量分布比较 Figure 7 Three-dimensional dose distribution in the original plan and predicted by the model in a sample. |
模型训练结果表示,训练集的剂量差异,即三维计量分布点对点的模型预测剂量值与临床计划剂量值差异均值,在-0.092±3.673 Gy到0.089±4.072 Gy之间,训练样本的剂量差异较小。模型预测DVH与临床计划DVH相比差异较小,DVH差异在2%以内,数据拟合效果理想。利用预测模型对未参与训练数据进行预测,预测样本百分剂量差异在2.5%以内,误差分布集中在0值附近,呈现对称分布,模型预测效果较好。其中膀胱模型预测效果最佳,直肠和股骨头模型次之。从危及器官结构形状可以看到,膀胱体素分布类似球型,结构相对紧凑,而直肠和股骨头的体素相对于膀胱体素分布较为不规则,训练数据中包含的距离范围与角度范围更广,在训练集数据某一范围内,数据量相对较少。对于同类型的放疗计划,属于在同一种OAR的体素,会有类似的剂量分布,相对较少的数据量对于神经网络训练会造成过拟合[16, 23],预测结果也会产生偏差。膀胱体素的训练数据量在50万左右,相对直肠和股骨头10万左右训练数据更不容易出现过拟合现象,因此膀胱模型表现相对较好。
相对于直接预测感兴趣区域(ROI)的DVH,本文通过神经网络直接预测三维剂量分布,能得到ROI的所有体素剂量,相应DVH也能随之计算出来。DVH是一维数据,缺乏体素位置信息,存在不同的剂量分布也能得到相同DVH的情况,具有不确定性,而得到每个体素的剂量信息,保留了空间位置信息,体素剂量与位置关系一一对应,具有确定性,且能提供更丰富的剂量指征信息。
通过预测得到三维剂量分布得到参考约束目标,作为放疗计划设计与优化初始条件,能为计划自动设计和计划质量控制提供更多帮助[10-11]。理论上训练样本足够优秀和足够丰富以及拥有合适的训练模型,其预测所得到的值相当于经验丰富的人类工作者计算得到的结果,优秀模型预测值能包含经验丰富的人类工作者对该项任务的经验[24-25]。神经网络的结构模仿人的大脑,各层节点连接权值与偏差值存储着从训练数据中学习到的特征知识[19],经过神经网络计算的三维剂量分布接近经验丰富的计划者所得出的计划剂量分布,为放疗计划自动生成与质量控制提供基础。
若探讨预测整个照射区域所有体素剂量分布,数据量会变得非常大,训练数据量在亿数量级,网络将会变得异常庞大,且网络训练效率低下,传统神经网络难以准确计算所有体素剂量。尝试将整个受照射区域分开若干计算区域建立模型,再把各个区域重组得到三维剂量矩阵是一个较好的解决方法,但此方法会产生每个计算区域过渡不均匀,剂量在区域边界存在较大梯度,造成总体剂量分布不平滑等问题。医学图像分割网络U-Net[26]通过深度卷积网络,可对医学图像进行准确分割,基于其深度卷积网络特性,可修改网络结构使得U-Net能够训练放疗计划数据,并获得剂量预测模型。即通过深度学习[27]方法预测整个照射区域剂量分布,把CT图像、ROI轮廓和剂量分布等信息作为训练数据,训练深度神经网络,直接通过深度网络生成二维或三维的剂量分布,该模型在以后的工作中会有进一步的研究探讨。
综上所述,本文提出了一种基于神经网络学习方法的放疗计划三维剂量分布预测方法。为验证该方法,本研究收集了25例前列腺癌IMRT/SBRT计划,并从临床数据中提取了相应的空间位置信息、体积信息和剂量特征,应用搭建的前馈反向传播神经网络构建了三维剂量预测模型。
| [1] |
胡逸民.
肿瘤放射物理学[M]. 北京: 原子能出版社, 1999.
|
| [2] |
Webb S.
Intensity-modulated radiation therapy[M]. CRC Press, 2001.
|
| [3] |
Miles EA, Clark CH, Urbano MT, et al. The impact of introducing intensity modulated radiotherapy into routine clinical practice[J].
Radiother Oncol, 2005, 77(3): 241-6.
DOI: 10.1016/j.radonc.2005.10.011. |
| [4] |
Fredriksson A. Automated improvement of radiation therapy treatment plans by optimization under reference dose constraints[J].
Phys Med Biol, 2012, 57(23): 7799-811.
DOI: 10.1088/0031-9155/57/23/7799. |
| [5] |
Chung HT, Lee B, Park E, et al. Can all centers plan intensitymodulated radiotherapy (IMRT) effectively? An external audit of dosimetric comparisons between three-dimensional conformal radiotherapy and IMRT for adjuvant chemoradiation for gastric cancer[J].
Int J Radiat Oncol Biol Phys, 2008, 71(4): 1167-74.
DOI: 10.1016/j.ijrobp.2007.11.040. |
| [6] |
Nelms BE, Robinson G, Markham J, et al. Variation in external beam treatment plan quality: An inter-institutional study of planners and planning systems[J].
Pract Radiat Oncol, 2014, 2(4): 296-305.
|
| [7] |
Wu B, Ricchetti F, Sanguineti G, et al. Patient geometry-driven information retrieval for IMRT treatment plan quality control[J].
Med Phys, 2009, 36(12): 5497-505.
DOI: 10.1118/1.3253464. |
| [8] |
Zhu X, Ge Y, Li T, et al. A planning quality evaluation tool for prostate adaptive IMRT based on machine learning[J].
Med Phys, 2011, 38(2): 719-26.
DOI: 10.1118/1.3539749. |
| [9] |
李航.
统计学习方法[M]. 北京: 清华大学出版社, 2012.
|
| [10] |
Mcintosh C, Purdie TG. Voxel-based dose prediction with multipatient Atlas selection for automated radiotherapy treatment planning[J].
Phys Med Biol, 2017, 62(2): 415-31.
DOI: 10.1088/1361-6560/62/2/415. |
| [11] |
Wang H, Dong P, Liu H, et al. Development of an autonomous treatment planning strategy for radiation therapy with effective use of population-based prior data[J].
Med Phys, 2017, 44(2): 389-96.
DOI: 10.1002/mp.12058. |
| [12] |
Yuan L, Ge Y, Lee WR, et al. Quantitative analysis of the factors which affect the interpatient organ-at-risk dose sparing variation in IMRT plans[J].
Med Phys, 2012, 39(11): 6868-78.
DOI: 10.1118/1.4757927. |
| [13] |
Shiraishi S, Moore KL. Knowledge-based prediction of threedimensional dose distributions for external beam radiotherapy[J].
Med Phys, 2016, 43(1): 378.
|
| [14] |
Appenzoller LM, Michalski JM, Thorstad WL, et al. Predicting dose-volume histograms for organs-at-risk in IMRT planning[J].
Med Phys, 2012, 39(12): 7446-61.
DOI: 10.1118/1.4761864. |
| [15] |
Skarpman Munter J, Sjölund J. Dose-volume histogram prediction using density estimation[J].
Phys Med Biol, 2015, 60(17): 6923-36.
DOI: 10.1088/0031-9155/60/17/6923. |
| [16] |
周志华.
机器学习[M]. 北京: 清华大学出版社, 2016: 97-107.
|
| [17] |
Mishchenko Y. A fast algorithm for computation of discrete Euclidean distance transform in three or more dimensions on vector processing architectures[J].
Signal Image Video Proc, 2015, 9(1): 19-27.
DOI: 10.1007/s11760-012-0419-9. |
| [18] |
Rumelhart DE, Hinton GE, Williams RJ. Learning representations by back-propagating errors[J].
MIT Press, 1988, 323(6088): 533-6.
|
| [19] |
Lecun Y, Bengio Y, Hinton G. Deep learning[J].
Nature, 2015, 521(7553): 436-44.
DOI: 10.1038/nature14539. |
| [20] |
Kanzow C, Yamashita N, Fukushima T. Levenberg-Marquardt methods with strong local convergence properties for solving nonlinear equations with convex constraints[J].
J Comput Appl Math, 2004, 172(2): 375-97.
DOI: 10.1016/j.cam.2004.02.013. |
| [21] |
Cybenko G. Approximation by superpositions of a sigmoidal function[J].
Mathematics of Control Signals and Systems, 1989, 2(4): 303-14.
DOI: 10.1007/BF02551274. |
| [22] |
Leshno M, Lin V, Pinkus A, et al. Multilayer feedforward networks with a Non-Polynomial activation function can approximate any function[J].
Neural Networks, 1993, 6(6): 861-7.
DOI: 10.1016/S0893-6080(05)80131-5. |
| [23] |
Srivastava N, Hinton G, Krizhevsky AA, et al. Dropout: a simple way to prevent neural networks from overfitting[J].
J Machine Learning Res, 2014, 15(1): 1929-58.
|
| [24] |
Mnih V, Kavukcuoglu K, Silver D, et al. Human-level control through deep reinforcement learning[J].
Nature, 2015, 518(7540): 529-33.
DOI: 10.1038/nature14236. |
| [25] |
Silver D, Huang A, Maddison CJ, et al. Mastering the game of Go with deep neural networks and tree search[J].
Nature, 2016, 529(7587): 484-9.
DOI: 10.1038/nature16961. |
| [26] |
Ronneberger O, Fischer P, Brox T. U-Net: Convolutional networks for biomedical image segmentation[C]. International Conference on Medical Image Computing and Computer-Assisted Intervention. Springer, Cham, 2015: 234-41.
|
| [27] |
Goodfellow I, Bengio Y, Courville A.
Deep learning[M]. Cambridge: MIT Press, 2016: 326-65.
|
 2018, Vol. 38
2018, Vol. 38

