2. 广东省医学图像处理重点实验室,广东 广州 510515
2. GuangdongProvincial Key Laboratory of Medical Image Processing, Southern Medical University, Guangzhou 510515, China
多种模态的核磁共振成像(MRI)能很好地揭示正常组织和肿瘤的结构区别[1]。目前,胶质瘤是成年人最常见的原发性脑胶质瘤。为了在治疗前后使用神经影像学评估疾病的进展和治疗策略的成效,需要对肿瘤基础结构进行高精度、可重复的测量评估。分割脑胶质瘤作为必要的步骤,病变区域的轮廓只能通过像素灰度相对与周围组织的变化确定且较多MR图像带有灰度偏移场使得轮廓难以精准划分。此外,肿瘤的结构在大小、延展和定位上的差异使得分割算法在形状和位置参数无法使用类似正常组织的强先验约束[2]。上述因素使得精准地手动分割脑质瘤成为一项必要但费时费力的工作,因此研究如何提升自动分割脑胶质瘤方法的精度是一个很有意义的工作。随着人工智能和深度学习的兴起,相比于传统手工设计图像特征的方法[3-5],基于卷积神经网络(CNN)的分割算法[6-9]在脑胶质瘤分割中有着不错的性能。我们将最近性能最好的通用分割网络之一全卷积DenseNet[10]从自然图像迁移至脑胶质瘤数据集。
为了能更有效地提高肿瘤区域的分割精度,本研究做了以下三个方面的创新和改进。(1)脑胶质瘤数据集相比大多自然图像数据集和一些医学图像数据集具有更严重的类不平衡性,影响网络参数的学习。大多数学者往往简单地使用Dice损失函数[11-13]进行缓解,但效果提升甚微。为了有效缓解类不平衡,针对脑胶质瘤的分割任务,我们对损失层进行了创新,提出了多Dice损失函数的结构。该结构由3个Dice损失层构成,直接对应了3个需要分割的目标区域,不同于单损失函数对应于这些区域的子区域而只能间接优化目标的分割。另外,单损失函数优化肿瘤子区域的分割使得原本严重的类不平衡性更进一步放大。本文提出的结构是对子区域的合集进行分割,直接从根源上降低了分割目标的类不平衡性。文献[14]虽然有部分类似想法,但多个网络逐步训练导致效率低下。本文的方法只需修改损失层,易于操作且提升了分割精度。(2)不同于常用的softmax损失函数是基于像素点,Dice损失函数是一种基于区域的损失函数。网络训练时,每批训练数据的图像块单独计算损失函数不同于图像块合并计算损失函数。很多文献并没有指明这细节,我们补充了这部分实验。(3)对于最后的标签融合步骤,我们采用不同的步长进行实验。
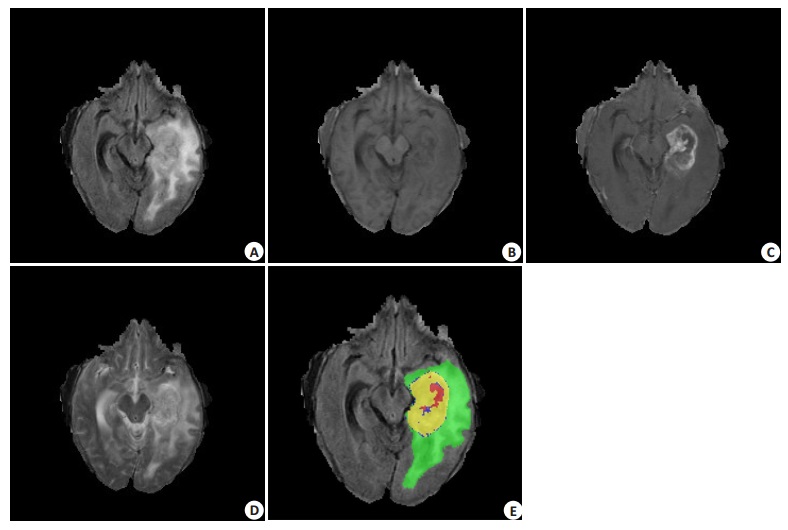
1 资料和方法 1.1 实验数据我们使用2015年多模态脑肿瘤分割挑战赛[2](BraTS)的数据进行训练和测试。BraTS是一个全球性质的比赛,其训练集包括220例高级别胶质瘤与54例低级别胶质瘤及对应的组织分割图像。测试集包括110例胶质瘤数据,但未提供更详细的肿瘤分级与对应的分割图像。脑胶质瘤(图 1F)共分为以下4类:(1)显示为红色区域的坏死组织;(2)显示为绿色区域的水肿;(3)显示为蓝色区域的未增强肿瘤;(4)显示为黄色区域的增强肿瘤。为了评估分割的优劣,4中不同的组织被组合成3个集合:(1)整个肿瘤,即所有类;(2)肿瘤核心区,由坏死组织、未增强肿瘤和增强肿瘤组成;(3)肿瘤增强区,仅由增强肿瘤组成。测试集是不公开的,仅能采用在线上传的评估方式(https://www.smir.ch/BRATS/Start2015)。每个病例包括Flair(图 1A)、T1(图 1B)、T1增强(图 1C)、T2(图 1D)共4种MRI模态。它们是由多达19种不同的扫描设备配置和机构提供。MRI数据均配准至相同的图像空间并去除头骨部分。每个图像的大小为240×240×155,分辨率重采样至1 mm×1 mm×1 mm,且所有的图像标签均由1至4个专家手动分割。
|
图 1 BraTS2015数据集的例子 Figure 1 The CaseinBraTS2015 dataset. A: Flair; B: T1: C: T1 enhanced image; D: T2 and (E) the corresponding expert segmentation result. |
MR图像往往由于磁场的不均匀性,导致图像灰度的偏移。比如在[3]中执行的图像预处理操作为用N3算法[15]来校正MR图像中的灰度偏移场再进行归一化,但这可能会移除掉部分原始有用的信息。在我们的方法中,为了最大限度保留原始信息,仅仅进行最少的预处理操作。我们直接对每个图像内的脑组织灰度进行0均值,1方差的归一化操作。
为了减少无效的图像信息,我们分别生成二维和三维两种数据。二维的数据大小为208×208,并去除脑组织周围大量的0值背景像素,且只选择有肿瘤数据存在的图像层作为训练数据。三维的数据大小为32×32× 32,我们采用类似[14]的方案采样训练数据。每个病例采样70个图像块,每个图像块的中心体素按照以下概率进行随机选取:背景占1%、正常组织占29%、肿瘤组织占70%。
1.3 基础的网络结构DenseNet[16]以及其分割版本全卷积DenseNet[10]一种能够对图像特征进行重用的神经网络结构。不同于GoogleNet[17]、ResNet[18]等其他网络,这些网络只是前向地从上一层的特征中学习更高层次的特征,抽象低层次的特征后便舍去。换而言之,每一层的特征在整个网络中大多只使用1次。特征的重用率低下导致网络的学习效率难以提高。虽然在深度学习研究火热的现在,研究人员一直致力于层数更深的网络的研究,但一味地提升网络深度而没有提高特征的使用率也是意义不大。
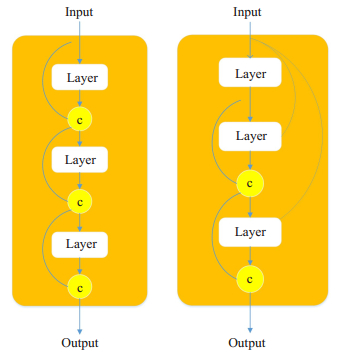
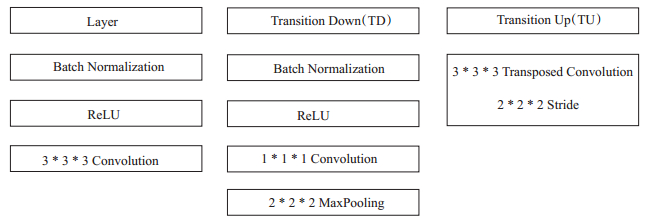
为了提高特征的使用效率,研究人员对网络学习到的每层特征进行重用,每一层网络的输入包括前面所有层学习到的图像特征(图 2)。具体地,FC-DenseNet结构由以下几部分(图 3)组成:由多个层级联而成的密集连接块(DB)和两种过渡层(TL):参考目前在医学数据上训练成功的神经网络结构,U-Net[19]有4个下采样层,每个下采样层之间由2个3 × 3的卷积层组成;DeepMedic[9]有8个3×3×3的卷积层。因此我们将基础网络的结构设置为下采样通路和上采样通路均由3个DB与对应的采样操作组成,每个DB有4个卷积层组层,两个采样通路由1个DB连接,网络的最初输入特征图数目和增长率分别为48和12。该网络(DB-3-Layer- 4)在三维结构中的具体细节如图 4所示。我们将这个网络结构称为DenseNet_Base。
|
图 2 密集连接块的两种结构 Figure 2 Two structures of dense block. |
|
图 3 全卷积DenseNet的组成单元 Figure 3 The block unit of full convolutional DenseNet. |

|
图 4 我们实验使用的基础全卷积DenseNet的3维结构细节 Figure 4 3D architecture details of basic FC-DenseNet model used in our experiments. |
为了比较三维网络结构在医学数据上比二维网络结构更能提取有效信息,我们进行二维全卷积DenseNet_Base和三维全卷积DenseNet_Base的比较实验。
该实验中,我们采用逐像素的softmax交叉熵作为网络的损失层函数。训练基于梯度下降算法,采用Nadam进行加速梯度下降,学习率设置为3e-5,卷积权重采用L2范数正则化,正则化系数为1e-4。在计算内存条件允许的情况下,根据二维和三维图像数据大小的不同选择网络训练能接受的合适数据量。由于是基础网络,为了能得到一个各种结构的比较基准,我们各花费近一星期时长运行200轮的迭代,直至分割精度几乎不提升。我们所有实验使用的计算硬件为一块NVIDIATitanX显卡,软件包基于tensorflow[20]的keras。
1.4.2 不同步长的标签融合的比较在图像块进行标签融合而生成最终的脑肿瘤区域分割图像时,不同的步长参数是否能显著提高脑肿瘤数据的分割精度?基于这个疑问,我们使用实验1.4.1节中训练好的三维全卷积DenseNet_Base进行肿瘤区域类别的预测。在同一个模型下,分别采用步长32、步长16以及步长8进行对比实验。因为数据块的边长为32,所以只有步长不大于32时才能保证每个图像像素点都进行区域分类。标签融合采用最简单的概率平均融合。具体地,步长为32像素、16像素和8像素的每个像素点概率分别是由1个、8个和64个概率平均得到。
1.4.3 不同计算步骤的损失函数的比较以往的多分类损失函数经常选择的是交叉熵(CE)损失函数,其损失值由以下公式计算得到:
| $ CE\left( {g,p} \right) = - \sum\nolimits_{i = 1}^v {{g_i}\;{\rm{log}}\;{p_i}} $ | (1) |
其中g代表真实值(groundtruth),p代表网络的预测概率值(predictedprobability),v代表每个图像块的像素点个数。
对于每一批训练数据,假设每次共有m个图像块输入网络,即网络共输出mv个像素点,其每次的损失值为:
| $ CE\left( {g,p} \right) = - \sum\nolimits_j^m {\sum\nolimits_{i = 1}^v {{g_{ji}}\;{\rm{log}}\;{p_{ji}}} } = \sum\nolimits_k^{mv} {{g_k}\;{\rm{log}}\;{p_k}} $ | (2) |
从上式可以看出,对于交叉熵损失函数,先计算每个图像块的损失值后再进行求和,等价于直接计算每个图像像素的损失值的和。然而这对于Dice损失函数却是不等价的。目前的分割任务常采用Dice相似性系数(DiceSimilarityCoefficient)作为分割精度的客观评估指标,其定义为:
| $ Dice\left( {A,B} \right) = \frac{{2 \times \left( {A \cap B} \right)}}{{A + B}} $ | (3) |
其中A和B分别代表算法分割的脑肿瘤区域和专家手动分割的真实脑肿瘤区域,A ∩ B代表算法的分割区域与专家手动分割区域交集部分的体素区域,A ∪ B代表算法的分割区域与专家手动分割区域并集部分的体素区域。由于Dice相似性系数不能进行网络输出误差的反向传播,也就无法作为损失函数。近年,不少学者对Dice相似性系数进行改进,提出Dice损失函数,其形式通常有一次方形[11-12]和二次方形式[13]。我们在本实验中采用的是后者,其定义为:
| $ Dice\left( {g,p} \right) = 1 - \frac{{2\sum\nolimits_i^v {{p_i}{g_i}} }}{{\sum\nolimits_i^v {\left( {p_i^2 + g_i^2} \right)} }} $ | (4) |
在尝试类似于交叉熵损失函数的计算后,可以发现对于Dice损失函数,先计算每个图像块的损失值后再进行求和,与直接计算每个图像像素的损失值的和,这两者是不等价的,也就是如下的不等式:
| $ \sum\nolimits_j^m {\frac{{2\sum\nolimits_i^v {{p_{ij}}{g_{ij}}} }}{{\sum\nolimits_i^v {\left( {p_{ij}^2 + g_{ij}^2} \right)} }}} \ne \frac{{2\sum\nolimits_k^{mv} {{p_k}{g_k}} }}{{\sum\nolimits_k^{mv} {\left( {p_k^2 + g_k^2} \right)} }} $ | (5) |
我们将左边的Dice公式记为Dice_E(Each Instance),将右边的Dice公式记为Dice_A(All Instances)。为了比较这两者对于网络训练的差别,同时也与交叉熵损失函数进行比较,我们在DenseNet_Base的结构上分别采用这3种损失函数。网络的具体训练参数与1.4.1节的参数大同小异,其中网络训练的轮数有所减少。我们观察训练中的分割结果,在觉得可以说明3者的差别时便停止网络训练,最终各网络运行18轮的迭代。在标签融合时,采用16像素的步长。
1.4.4 单损失函数和多损失函数的比较对于脑胶质瘤的分割任务,与其他常见的自然图像分割任务有一定的区别。(1)BraTS2015数据集具有更严重的类不平衡性。(2)BraTS2015数据集的每类病变组织区域更难精准分割。(3)BraTS2015的分割任务与一般类别较少的自然图像分割任务具有明显的不同之处,也是最为主要的不同之处。在许多类别较少自然图像中,每类区域往往都是独立的。目标一般是对各类区域精准分割,任务关注的往往是整个自然图像,各个区域也较少进行合并后再评价。Dice损失函数是一种对每个区域独立评价后对网络参数进行反馈的函数,其函数的形式和计算过程都很好地契合这类自然图像的分割目标,因此取得较高的性能评估值。然而BraTS2015的目标是3类具有从属关系的肿瘤区域的精准分割,这使得Dice损失函数对其数据集勾画的5类区域进行精准地分割只能间接地提升目标的分割精度。在3类目标区域中,整个肿瘤区比肿瘤核心区增加水肿组织一类,肿瘤核心区比增强肿瘤区增加坏死组织和非增强组织两类。水肿组织是相对容易分割的目标,但坏死组织和非增强组织是网络分割较差的目标。目前好的损失函数会符合一个人的直观感受:网络较难判断即误差较大的目标,网络误差回传的梯度也会较大,反之亦然。也就是说,网络参数会优先朝着难以辨别的目标进行优化。对交叉熵进行求导计算便可以发现其具有这一性质。Dice损失函数可以视为加权的交叉熵函数,我们假设其也具有这一性质。从这可以推导出,直接使用原始的Dice损失函数会使得网络参数更多地朝着较难分割的坏死区域和非增强区域进行优化。这两个区域在这种情况下又难以分割,使得其他区域的优化受到一定的限制,不利于对BraTS2015的3类目标进行更精准的分割。
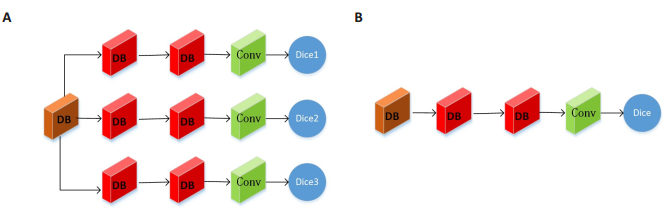
简而言之,同一个卷积核需要有能区分所有区域特征的能力,这对于仅有灰度值特征且边界也模糊不清的脑肿瘤精准分割,是很有难度的。针对单卷积核学习多区域特征的难点,我们改进网络最后几层的结构,如图 5所示。具体地,我们在DenseNet_Base的最后一个DB后并行添加3个网络结构分支。每个分支分别由一个2层的DB结构接一个1×1×1的卷积核组成,分别对应于BraTS2015数据需要分割的整个肿瘤区、肿瘤核心区和肿瘤增强区3个区域。添加的DB结构,是为了能在DenseNet_Base对所有的肿瘤区域共同进行特征抽取后,独立地对每类肿瘤区域进行特征的精炼,得到更具有辨别性的图像特征。每个分支采用1.4.3节中的Dice_E作为损失函数,并将该网络记作DenseNet_MD_E(Multi-Dice loss function for Each Instance),如图 5A。作为比较的网络结构,我们并不是直接采用DenseNet_Base作为基准。因为我们的每个网络分支比原始结构各增添一个DB,并不能排除网络分割性能的改变是由于添加DB结构。为了能公平地体现多损失函数的作用,我们在DenseNet_Base的基础上同样添加一个同参数的DB结构,损失函数同样采用Dice_E,并将该比较网络记作DenseNet_SD_E(Single-Dice loss function for Each Instance)如图 5B。虽然以往也有学者[14]采用一个Dice损失函数对应一类肿瘤区域,但是其使用多个网络进行训练,即3类区域就有3个甚至更多的网络,大大增加网络的参数和预测的时间。
|
图 5 多Dice损失函数和单Dice损失函数的结构图 Figure 5 Structure of multi-Dice loss function (A) and single-Dice loss function (B). |
由于网络结构的增加,每轮的训练时间也同样增加不少。因此本实验在采用1.4.1节的训练参数时,将网络的训练轮数减少为100轮,并没有训练至网络分割精度不再增加。在标签融合时,采用16像素的步长。
1.4.5 多参数优化的实验对于三维的全卷积DenseNet,以更大的图像块作为输入往往能带来一定的精度提升。但更大的图像块也意味着更大的计算开销,对于三维数据来说更为严重。本文的实验数据来源于一个全球挑战赛,为了能提升分割精度并与其他方法进行比较,我们采用以下策略:对原始病例进行水平翻转的数据增强后,采集图像块大小为64像素的数据集,并采用步长为1的标签融合方式,在单GPU下进行十多天的网络训练。
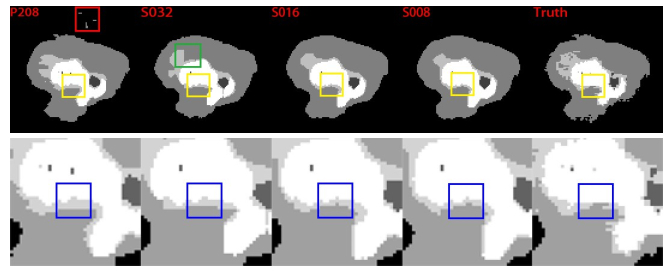
2 结果 2.1 二维DenseNet_Base和不同步长下的三维DenseNet_Base的肿瘤区域分割结果图 6从左到右分别是二维DenseNet_Base网络分割结果P208(Patch Size=208)、三维DenseNet_Base分割结果S032(Stride=32)、S016(Stride=16),S008(Stride= 8)的分割结果和专家分割的结果(Truth)。第1行是整个的分割结果图,第2行是第1行中同一个区域的局部放大图,我们将同一区域用黄色框来表示。表 1是该4种实验和他人方法的分割精度的定量指标以及同设备下的计算时间。从视觉感受以及定量指标均可以看出在分割精度上三维结构优于二维,且融合步长越小精度越高,但计算时间越长。通用二维网络的分割精度为82.4%、66.5%和61.1%,在考虑了医学数据三维特性后的网络分割精度达到了83.4%、69.2%和62.9%。在针对脑胶质瘤数据集特点而引入了多Dice损失函数并进行数据扩增,分割精度达到了85.1%、71.2%和63.0%(表 1)。
|
图 6 4种方法的分割结果与实际的分割图像 Figure 6 Segmentation result of 4 methods and the ground truth. |
| 表 1 脑肿瘤分割算法的Dice系数的均值比较 Table 1 Comparison of mean Dice value of brain tumor segmentation algorithms |
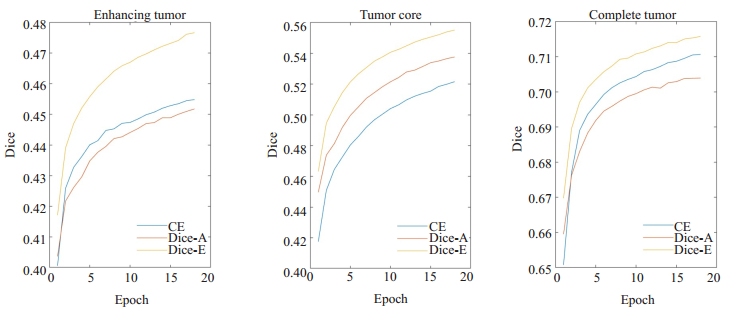
3种不同的损失函数CE、Dice_E和Dice_A在训练过程对整个肿瘤区、肿瘤核心区以及增强肿瘤区的分割结果如图 7所示(此处的Dice系数是由图像块而不是整幅图像计算得到,所以和2.1节的Dice值有一定的差异)。从训练曲线可以看出,在三种区域的分割精度上,Dice_E都显著优于Dice_A和CE,特别是肿瘤核心区的分割精度提高最明显。具体地,在整个肿瘤区、肿瘤核心区以及增强肿瘤区的Dice系数分别提高0.012和0.005、0.017和0.034、0.024和0.022。
|
图 7 不同损失函数的分割结果 Figure 7 Segmentation results for different loss functions. |
我们在测试集上分别评估采用单Dice损失函数和多Dice损失函数的网络结构的分割结果,Dice系数如表 2所示。整个肿瘤区的分割,两者几乎没差异;但是在肿瘤核心区的分割中,多损失函数带来接近0.01的提升;增强肿瘤区的分割精度提升较小,只提高0.005。
| 表 2 单Dice函数和多Dice函数的分割结果 Table 2 Segmentation results of single-Dice function and Multi-Dice function |
我们将未进行优化的最初结构与本文改进后的网络结构以及其他的一些学者针对同一个数据集BraTS2015提出的方法的实验结果数据罗列在表 3中。我们从这些量化的评估结果可以看出本文的方法的确能有效提升BraTS2015的分割性能,与一些优秀的算法不相上下,甚至有所提高。在网上测试平台中,该优化后的分割结果总排名第6,其中整个脑肿瘤区、肿瘤核心区以及肿瘤增强区的Dice分割精度排名分别为第4名、第8名和第9名。
| 表 3 不同算法的Dice系数的均值比较 Table 3 Comparison of mean Dice value of different algorithm |
随着精准医疗的提出和完善,精确的定量分析相比简单的定性分析能起到更好的作用。虽然使用越来越精准的通用分割方法或者结构能带来脑胶质瘤分割精度的提升,但只有针对脑胶质瘤数据集的特性进行设计才能使得分割精度超越通用方法而进一步提高。
本研究利用深度学习的方法,使用274例脑胶质瘤患者(包括220例高级别脑胶质瘤和54例低级别脑胶质瘤)进行深度网络的参数训练,对另外110例脑胶质瘤(未区分恶性程度)的整个脑胶质瘤、肿瘤核心区以及增强肿瘤区进行分割,以检验该方法的分割泛化性,使得分割精度提高。
三维结构是医学数据相比自然图像的一大特性,使用三维结构能更好地利用图像体素周围的组织灰度关系。虽然Zhao[21]采用了二维的图像层取得了不错的分割结果,但其分别使用矢状面、冠状面、横切面的数据训练3个网络并进行融合。这与直接使用三维图像块没有显著区别,同时增加网络的训练时长。三维网络结构使训练时间大幅增加,但生成分割图像的时间相比传统方法[3-4]仍较短。由于当前显存技术的限制,本研究无法输入整个三维图像。采用较小图像块的输入方式后,需要对输出图像块进行拼接融合操作。较小的融合步长能带来分割精度的提升,但也使得预测时间大幅增加。
分割目标的像素稀少是脑胶质瘤分割任务不同于正常组织分割的一个特点,这对于目标区域最小的增强肿瘤区更为明显,限制了区域分割精度的提升。Dice损失函数[22]可以看作是对每个像素点的加权求和。当区域越小时,权重就相对越大,这样便有效缓解分割任务中各类区域的类不平衡问题[13],特别是背景大而前景小的肿瘤分割。不同的Dice损失值计算方式也会影响网络的学习性能。比如当某一批训练数据中,肿瘤核心区大小差别较大,而靠近边界的区域更难预测导致小的区域比大的区域更难精准地分割。采用合并计算会导致区域小的样本Dice值被区域大的Dice值掩盖,而分别计算后再平均能平等地考虑两者的Dice损失值,说明了分别计算Dice损失值是一种更为有效的方式。
在本研究的初期,我们发现坏死区域和非增强肿瘤区是以往单损失函数结构最难分割的区域,但这两个区域并不是脑胶质瘤的直接分割目标,这同样限制脑胶质瘤多区域分割精度的提升。为了直接有效地分割目标区域,我们引入多Dice损失函数。如表 2所示,对比原始的Dice损失函数,整个肿瘤区域的分割精度与后者几乎没差别。这可能是由于整个肿瘤区是所有除背景以外的组织区域合集,虽然单Dice结构需要同时学习各种组织之间的差异,但是背景的差异与肿瘤内组织的差异已经足够明显,所以多Dice损失函数并没有提升整个肿瘤的分割精度。增强肿瘤由于采用造影剂提升与其他组织的对比度,使得两者的差异相对明显,因而Dice系数提升较不显著。肿瘤核心区是由增强肿瘤、坏死组织和非增强肿瘤组成,相比整个肿瘤区的构成缺少水肿组织。水肿组织和肿瘤组织之间的边界往往较不清晰,导致单Dice损失函数较难同时学习好两者之间的差。我们提出的多Dice损失函数对于每一类区域都有一个分支进行针对性地特征提取,所以能显著地提升该区域的分割精度。Andrew[14]提出类似的想法,采用多个级联的三维U-Net分步预测脑胶质瘤各个区域的轮廓。为了将大区域的分割结果作为小区域的输入,该结构必须逐步训练,使得网络训练时间大幅增加。本网络结构同时输出多个区域的分割结果,有效减少网络的训练时间。
本文提出的改进能提升脑胶质瘤MRI的分割精度,可以归纳为如下3点原因:网络结构的目标函数与脑胶质瘤分割任务的目标具有更加直接的关联性,使得优化损失结构就能直接带来目标分割精度的提升;分割任务从原先的数个小区域转变为更大的区域,显著地降低了像素的类不平衡带来的缺点[23],更有利于网络参数的优化和分割精度的提升;原先的单损失函数由多分类函数转变为单分类函数,分割难度进一步下降[14]。
本研究还有一定的提升空间和不足:相比自然图像数据集(如ImageNet[24])该医学数据的样本量较小,尚未满足神经网络进行图像特征学习所需的样本数量;尚未引入Dropout[25]等其他优秀的网络结构,且本文的标签融合采用的是较为简单的求均值方式,还可以考虑设计更有效的加权求和或条件随机场[26]等图像后处理方式进行更好地预测。
综上所述,本研究结果显示,我们提出的基于三维全卷积DenseNet,使用多Dice损失函数进行脑肿瘤的分割任务的学习,并采用标签融合的方式进行后处理的神经网络结构是一种有效更为精确的脑胶质瘤MR图像分割方法。
| [1] |
万俊, 聂生东, 王远军. 基于MRI的脑肿瘤分割技术研究进展[J].
中国医学物理学杂志, 2013, 30(4): 4266-71.
|
| [2] |
Menze BH, Jakab A, Bauer S, et al. The multimodal brain tumor image segmentation benchmark (BRATS)[J].
IEEE Trans Med Imaging, 2015, 34(10): 1993-2024.
DOI: 10.1109/TMI.2014.2377694. |
| [3] |
Huang M, Yang W, Wu Y, et al. Brain tumor segmentation based on local Independent projection-based classification[J].
IEEE Trans Biomed Eng, 2014, 61(10): 2633-45.
DOI: 10.1109/TBME.2014.2325410. |
| [4] |
Prastawa M, Bullitt E, Ho S, et al. A brain tumor segmentation framework based on outlier detection[J].
Med Image Anal, 2004, 8(3): 275-83.
DOI: 10.1016/j.media.2004.06.007. |
| [5] |
Lefkovits L, Lefkovits S, Szilágyi L. Brain Tumor Segmentation with optimized random forest[C]//International Workshop on Brainlesion: Glioma, Multiple Sclerosis, Stroke and Traumatic Brain Injuries, 2016, 10670: 88-99.
|
| [6] |
Ying Z, Krauze AV, Ning H, et al. Brain tumor segmentation using holistically nested neural networks in MRI images[J].
Med Phys, 2017, 44(10): 5234-43.
DOI: 10.1002/mp.2017.44.issue-10. |
| [7] |
Havaei M, Davy A, Warde-Farley D, et al. Brain tumor segmentation with Deep Neural Networks[J].
Med Image Anal, 2017, 35: 18-31.
DOI: 10.1016/j.media.2016.05.004. |
| [8] |
Lopez MM, Ventura J. Dilated Convolutions for brain tumor segmentation in MRI scans[C]//International Workshop on Brainlesion: Glioma, Multiple Sclerosis, Stroke and Traumatic Brain Injuries, 2017, 10670: 253-62.
|
| [9] |
Kamnitsas K, Ledig C, Newcombe VFJ, et al. Efficient multi-scale 3D CNN with fully connected CRF for accurate brain lesion segmentation[J].
Med Image Anal, 2017, 36: 61-78.
DOI: 10.1016/j.media.2016.10.004. |
| [10] |
Jégou S, Drozdzal M, Vazquez D, et al. The one hundred layers tiramisu: Fully convolutional densenets for semantic segmentation [C]//Computer Vision and Pattern Recognition, 2017: 1175-83.
|
| [11] |
Fidon L, Li W, Garcia-Peraza-Herrera WC, et al. Generalised wasserstein dice score for imbalanced multi-class segmentation using holistic convolutional networks[C]//International Workshop on Brainlesion: Glioma, Multiple Sclerosis, Stroke and Traumatic Brain Injuries, 2017, 10670: 64-76.
|
| [12] |
Rahman MA, Wang Y. Optimizing intersection-over-union in deep neural networks for image segmentation[C]//International Symposium on Visual Computing, 2016: 234-44.
|
| [13] |
Milletari F, Navab N, Ahmadi S-A. V-net: Fully convolutional neural networks for volumetric medical image segmentation[C]// International Conference on 3D Vision, 2016: 565-71.
|
| [14] |
Beers A, Chang K, Brown J, et al. Sequential 3D U-Nets for biologically-informed brain tumor segmentation[OL]. [2017-12-15]. https://arxiv.org/pdf/1709.02967.pdf.
|
| [15] |
Sled JG, Zijdenbos AP, Evans AC. A nonparametric method for automatic correction of intensity nonuniformity in MRI data[J].
IEEE Trans Med Imaging, 1998, 17(1): 87-97.
DOI: 10.1109/42.668698. |
| [16] |
Huang G, Liu Z, Weinberger KQ, et al. Densely connected convolutional networks[C]//Computer Vision and Pattern Recognition, 2017: 4700-8.
|
| [17] |
Szegedy C, Liu W, Jia Y, et al. Going deeper with convolutions[C]// Computer Vision and Pattern Recognition, 2015: 1-9.
|
| [18] |
He KM, Zhang XY, Ren SQ, et al. Deep residual learning for image recognition[C]//2016 IEEE conference on computer vision and pattern recognition (CPVR), 2016: 770-8.
|
| [19] |
Ronneberger O, Fischer P, Brox T. U-Net: convolutional networks for biomedical image segmentation[C]//medical image computing and computer-assisted intervention, PT Ⅲ, 9351, 2015: 234-41.
|
| [20] |
Abadi M, Barham P, Chen J, et al. TensorFlow: A system for LargeScale machine learning[C]//USENIX Symposium on Operating Systems Design and Implementation, 16, 2016: 265-83.
|
| [21] |
Zhao X, Wu Y, Song G, et al. A deep learning model integrating FCNNs and CRFs for brain tumor segmentation[J].
Med Image Anal, 2018, 43: 98-111.
DOI: 10.1016/j.media.2017.10.002. |
| [22] |
Stawiaski J. A Multiscale Patch Based Convolutional Network for Brain Tumor Segmentation[OL]. [2017-12-15]. https: //arxiv. org/ pdf/1710. 02316. pdf.
|
| [23] |
Japkowicz N, Stephen S. The class imbalance problem: A systematic study[J].
Intelligent Data Analysis, 2002, 6(5): 429-49.
|
| [24] |
Russakovsky O, Deng J, Su H, et al. ImageNet large scale visual recognition challenge[J].
Int J Comput Vis, 2015, 115(3): 211-52.
DOI: 10.1007/s11263-015-0816-y. |
| [25] |
Srivastava N, Hinton G, Krizhevsky AA, et al. Dropout: a simple way to prevent neural networks from overfitting[J].
J Mach Learn Res, 2014, 15(1): 1929-58.
|
| [26] |
Krähenbühl P, Koltun V. Efficient inference in fully connected crfs with gaussian edge potentials[C]//Advances in Neural Information Processing Systems, 2011: 109-17.
|
 2018, Vol. 38
2018, Vol. 38

