在医学研究中，经常需要对不同测量者或测量方法进行一致性评价，其中对于二分类变量，最早由Scott在1955年提出了π系数，如今应用最广泛的是kappa系数^[1-3]，之后，Fleiss和Conger把kappa拓展到多个评价者中，但是依然存在kappa悖论问题。在2008年，Gwet提出了一个更稳健的一致性评价系数AC₁^[4-5]，其不受评价者边缘概率分布的影响，但是有研究者提出其方差估计方法有一定的缺陷^[6]。近期，又有学者Locatelli^[7]提出了以“intra-class odds ratio”的概念来评价一致性，但是其分布范围在0到无穷大，不易量化评价一致性结果。为了克服kappa悖论，以及实现更高准确性和稳定性的一致性评价，本文针对二分类变量提出了一种新的基于AC₁系数的一致性评价方法CEA（coefficient of evaluation agreement），该方法在AC₁系数的理论基础上推导出不同测量者（或不同测量方法）阳性事件率之间的关系来估计阳性事件率及偶然一致性，并通过探究阳性事件率和偶然一致性对整体一致性的影响，利用各个概率之间的关系式及取值范围来估计整体一致性。为验证CEA系数的准确性与稳定性，本文对kappa、AC₁、CEA系数进行了模拟比较。

1 材料和方法 1.1 Kappa系数

Kappa系数^[10-13]是目前使用最广泛的一致性评价指标，一般适用于二分类以及多分类结局变量，加权kappa适用于有序变量，其公式组成部分主要由观测一致性和偶然一致性两部分组成。假定有A和B两个评价者将样本量为n的同一份样本分为1和0两类，结果可以通过以下2×2四格表给出，其中n_ij表示评价者A和B把研究对象分别分到类别i和类别j的个数，n₁₊，n₀₊和n₊₁，n₊₀分别代表评价者A和B把总样本分到类别1和0的总数。

Cohen所提出的针对二分类和多分类kappa计算公式为：

$ \kappa = \frac{{{p_o} - {p_{c\left| \kappa \right.}}}}{{1 - {p_{c\left| \kappa \right.}}}} $

(1)

此处，${p_o} = \frac{{{n_{11}} + {n_{00}}}}{n}$代表A和B的观测一致性，${p_{c|\kappa }} = (\frac{{{n_{1 + }}}}{n} \times \frac{{{n_{ + 1}}}}{n}){\rm{ }} + (\frac{{{n_{0 + }}}}{n} \times \frac{{{n_{ + 0}}}}{n})$代表偶然一致性。

然而，Feinstein和Cicchetti发现kappa系数有两个悖论^[14-15]，第一，kappa的大小受阳性一致率与阴性一致率差值的影响，因此会出现与观测一致性相差较大的情况；第二，kappa系数会受评价结果边缘分布的影响：在其他条件不变的条件下，相比于边缘分布均衡，其分布不均衡时的kappa值会偏大。

1.2 AC₁系数

AC₁首先由Gwet提出^{[4, 16-17]}，其给予一致性评价一种全新的解释：首先，将评价结果分为确定评价和随机评价两个部分，假定评价者做出随机评价的概率为r_i（i为评价者A或评价者B），当评价者做出随机评价时，其将会有0.5的概率做出正确的判断；其次，假定当两个评价者做出确定的评价时，结果完全一致。因此，AC₁有两个使用前提：第一，当评价者做出随机判断即认为出现偶然一致性；第二，当评价对象有部分不确定时即做出随机评价。相应的结果如表 2所示。

AC₁的计算方法见式（2）：

$ A{C_1} = \frac{{{p_o} - {p_{c\left| {A{C_1}} \right.}}}}{{1 - {p_{c\left| {A{C_1}} \right.}}}} $

(2)

其中

$ \begin{array}{l} {p_o} = \frac{{{n_{11}} + {n_{00}}}}{n} = \\ \frac{{{n_{11RR}} + {n_{00RR}} + {n_{11CR}} + {n_{00CR}} + {n_{11RC}} + {n_{00RC}} + {n_{11CC}} + {n_{00CC}}}}{n} \end{array} $

可见，AC₁的公式形式类似于kappa系数，不同在于偶然一致性p_c|AC1的计算：AC₁系数假定p_c|AC1需要同时服从上述假定。因为在实际情况中p_c|AC1不能够得到，AC₁方法用以下公式来估计p_c|AC1 :

$ {p_{c\left| {A{C_1}} \right.}} = 2q\left( {1 - q} \right) $

(3)

其中$q = ({n_{1 + }} + {n_{ + 1}})/2n$。

以下将介绍本文提出的一种新的基于AC₁系数的一致性评价方法CEA。

1.3 一致性估计系数CEA

除了前述AC₁系数，还有Scott's π、G-index等，这些一致性系数的不同主要体现在偶然一致性p_c的构建。由于不同的p_c估计方法会影响到其自身的估计误差，进而会影响到最终结果的准确性。本文在AC₁的基础上提出了一种新的一致性评价方法CEA。首先，为了对比多种一致性系数先来定义一下金标准T。金标准的计算公式结构采用kappa家族的公式结构，通过观测一致性p_o和偶然一致性p_c获得（式4）：

$ T = \frac{{{p_o} - {p_c}}}{{1 - {p_c}}} $

(4)

式中，${P_c} = ({n_{11RR}} + {n_{00RR}} + {n_{11RC}} + {n_{00RC}} + {n_{11CR}} + {n_{00CR}})/n$。在现实工作中，T不能通过2×2四格表得到，但是模拟时可通过所设置参数获得。

和Kappa系数的公式结构类似，本研究所提出的CEA系数校正了其中的偶然一致性。假定有两个评价者A和B对同一个样本进行评判，二分类评判结果用0和1表示，评价者A有r_a的概率做出随机评判，评价者B有r_b的概率做出随机评判，当任意一个评价者做出随机评判时，他们将以0.5的概率做出正确的评判。并且假定当两个评价者都做出确定的评判时，评价结果完全相同。评价者A和评价者B把所有研究对象分到类别1中的概率分别为p_a和p_b，即表 1中p_a = n₁₊/n，p_b = n₊₁/n，评价者A和评价者B同时把同一个测评对象分到同一个类别的概率为p_o，即表 1中p_o =(n₁₁ + n₀₀)/n，代表总观测一致性，样本的阳性事件率为p_r。因为当评价者A和B做出随机评判时，他们都将以0.5的概率做出正确的判断，那么可以根据以下公式^[4]估计偶然一致性${{\hat p}_c}$：

$ {{\hat p}_c} = \frac{1}{2}\left( {{{\hat r}_a} + {{\hat r}_b} - {{\hat r}_a}{{\hat r}_b}} \right) $

(5)

其中，${{\hat r}_a}$和${{\hat r}_b}$分别为评价者A和B做出随机评判概率的估计值，那么为了估计r_a和r_b, 可推导出p_a、p_b、p_r和p_o之间的关系为：

$ {p_a} = {p_r} - \frac{1}{2}{p_r}{r_a} $

(6)

$ {p_b} = {p_r} - \frac{1}{2}{p_r}{r_b} $

(7)

$ {p_o} = 1 - \frac{1}{2}\left( {{r_a} + {r_b}} \right) + \frac{1}{2}{r_a}{r_b} $

(8)

由上述公式计算可得：

$ f\left( {{p_r}} \right) = \left( {{p_o} - 1} \right)p_r^2 + \left( {{p_a} + {p_b}} \right){p_r} - 2{p_a}{p_b} $

(9)

其中p_a、p_b和p_o可直接由原始数据获得，则最终可通过解一元二次方程f(p_r) = 0来估计p_r，根据定义可知p_r取值范围为0~1，当一元二次方程在取值范围内有两个解，则取更靠近p_a及p_b均值的值作为p_r；当一元二次方程在在取值范围内有且只有一个解，则取唯一解作为p_r；当一元二次方程无解时，因p_o的取值范围为0~1，取一元二次方程f(p_r)最大值作为p_r。那么，最终CEA的计算公式如下：

$ CEA = \frac{{{p_o} - {{\hat p}_c}}}{{1 - {{\hat p}_c}}} $

(10)

这里${{\hat p}_c}$由式5获得。相关的计算与结果可以通过R软件实现。

1.4 模拟部分

为比较本研究所提出的一致性评价方法CEA的准确性，本文对kappa、AC₁、CEA及其方差在多种情况下做了蒙特卡罗模拟。首先，模拟一组样本量为N并由0~1为元素的二分类变量，其阳性事件率为p_r；其次分别以r_a和r_b的概率从中抽取部分数据，再将这部分数据以0.5的概率赋值0或者1；最后将新赋值后的这部分数据放回原数据中，此过程将产生两组数据，分别代表两个评价者A和B的评判结果。真实的一致性T将由公式（4）计算得出，kappa、AC₁和CEA将由评价者A和B的评判结果组成的2×2四格表计算得出。之后，本文对各个一致性系数的方差也做了模拟，参数设置如下：样本量N=20、60、80、100，样本的阳性事件率p_r =0.95、0.85、0.75、0.55，评价者A和B发生随机评判的概率r_i =0.05、0.2；各种情形下均模拟10 000次。

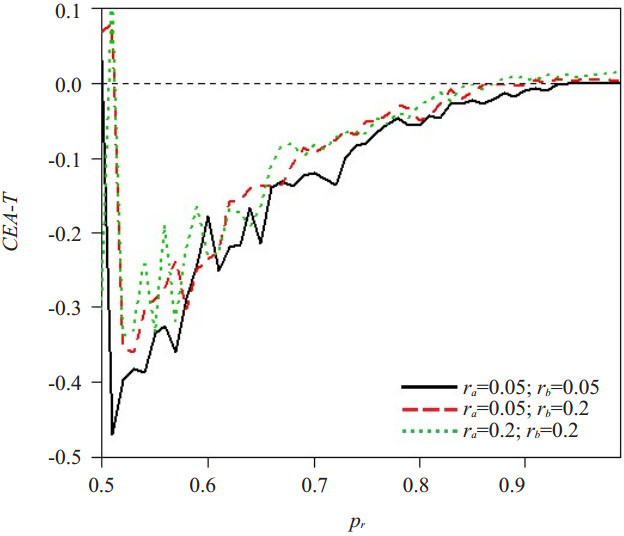
2 结果 2.1 模拟结果

随着阳性事件率p_r的增长，CEA对真实一致性T的估计偏差逐渐减小，图 1展示了两个评价者的随机评判概率为0.05、0.2不同组合下的结果。鉴于不同的p_r条件下，图 1是以0.5为中心左右对称的，此处只展示了p_r在0.5~1范围内CEA的估计偏差。

当p_r =0.95时，金标准T和kappa、AC₁、CEA的偏差见表 3。系数偏差$Bias = \frac{1}{{10000}}\sum\limits_{s = 1}^{10000} {({{\hat T}_s} - T) \times 100\% } $，${{{\hat T}_s}}$代表在样本量为N的10000次模拟中，各个方法每次的估计值。可见当r_i =0.05、0.2时，CEA系数偏差的分布范围从-1.05%到1.07，始终小于或者等于另外两个指标。同样，对于p_r =0.85，p_r =0.75和p_r =0.55的情况也进行了模拟，结果与表 3类似：当p_r =0.85，r_i =0.05、0.2时，CEA系数偏差的分布范围从-4.18%到-3.41%，AC₁系数偏差的分布范围从-7.23%到-6.51%；当p_r =0.75，r_i=0.05、0.2时，CEA系数偏差的分布范围从-9.20%到-9.06%，AC₁系数偏差的分布范围从-17.21%到-13.9%；当p_r =0.55，r_i =0.05、0.2时，CEA系数偏差的分布范围从-20.30%到-7.05%，AC₁系数偏差的分布范围从-41.32%到-30.01%。即在不同的条件下，CEA的偏差始终最小。

样本量和阳性事件率p_r对各个系数方差的影响结果见表 4。

方差$V = \frac{1}{{10000}}\sum\limits_{s = 1}^{10000} {{{({{\hat T}_s} - average({{\hat T}_s}))}^2} \times 100\% } $，${{{\hat T}_s}}$代表在样本量为N的10 000次模拟中，各个方法每次的估计值，${\bar T}$代表金标准10 000次模拟的均数。可见随着阳性事件率p_r的增长，kappa估计值的方差单调递增，而AC₁和CEA估计值的方差呈减少趋势；在相同的阳性事件率p_r下，随着样本量N的增加，所有一致性系数估计值的方差都在减少；虽然p_r等于0.55，0.75和0.85时，kappa系数部分估计值的方差是最小的，但是其系数估计值偏差始终最大；CEA估计值的方差始终小于AC₁的方差。

2.2 实例分析

此实例描述了描述了巴塞罗那及西班牙的72岁以上老年人步行和从椅子上站起来的困难程度，并进行了基本的测量（步行速度和chair-stand测试）^[18]。并进行了基本的测量（步行速度和chair-stand测试）。表 5显示了对是否在行走时需要帮助和是否可以完成4米步行的基本测量结果和自评结果的比较。

这是一个关于kappa悖论典型的例子，根据公式（1）、（2）、（9）可以得出kappa、AC₁、CEA的估计值分别为0.519、0.920、0.961，从表格给出的结果可以看出观测一致性很高（p_o = 0.962），但是kappa系数却显示出很低的一致性，而CEA与AC₁的结果类似，并且都不受边缘概率分布的影响。

3 讨论

近些年，在医学领域评价不同方法或者不同评价者之间的一致性受到了极大的关注^[19-21]。然而，这些方法都有他们各自的限制条件，最典型的就是kappa悖论，为克服该缺陷，并提高准确性，本研究提出了一种新的针对二分类变量的一致性评价方法CEA。类似于kappa^{[1, 22-25]}和AC₁系数的公式结构，CEA对偶然一致性进行了校正，为了估计最接近真实值的偶然一致性，本研究探索了两个评价者做出随机评价概率r_a、r_b与阳性事件发生率p_r之间的关系，并通过解一元二次方程及概率本身的取值范围来确定最终的估计值。与AC₁类似，CEA也有如下假设前提：（1）评价者A和B都会有一定的概率做出随机评判，并且当他们做出随机评判时，他们将以0.5的概率做出正确的判断。（2）当两个评价者对同一个测评对象做出确定评判时，两者的评判结果将完全一致。

为了评估CEA的可靠性，本研究对kappa、AC₁和CEA进行了模拟研究。结果显示，在我们所设置的不同的样本量（20、60、80或100）、阳性事件率（0.95、0.85、0.75或0.55）以及随机评判概率（0.05或0.2）条件下，CEA和金标准的偏差始终最小，说明CEA的准确性高于kappa和AC₁；随着p_r的减小，CEA的准确性增高，即使阳性事件率接近于极值的情况下，CEA仍没有受到边缘概率分布的影响且始终保持高度的准确性；在方差模拟结果中，在我们所设置的不同的样本量（同上）、阳性事件率（同上）以及随机评判概率（r_a = r_b =0.05）条件下，CEA估计值的方差小于AC₁估计值的方差，虽然当p_r =0.55、0.75、0.85时，kappa估计值的方差部分小于AC₁和CEA估计值的方差，但是kappa估计值的方差和CEA估计值的方差差别并不大，并且CEA解决了kappa悖论的问题，即使在小样本的情况下依旧表现良好。因此，无论是在准确性还是稳定性的方面考虑，CEA都是一个值得推荐的一致性评价方法。

但CEA也有不足之处，由图 1可知，当阳性事件率p_r在0.5~0.6时，CEA与真实一致性T的差值波动较大，但是其准确性仍高于kappa和AC₁。此外，模拟中发现虽然评价者的随机评判概率的估计误差较大，但由于偶然一致性的计算结合了两个随机评判概率的乘积与加和，最终对偶然一致性的估计误差影响较小，使得CEA准确性仍高于kappa和AC₁。上述问题有待于进一步研究。