2. 南方医科大学 南方医院普外科//广东省微创外科工程中心,广东 广州 510515
2. Department of General Surgery, Nanfang Hospital, Guangdong Provincial Engineering Technology Research Center of Minimally Invasive Surgery, Southern Medical University, Guangzhou 510515, China
胃肠道间质瘤(GIST)是胃肠道最常见的间叶源性肿瘤,独立起源于胃肠道壁、具有非定向分化特征,可发生于消化道任何部位,胃是最好发部位[1-2]。GIST的常见临床表现复杂,缺乏特异性,且小间质瘤往往无明显临床症状,对于其术前诊断较为困难。所有的GIST都具有一定的恶性潜能,早期可出现肝脏和腹腔转移。因此GIST的良恶性是临床最为关注的问题,它直接决定着临床治疗方案的制定和患者的预后。
临床上,非侵入的医学成像技术对胃部恶性肿瘤的诊断和风险分级具有重要的作用[3]。计算机断层扫描(CT)是检查胃部肿瘤以及评价肿瘤恶性程度最常用的技术,其扫描结果有助于预测胃肠道间质瘤的恶性潜能及预后[4]。随着多层螺旋CT空间分辨率和密度分辨率的不断提高,CT已经成为胃部肿瘤术前诊断及分期必不可少的检查手段之一[5]。虽然CT对肿瘤的检出、判断肿瘤与周围器官的关系及有无转移有重要价值[6],但在判断肿瘤的良恶性方面仍有困难[7]。由于GIST的CT表现与其病理组织学相关,仍有不少患者是经手术切除或者探查取得标本进行病理、免疫组化检查后,才能明确诊断。
放射组学通过提取高通量的图像特征能够将影像数据转化为高维可发掘的特征空间数据,其核心假设是对图像特征数据进行自动化分析获取对疾病的诊断、预后及预测有价值的信息[8]。放射组学的一般流程为:获取高质量、标准化的图像,并通过自动化分割算法[9]或临床专家勾画确定肿瘤区域;从肿瘤区域提取大量的图像特征(200+),如灰度分布、灰度级之间的空间关系、纹理异质性等;对于大量冗余的特征进行选择,选取对预测结果最有效且使得预测模型简洁的特征;通过对选定的特征与结果进行分析建立预测模型[10]。大量研究表明放射组学的研究方法能够从图像中获取更多有用的信息并且在提高诊断和预后价值方面具有极大的潜能[11-14]。目前应用放射组学方法研究胃部肿瘤的研究相对较少。Ba-Ssalamah等[15]应用纹理分析对胃腺癌、淋巴瘤和GIST进行分类。Ma等[16]从CT图像中提取485个特征并通过LASSO算法选择其中2个特征构建模型区分Ⅳ型胃癌与原发性胃淋巴瘤,得到的准确率、AUC、敏感性及特异性分别为0.84、0.89、0.87、0.83。
本文以GIST为研究对象,通过放射组学分析首次建立了一个对其进行良恶性分类的模型。我们首先从动脉期的CT图像中为每个病人提取了9690维纹理特征;然后应用0.632+bootstrap [17]对初始特征集进行特征降维,得到包含25个特征的特征子集;再次应用0.632+ bootstrap在特征子集中进行特征选择,得到了6个特征的最佳组合;最后通过逻辑回归求解系数得到最终的多变量模型。1000个bootstrap样本在训练集和验证集中均得到了良好的分类结果。
1 资料和方法 1.1 实验数据本研究回顾性地分析了2008年1月~2015年12月在南方医院确诊的110个GIST病例。其中男性63例,女性47例;平均年龄57,年龄范围34~72;胃部为原发病灶的有84例,其他部位的有26例;肿瘤最大径为2.2~ 11.8。依据NIH2008标准[18],将病人分为4种不同风险程度:极低危11例,低危45例,中危25例,高危29例。为了对GIST良恶性进行二分类,我们将极低危和低危GIST标记为良性(共56例,男性34例,女性22例),中危和高危GIST标记为恶性(共54例,男性31例,女性23例)。病例的纳入标准为:经手术切除肿瘤;确诊时未出现转移;肿瘤未破裂;至少术前15 d采集动态增强CT图像;具有完整的临床病理数据。
CT扫描采用GE LightSpeed16(n=32)和GE LightSpeed VCT(n=78)扫描仪。扫描协议为:管电压120 kV,管电流130 mA,旋转时间0.5 s,准直器宽8 mm× 0.625 mm和64 mm×0.625 mm,视野大小为350 mm× 350 mm,图像分辨率为512×512,层厚为5 mm,螺距0.6。在获取常规平扫CT图像之后,以3.5 mL/s的速率打入1.5 mL/kg的Ultravist非等离子造影剂,25~30、60、180 s之后分别做动脉期、门静脉期、平衡期扫描。CT图像应用软组织算法(B30f)重建。
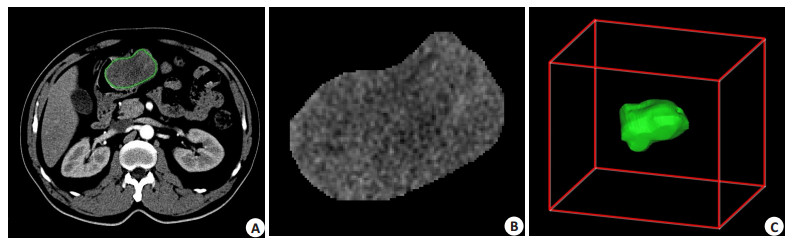
1.2 特征提取在提取特征之前首先由影像专家应用ITK-SNAP和Mimics软件把每一个病人图像中GIST部位逐层勾画,然后分割出来生成三维的感兴趣容积(VOI)。如图 1所示,(A)为GIST二维的CT动脉期图像,绿色曲线为专家勾画的边界,(B)为二维分割结果,(C)为三维重建得到的VOI。
|
图 1 图像预处理 Figure 1 Image preprocessing. A: GIST delineated by expert; B: Segmentation result; C: Reconstruction result of VOI. |
我们为每一个病人在其VOI中提取了5大类43种纹理特征:一阶统计特征3个、灰度共生矩阵[19](GLCM)特征9个、灰度游程矩阵[20](GLRLM)特征13个、灰度区域尺寸矩阵[21](GLSZM)特征13个、邻域灰度差分矩阵[22](NGTDM)特征5个。提取过程以及后续的统计分析都是应用Vallieres等[23]编写的RADIOMICS工具包在MATLAB上进行操作的。
纹理特征提取过程要经历3个步骤,其中包含了4个提取参数:
(1)小波带通滤波。通过在小波域中为带通子带赋予不同的权重,能够增强或减弱高频信息,从而获得具有不同特性的纹理特征[24]。将VOI转换到小波域后,低通(LLL)和高通(HHH)子带保持不变,赋予其他子带(LHL,LHH,LLH,HLL,HHL,HLH)不同的权重。将权重的比值定义为ω,本文中应用的比值为[1/2, 2/3, 1, 3/2, 2]。
(2)各向同性重采样。在计算纹理特征之前,需要对VOI用立方插值进行重采样得到合适的分辨率。例如VOI中原始的体素大小为3.2 mm×3.2 mm×1.7 mm,设定各向同性的尺寸为3 mm,则经过重采样之后体素大小变为3 mm×3 mm×3 mm。图像重采样中的插值操作,通常会引起图像的某些统计特性发生变化,因此通过不同尺寸的各向同性重采样能够获得更多的纹理信息。本文中将重采样尺寸定义为S,取值为1、2、3、4、5 mm以及图像原始的分辨率。
(3)灰阶离散化。计算高阶的纹理特征之前,VOI的整个灰度范围需要映射到不同数量的灰度级。量化算法(Q.A)和灰度级数量(Ng)是量化过程中用到的两个参数。本文中用到的量化算法是Equal-probability和Lloyd-Max [25],灰度级数量是[8,16,32,64]。
一阶统计特征的提取过程中仅仅应用到ω和S两个参数,提取了3×5×6=90个特征;高阶的纹理特征(GLCM、GLRLM、GLSZM、NGTDM)的提取过程中用到了4个参数,提取了(9+13+13+5)×5×6×2×4=9600个特征。因此,我们最终为每个病人提取了9690个纹理特征。
1.3 建立预测模型本文将110个病人随机划分80个作为训练集,30个作为独立的验证集。在训练集中用逻辑回归建立一个包含p个特征的分类模型:
| $ R(x) = {\beta _0} + {\beta _1}{x_1} + {\beta _2}{x_2} + \cdots {\beta _p}{x_p} $ | (1) |
其中x ={xi, i = 1, 2, …, p}表示选择的特征,β ={βi, i = 0, 1, …, p}表示回归系数。给定一个新的病例时,预测模型的输出应该使得将其判定为0或者1的概率最大。于是,我们用如下形式的Logit变换将R(x)转换为恶性的概率(0~1):
| $ \pi (x) = P(y = 1|x) = \frac{{e^{R(x)}}}{{1 + {e^{R(x)}}}} $ | (2) |
将训练集记为X,应用bootstrap对其采样1000次,得到的样本集记为X*,未出现在X*中的数据集记为X†。训练过程中用AUC0.632+评估模型的分类性能[23]:
| $ \begin{array}{l} {[{\rm{AUG}}]_{{{0.632}_{\rm{ + }}}}} = \frac{1}{N}\sum\limits_{n = 1}^N {[(1-\alpha (n)) \cdot {\rm{AUC}}(\boldsymbol{{\rm{X}, {\rm{X}}}}) + \alpha (n) \cdot \max \{ 0.5, {\rm{AUC(}}{\boldsymbol{{\rm{X}}}^{\rm{*}}}{\rm{, }}{\boldsymbol{{\rm{X}}}^\dagger }{\rm{)}}\}]} \\ {\rm{where}}\;\;\;\;\;\;\;\;\;\alpha (n) = \frac{{0.632}}{{1 -0.368 \cdot R(n)}}\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;R(n) = \left\{ \begin{array}{l} 1\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;if\;\;{\rm{AUC}}({\boldsymbol{{\rm{X}}}^{\rm{*}}}{\rm{, }}{\boldsymbol{{\rm{X}}}^\dagger }) \le 0.5\\ \frac{{{\rm{AUC}}(\boldsymbol{{\rm{X}, {\rm{X}}}}) -{\rm{AUC}}({\boldsymbol{{\rm{X}}}^{\rm{*}}}{\rm{, }}{\boldsymbol{{\rm{X}}}^\dagger })}}{{{\rm{AUC}}(\boldsymbol{{\rm{X}, {\rm{X}}}})}}\;\;\;if\;\;1 < \frac{{{\rm{AUC}}(\boldsymbol{{\rm{X}, {\rm{X}}}})}}{{{\rm{AUC}}({\boldsymbol{{\rm{X}}}^{\rm{*}}}{\rm{, }}{\boldsymbol{{\rm{X}}}^\dagger })}} < 2\\ 0\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;otherwise \end{array} \right. \end{array} $ | (3) |
其中AUC(X, X)表示在X中训练得到分类器,然后在X中测试得到的AUC值;AUC(X*, X†)表示在X*中训练得到分类器,并且在X†中测试得到的AUC值。
1.3.1 特征降维训练集中每个病人有9690个特征,存在大量冗余。如果将所提取的特征全部用于建立分类模型,必然会降低模型的预测效果且增加了计算时间,因此在特征选择之前需要对其进行降维。公式4用逐步前向选择算法在初始特征集中选择一个包含25个特征的特征子集。
| $ \begin{array}{*{20}{l}} {\mathop {\arg \;\max }\limits_j \;\;\frac{1}{2}|r({x_j},y)| + }\\ {\frac{1}{2}\left[ {\sum\limits_{k = 1}^f {\left( {\frac{{2(f - k + 1)}}{{f(f + 1)}}} \right) \cdot (1 - MIC({x_k},{x_j}))} } \right]} \end{array} $ | (4) |
公式中第1项表示候选特征与类别之间的相关性,其中r(xj, y)为特征xj与类别y的相关系数;第2项表示候选特征与已选特征之间的不相关性,其中f为当前已选入特征子集中的特征个数;MIC(xk, xj)为特征xj与xk之间的最大信息系数[26-27],计算公式为:
| $ MIC({x_k}, {x_j}) = \mathop {max}\limits_{a*b < B} \frac{{MI({x_k}, {x_j})}}{{{\rm{log}}({\rm{min}}\{ a, b\} )}} $ | (5) |
其中MI(xk, xj)表示xj与xk的互信息,a, b为xj与xk的散点图在两个方向上划分网格的数目,B取值为数据量的0.6次方。
对X*中的1000个样本,(1)计算初始特征集中所有特征与类别之间的相关系数并求其均值,选择其中最大的一个作为特征子集中的第一个特征;(2)逐步在剩余特征中通过求解公式4添加特征,直到特征子集中包含25个特征为止。
1.3.2 特征选择对于特征子集中的25个特征,分别进行25次实验得到包含1~10个特征的250个候选模型。(1)取其中1个特征作为该模型的第1个特征(启动子),在X*中进行逻辑回归得到模型并通过X†计算该模型的AUC0.632+、敏感性、特异性。计算敏感性及特异性的公式为[23]:
| $ \begin{array}{l} {[{\rm{S}}]_{{{0.632}_{\rm{ + }}}}} = \frac{1}{N}\sum\limits_{n = 1}^N {[(1-\alpha (n)) \cdot {\rm{S}}(\boldsymbol{{\rm{X}, {\rm{X}}}}) + \alpha (n) \cdot {\rm{S(}}{\boldsymbol{{\rm{X}}}^{\rm{*}}}{\rm{, }}{\boldsymbol{{\rm{X}}}^\dagger }{\rm{)}}]} \\ {\rm{where}}\;\;\;\;\;\;\;\;\;\alpha (n) = \frac{{0.632}}{{1 -0.368 \cdot R(n)}}\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;R(n) = \left\{ \begin{array}{l} \frac{{{\rm{S}}(\boldsymbol{{\rm{X}, {\rm{X}}}}) -{\rm{S}}({\boldsymbol{{\rm{X}}}^{\rm{*}}}{\rm{, }}{\boldsymbol{{\rm{X}}}^\dagger })}}{{{\rm{S}}(\boldsymbol{{\rm{X}, {\rm{X}}}})}}\;\;\;\;if\;\;\frac{{{\rm{S}}(\boldsymbol{{\rm{X}, {\rm{X}}}})}}{{{\rm{S}}({\boldsymbol{{\rm{X}}}^{\rm{*}}}{\rm{, }}{\boldsymbol{{\rm{X}}}^\dagger })}} > 1\\ 0\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;otherwise \end{array} \right. \end{array} $ | (6) |
其中[S]0.632+表示敏感性或特异性;S(X, X)表示在X中训练得到分类器,然后在X中测试得到的敏感性或特异性值;S(X*, X†)表示在X*中训练得到分类器,并且在X†中测试得到的敏感性或特异性值。
(2)逐步前向增加模型的阶数。对于剩下的24个特征,逐个与启动子合并。在X*中进行逻辑回归得到模型并通过X†计算该模型的AUC0.632+。选择使得AUC0.632+最大的特征加入模型。以此类推,直到模型的阶数为10。
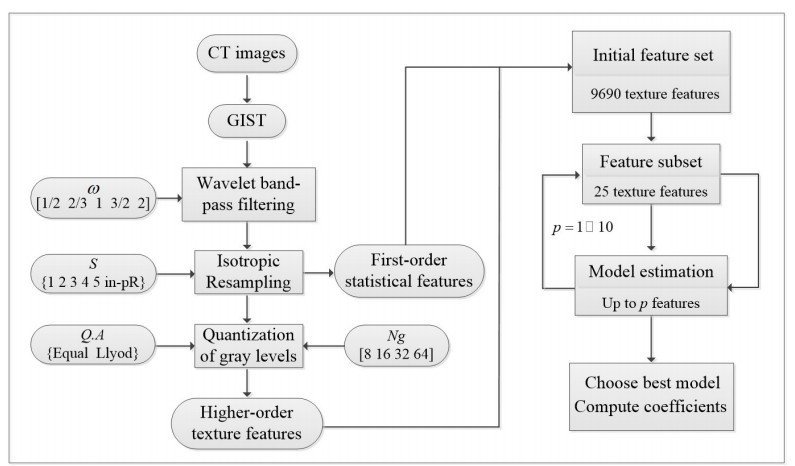
1.3.3 求解模型(1)固定模型的阶数,从25次实验中选择使得AUC0.632+最大的一个模型,得到具有1~10个特征的10个候选模型。(2)计算10个候选模型的AUC0.632+、敏感性、特异性,选择最佳的特征组合构建分类预测模型。(3)在X*中进行逻辑回归得到回归系数并取其均值,最终得到包含p个特征的分类模型。本文方法的流程如图 2所示。
|
图 2 方法流程图 Figure 2 Illustration of the proposed method. |
表 1所示为通过降维得到的特征子集及每个特征与类别之间的相关系数,其中包括8个GLCM特征、8个GLRLM特征,7个GLSZM特征,2个NGTDM特征。为了检验这些特征与类别之间相关性是否显著,应用多重检验中Bonferroni校正方法对显著性水平进行校正。这里我们设置α = 0.05,多重检验次数K取特征子集的特征个数,因此认为p < α/K = 0.05/25 = 0.002的特征与类别之间是显著相关的(表 1中粗体字所示)。
| 表 1 特征子集中25特征的提取参数与相关性检验 Table 1 Extraction parameters and correlation test of 25 features in the feature subset |
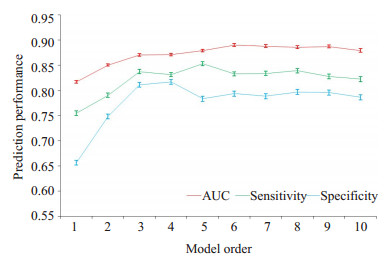
图 3所示为10个候选模型的预测表现估计及其95%置信区间。由图可知,模型阶数低于5时,预测表现与模型阶数成正比;模型阶数在6~8时预测表现最优且稳定;模型阶数大于8时预测表现开始下降。出于模型简洁性的考虑,我们最终选择6个特征组合构建最终的预测模型。该组合下1000个bootstrap样本得到的AUC、敏感性、特异性、准确率及其95%的置信区间分别为:0.8905 ± 0.0028,0.8330 ± 0.0041,0.7936 ± 0.0051,0.8112±0.0028。
|
图 3 候选模型的预测表现估计 Figure 3 Prediction performance estimation of the candidate models. |
应用逻辑回归求解模型的回归系数,建立的GIST良恶性分类预测模型为:
| $ \begin{array}{l} R(\boldsymbol{x}) = 69.7-2871 \times {\rm{GLSZM}}-{\rm{ZSV}}(\omega = 2, S = 5, Q.A = Equal, Ng = 16)\\ \;\;\;\;\;\;\; + 24.97 \times {\rm{GLSZM}}-{\rm{SZM}}(\omega = 0.67, {\rm{S}} = 4, Q.A = Equal, Ng = 8)\\ \;\;\;\;\;\;\; - 0.2381 \times {\rm{NGTDM}} - {\rm{Strength}}(\omega = 0.67, S = 4, Q.A = Equal, Ng = 64)\\ \;\;\;\;\;\;\; - 8.466 \times {\rm{GLCM}} - {\rm{Entropy}}(\omega = 0.67, S = 5, Q.A = Equal, Ng = 64)\\ \;\;\;\;\;\;\;{\rm{ + }}0.0143 \times {\rm{GLRLM}} - {\rm{HGRE}}(\omega = 0.67, S = 5, Q.A = Equal, Ng = 64)\\ \;\;\;\;\;\;\; - 0.0694 \times {\rm{GLCM}} - {\rm{Contrast}}(\omega = 2, S = 5, Q.A = Llyod, Ng = 32) \end{array} $ | (7) |
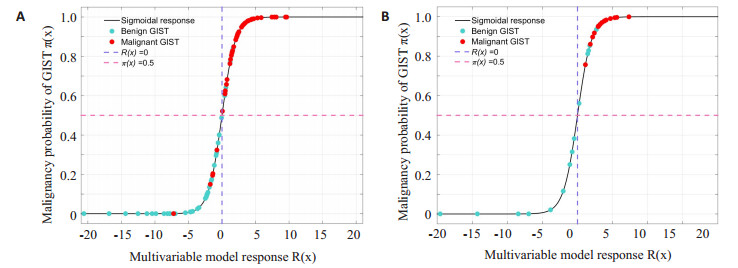
图 4(A)、(B)分别显示了分类预测模型在训练集和验证集中的分类结果。由图 4可知,训练集和验证集中良性GIST的预测模型响应R(x)基本位于R(x) < 0的区域,其均值分别为-3.55和-4.44;恶性GIST的预测模型响应R(x)基本位于R(x)>0的区域,其均值分别为3.17和2.61。应用t检验对训练集和验证集中良恶性GIST的预测模型响应R(x)进行显著性检验得到的p值均远远小于0.0001,因此可以将R(x)=0作为阈值对GIST的良恶性进行有效的分类。应用Logit变换将R(x)变换为概率之后,良性GIST的π(x)基本位于π(x) < 0.5的区域,而恶性GIST的π(x)基本位于π(x)>0.5的区域。因此也可以将π(x)=0.5作为阈值对GIST的良恶性进行有效的分类,两种阈值得到的分类结果相同。
|
图 4 GIST分类结果(A)训练集(B)验证集 Figure 4 Classification results of GIST in the training cohort (A) and validation cohort (B). |
本文分别在训练集和验证集中用1000个bootstrap样本对分类模型进行了验证。训练集中GIST良恶性分类得到的AUC、敏感性、特异性、准确率及其95%的置信区间分别为:0.9337±0.0010,0.8846±0.0019,0.8467± 0.0021,0.8658±0.0014。验证集中得到的AUC、敏感性、特异性、准确率及其95%的置信区间分别为0.9065± 0.0028、0.8658±0.0037、0.8600±0.0039、0.8632±0.0025。
3 讨论本文以放射组学的方法研究胃肠道间质瘤,提出一个基于CT图像的GIST良恶性分类模型,实验结果证明该模型具有良好的分类性能。作为一种无创的预测方法,该模型能够为术前治疗方案的制定和病人预后提供参考信息。
目前,确认肿瘤的VOI并从其中提取特征是放射肿瘤学的核心[28]。本文中由VOI特征建立模型对GIST的良恶性进行精确分类是可重复的操作。作为一种计算机辅助诊断技术,放射组学分析有助于经验较少的放射医师且由于其采用自动化算法减少了观察者之间的差异。另外,放射组学分析是对现有图像进行操作而不需要另外的代价。
本文得到高精度分类结果主要有3个原因。其一,特征过程提取中通过提取参数的设定使图像信息更加丰富,得到了大量的纹理特征。研究表明不同的提取参数会影响纹理特征值,进而影响分类结果,且应用所有参数时能够获得更好的分类结果[23]。如表2所示,参数S一列中5 mm超过一半且未选取到图像本身的分辨率,说明这一参数对分类结果的影响最大,这与Vallieres等[23]的研究结论是一致的。其二,由于VOI包含了所有2D层面,因此3D特征包含了更丰富的信息[29]。其三,我们从动脉期CT图像中提取特征。相比非增强的图像,动脉期图像显示了肿瘤的更多细节且增强了肿瘤异质性[30]。在构建模型的过程中未考虑临床上常用的最大径是因为纹理特征包含了更多的肿瘤异质性的信息[31]。
本文仍然存在几个局限性。首先,通过提取参数的设定得到了大量的纹理特征,这对分类结果的影响是正面的。但是也使得特征降维过程耗时较长,因此设计运行速度快且鲁棒性强的算法是未来需要探讨的工作,也是放射组分析标准化中需要解决的问题。其次,我们将极低危和低危划分为良性,中危和高危划分为恶性,只针对GIST做了二分类,未来将致力于对GIST做精确的四分类。最后,验证集与训练集采自同一个数据中心,通过搜集其他中心的数据可以更加有效地验证本文方法的鲁棒性。同时,将本文方法应用到更多的疾病也是未来即将展开的工作。
| [1] | Miettinen M, Monihan JM, Sarlomo-Rikala M, et al. Gastrointestinal stromal tumors/smooth muscle tumors (GISTs) primary in the omentum and mesentery: clinicopathologic and immunohistochemical study of 26 cases[J]. Am J Surg Pathol, 1999, 23(9): 1109-18. DOI: 10.1097/00000478-199909000-00015. |
| [2] | Reith JD, Goldblum JR, Lyles RH, et al. Extragastrointestinal (Soft tissue) stromal tumors: An analysis of 48 cases with emphasis on histologic predictors of outcome[J]. Mod Pathol, 2000, 13(5): 577-85. DOI: 10.1038/modpathol.3880099. |
| [3] | Chen CY, Jaw TS, Wu DC, et al. MDCT of giant gastric folds: differential diagnosis[J]. AJR Am J Roentgenol, 2010, 195(5): 1124-30. DOI: 10.2214/AJR.09.3129. |
| [4] | Tsurumaru D, Miyasaka M, Nishimuta YA, et al. Differentiation of early gastric Cancer with ulceration and resectable advanced gastric Cancer using multiphasic dynamic multidetector CT[J]. Eur Radiol, 2016, 26(5): 1330-7. DOI: 10.1007/s00330-015-3938-2. |
| [5] | Iannicelli E, Scavone G, Speranza A, et al. MDCT in GIST evaluation[J]. Clin Ter, 2009, 160(3): 201-6. |
| [6] | Wang JK. Predictive value and modeling analysis of MSCT signs in gastrointestinal stromal tumors (GISTs) to pathological risk degree[J]. Eur Rev Med Pharmacol Sci, 2017, 21(5): 999-1005. |
| [7] | Lee CM, Chen HC, Leung TK, et al. Gastrointestinal stromal tumor: Computed tomographic features[J]. World J Gastroenterol, 2004, 10(16): 2417-8. DOI: 10.3748/wjg.v10.i16.2417. |
| [8] | Kumar V, Gu Y, Basu S, et al. Radiomics: the process and the challenges[J]. Magn Reson Imaging, 2012, 30(9): 1234-48. DOI: 10.1016/j.mri.2012.06.010. |
| [9] | Parmar C, Rios Velazquez E, Leijenaar R, et al. Robust radiomics feature quantification using semiautomatic volumetric segmentation[J]. PLoS One, 2014, 9(7): e102107. DOI: 10.1371/journal.pone.0102107. |
| [10] | Lambin P, Rios-Velazquez E, Leijenaar R, et al. Radiomics: extracting more information from medical images using advanced feature analysis[J]. Eur J Cancer, 2012, 48(4): 441-6. DOI: 10.1016/j.ejca.2011.11.036. |
| [11] | Coroller TP, Grossmann P, Hou Y, et al. CT-based radiomic signature predicts distant metastasis in lung adenocarcinoma[J]. Radiother Oncol, 2015, 114(3): 345-50. DOI: 10.1016/j.radonc.2015.02.015. |
| [12] | Liang CS, Huang YQ, He L, et al. The development and validation of a CT-based radiomics signature for the preoperative discrimination of stage Ⅰ-Ⅱ and stage Ⅲ-Ⅳ colorectal Cancer[J]. Oncotarget, 2016, 7(21): 31401-12. |
| [13] | Zhou Y, He L, Huang YQ, et al. CT-based radiomics signature: a potential biomarker for preoperative prediction of early recurrence in hepatocellular carcinoma[J]. Abdom Radiol (NY), 2017, 42(6): 1695-704. DOI: 10.1007/s00261-017-1072-0. |
| [14] | Zhang Q, Xiao Y, Suo JF, et al. Sonoelastomics for breast tumor classification: a radiomics approach with clustering-based feature selection on sonoelastography[J]. Ultrasound Med Biol, 2017, 43(5): 1058-69. DOI: 10.1016/j.ultrasmedbio.2016.12.016. |
| [15] | Ba-Ssalamah A, Muin D, Schernthaner R, et al. Texture-based classification of different gastric tumors at contrast-enhanced CT[J]. Eur J Radiol, 2013, 82(10): EE43-537. |
| [16] | Ma ZL, Fang MJ, Huang YQ, et al. CT-based radiomics signature for differentiating Borrmann type Ⅳ gastric cancer from primary gastric lymphoma[J]. Eur J Radiol, 2017, 91(3): 142-7. |
| [17] | Sahiner B, Chan HP, Hadjiiski L. Classifier performance prediction for computer-aided diagnosis using a limited dataset[J]. Med Phys, 2008, 35(4): 1559-70. DOI: 10.1118/1.2868757. |
| [18] | Joensuu H. Risk stratification of patients diagnosed with gastrointestinal stromal tumor[J]. Hum Pathol, 2008, 39(10): 1411-9. DOI: 10.1016/j.humpath.2008.06.025. |
| [19] | Haralick RM, Shanmugam K, Dinstein IH. Textural features for image classification[J]. TEEE T Syst Man CY-S, 1973, smc-3(6): 610-21. DOI: 10.1109/TSMC.1973.4309314. |
| [20] | Galloway MM. Texture analysis using gray level run lengths[J]. IEEE Trans Comput Imaging, 1975, 4(2): 172-9. |
| [21] | Thibault G, Fertil B, Navarro C, et al. Texture indexes and gray level size Zone matrix application to cell nuclei classification[J]. PRIP, 2009, 25(4): 140-5. |
| [22] | Amadasun M, King R. Textural features corresponding to textural properties[J]. IEEE Trans Syst Man Cybern, 1989, 19(5): 1264-74. DOI: 10.1109/21.44046. |
| [23] | Vallières M, Freeman CR, Skamene SR, et al. A radiomics model from joint FDG-PET and MRI texture features for the prediction of lung metastases in soft-tissue sarcomas of the extremities[J]. Phys Med Biol, 2015, 60(14): 5471-96. DOI: 10.1088/0031-9155/60/14/5471. |
| [24] | Jiang W, Spurgeon SK, Twiddle JA, et al. A wavelet cluster-based band-pass filtering and envelope demodulation approach with application to fault diagnosis in a dry vacuum pumpProceedings of the Institution of Mechanical Engineers Part C[J]. PI Mech Eng C-J Mec, 2007, 221(11): 1279-86. DOI: 10.1243/09544062JMES544. |
| [25] | Lloyd S. Least squares quantization in PCM[J]. IEEE Trans Inform Theory, 1982, 28(2): 129-37. DOI: 10.1109/TIT.1982.1056489. |
| [26] | Reshef DN, Reshef YA, Finucane HK, et al. Detecting novel associations in large data Sets[J]. Science, 2011, 334(662): 1518-24. |
| [27] | Kinney JB, Equitability AG, mutual information. And the maximal information coefficient[J]. P Natl Acad Sci USA, 2014, 111(9): 3354-9. DOI: 10.1073/pnas.1309933111. |
| [28] | Gillies RJ, Kinahan PE, Hricak H. Radiomics: images are more than pictures, they are data[J]. Radiology, 2016, 278(2): 563-77. DOI: 10.1148/radiol.2015151169. |
| [29] | Ng F, Kozarski R, Ganeshan B, et al. Assessment of tumor heterogeneity by CT texture analysis: Can the largest cross-sectional area be used as an alternative to whole tumor analysis[J]. Eur J Radiol, 2013, 82(2): 342-8. DOI: 10.1016/j.ejrad.2012.10.023. |
| [30] | Johnson PT, Horton KM, Fishman EK. Hypervascular gastric masses: CT findings and clinical correlates[J]. Am J Roentgenol, 2010, 195(6): WW20-415. |
| [31] | Aerts HJ, Velazquez ER, Leijenaar RT, et al. Decoding tumour phenotype by noninvasive imaging using a quantitative radiomics approach[J]. Nat Commun, 2014, 51(4): 4006. |
 2018, Vol. 38
2018, Vol. 38

