2. 南方医科大学 广东省医学图像处理重点实验室,广东 广州 510515
2. Guangdong Provincial Key Laboratory of Medical Image Processing, Southern Medical University, Guangzhou, 510515, China
近年来,乳腺癌的发病率一直呈现上升趋势[1],乳腺筛查成为了降低乳腺癌死亡率的重要手段[2-3]。
X线乳腺摄影技术[4]对微小病灶具有高度敏感性,但传统的全视野数字乳腺X摄影(FFDM)由于平面二维成像的组织重叠效应在乳腺肿瘤的检测中存在一定程度的检出失败率[5-6],同时,由正常组织重叠而产生的假阳性肿瘤会误导医生的诊断。近年来,数字乳腺层析成像(DBT)逐渐在临床中得到广泛应用[7-8],DBT成像利用传统的X线源,以平板探测器为旋转中心采集一定数量的投影数据,并通过有限数量的投影数据进行三维重建,实现了乳腺的三维成像。数字乳腺层析成像很大程度上解决了二维成像组织重叠所导致的检出失败和假阳性误诊的问题[9]。同时,相对于CT成像技术,DBT成像很大程度上降低了患者的辐射剂量[10],但乳腺作为一个对X射线敏感器官[11],其辐射危害仍然不容小觑。为进一步降低辐射剂量,可以通过降低X射线球管电流(mAs)来实现超低剂量DBT成像[12],但超低剂量扫描条件下的重建图像噪声水平较高,导致低对比度病灶及微小钙化点难以识别。
为抑制DBT图像噪声,提高病灶检出率,本文借鉴低剂量CT成像中的投影数据降噪理论[13-16]对投影数据进行恢复后重建,并在噪声模型构建和恢复算法设计两个方面做了改进,以此提升投影数据恢复效果和重建图像质量。在噪声模型构建方面,Ma等[17]在对投影数据的方差分析过程中发现低剂量扫描条件下电子噪声的忽略会使测量投影数据的方差估计与真实值产生较大差距,并提出和验证了精确化的噪声模型,本文基于这一理论将常规的近似噪声模型做了精确化处理,用于低剂量DBT投影数据恢复。同时,我们发现基于平板探测器获取的投影数据存在噪声相关性[18]。基于上述,本文充分利用DBT平板探测器的数据统计特性,在对DBT投影数据进行精确噪声建模(对投影数据进行方差特性统计)的基础上,结合噪声相关性构建惩罚加权最小二乘算法对投影图像进行数据优化。最后利用改进的FBP算法进行图像重建,以提升DBT图像质量。
1 方法 1.1 投影数据噪声建模对于图像噪声的准确建模,探测器响应的数据统计尤为重要。Whiting等人对能量积分型探测器数据校正以及数据采集的随机过程进行理论建模,得出校正后数据满足复合泊松分布的结论[19-20],透射光子分布函数将量子噪声与背景电子噪声结合,定义为:
| $ {\tilde I_i} \sim \sum\limits_k {G({E_k})Pois\;{\rm{son}}\{ {{\tilde \lambda }_i}({E_k})\} + Normal\{ {d_i}, {\sigma _{e, i}}^2\} } $ | (1) |
i表示探测单元序列编号,参数k表示X光能量级,G(.)表示能谱概率,Possion{.}表征数据的泊松统计特性,其中λ代表穿过测量体后的光子平均数,即探测器实际接收到的信号。公式(1)的第二项表征电子噪声,服从均值为di,方差为σe, i2的高斯分布,电子噪声的参数可以通过暗电流数据测量。对于复合泊松分布,目前还还缺闭合、准确的似然函数,本文忽略X光多能特性,将X线光子分布函数简化为:
| $ {{\tilde I}_i} \sim Pois\;{\rm{son}}\{ {\lambda _i}\} + Normal\{ {d_i}, {\sigma _{e, i}}^2\} $ | (2) |
利用朗伯比尔定律对探测器数据进行对数变换,可以得到探测单元i对应路径上的线性衰减系数线积分数据:
| $ {p_i} = \ln \frac{{{I_{{o_i}}}}}{{{{\tilde I}_i}}} = \ln {I_{{o_i}}}-\ln {{\tilde I}_i} $ | (3) |
式(3)中,Ioi为入射(没有经过测量体之前)光子数目,可以通过空扫描进行测量;
| $ \sigma _{pi}^2 = {\mathop{\rm var}} ({p_i}) = \frac{1}{{{\lambda _i}}}(1 + \frac{{{\sigma _{e, i}}^2-1.25}}{{{\lambda _i}}}) $ | (4) |
式中λi = Ioiexp(-pi)。式(4)给出了投影数据方差和光子平均数、电子噪声方差的关系,保留了量子噪声和电子噪声对方差特性的影响。
1.2 基于噪声相关性的惩罚加权最小二乘算法在DBT投影数据恢复中的应用基于先前对平板探测器的噪声相关性的研究,在同一扫描条件下,对大量重复的平板探测器投影数据统计分析,得出相邻投影数据之间存在着噪声相关性的结论,不同路径积分数的噪声相关性可由相关因子βij描述:
| $ {\rho _{ij}} = \frac{{{\mathop{\rm cov}} ({p_i}, {p_j})}}{{{\sigma _i}{\sigma _j}}} = \frac{{{\mathop{\rm cov}} ({p_i}, {p_j})}}{{\sqrt {{\mathop{\rm var}} ({p_i})} \sqrt {{\mathop{\rm var}} ({p_j})} }} $ | (5) |
基于式(5)中测定的相关系数,利用式(4)中对投影数据噪声方差的估计,我们可以获得cov(pi, pj) = σij = ρij∙
| $ \Phi (p) = (\hat y-p)'{\sum ^{-1}}(\hat y-p) + \beta R(p) $ | (6) |
式(6)中第一项为数据保真项,其中
| $ R(p) = \sum\limits_j {R({p_j}) = \sum\limits_j {\sum\limits_{k \in {S_j}} {w(k, j){{({p_j}-{p_k})}^2}} } } $ | (7) |
Sj指在二维投影数据中与像素j最相邻的4个像素,本文中4个像素的权w(k, j)取相同值。通过最小化代价函数(6)可以得到优化的线积分投影数据:
| $ \begin{array}{l} \hat p = \arg \;\mathop {\min }\limits_{\mu \ge 0} (\hat y-p)'{\sum ^{-1}}(\hat y-p) + \\ \beta \sum\limits_j {\sum\limits_{k \in {S_j}} {w(k, j){{({p_j} - {p_k})}^2}} } \end{array} $ | (8) |
本文中协方差矩阵的非负对称特性以及惩罚先验项R(p)的二次平滑设计使得式(8)中的代价函数为凸函数。由凸函数的性质,我们可以将对Φ(p)的最优化转化为求解▽Φ(p) = 0的极值问题,且该解理论上是唯一的。将▽R(p)改写为▽R(p) = ▽‖p‖2 = Ap。A为与数据协方差矩阵结构类似的五对角矩阵,满足:
| $ {A_{ij}} = \left\{ \begin{array}{l} 4, \;\;\;\;\;\;\;\;\;\;\;i = j\\ -1, \;\;\;\;\;\;\;i-j = \pm 1\;or\;i-j = \pm B\\ 0, \;\;\;\;\;\;\;\;\;\;o\;{\rm{th}}\;erwise \end{array} \right. $ | (9) |
因此代价函数的梯度形式可以通过下式改写:
| $ \begin{array}{l} \nabla \Phi (p) = \nabla ({(y-p)^T}{\sum ^{-1}}(y-p)) + \beta \nabla R(p) = 0\\ \Rightarrow {\sum ^{ - 1}}(p - y)) + \beta Ap = 0 \end{array} $ | (10) |
由此,我们可以通过解∑-1(p -y)+ βAp = 0最优化求解式(8)。
为了充分利用矩阵∑和A的稀疏结构,我们可以利用LSQR算法进行迭代求解。对∑-1(p -y)+ βAp = 0迭代求解过程如下:
0.初始化p(0),并设定迭代终止条件ε;
1.求解线性方程∑b = y -p(n),以更新b;
2.对步骤1求解得到的b值,求解线性方程βAp(n + 1) = b,得到p(n + 1);
3.当满足|p(n + 1) -p(n)| < ε停止迭代,否则返回步骤1;
*其中b为中间变量
1.3 恢复投影数据重建对恢复后的投影数据,本文利用三维的滤波反投影(FBP)算法进行重建[21-22]。重建算法基于滤波反投影,为实现乳腺的最佳成像效果改进滤波设计,同时采用距离坐标变换后再进行反投影(距离驱动反投影,DDBP)[23],这样的方式相比传统的对整个图像基于路径的反投影缩短了计算时间,从精度的角度出发,距离坐标变换反投影考虑了图像像素和探测器的宽度问题,可以忽略将投影数据的锥形束近似平行束处理时对重建的影响。
2 结果 2.1 实验数据获取本文主要采用DBT实验原型机采集的ACR标准体模投影数据进行图像重建。ACR标准体模是乳腺成像所使用的标准测试体模,体模内部包含与乳腺结构相似衰减系数的物质,对应于乳腺的腺体、纤维组织、钙化点、囊肿等结构,ACR标准体模结构信息参见图 1。

|
图 1 乳腺成像标准体膜ACR体模内部结构信息及实物图 Figure 1 Internal structure and appearance of an ACR standard phantom. |
数据采集系统为Analogic公司AXS-2430平板探测器,投影数据的采集参数为:管电压30 kV,管电流分别是40、60、80、100 mA。探测器以与X线源曝光相同的时序采集25个投影,X线源在±24°范围内每隔2°曝光1次。数据采集的过程中,X线源到探测器的距离为650 mm,旋转中心到探测器的距离为25 mm。原始投影数据大小为3584×2816,像素大小为0.085 mm× 0.085 mm。
2.2 评价参数为定量评价算法性能,本文中我们选用局部信噪比和对比度信噪比作为图像质量的评估指标,其中,局部信噪比(LSNR)和对比度信噪比(CNR)分别定义为:
| $ LSNR = \bar f/{\sigma _f} $ | (11) |
| $ CNR = \frac{{2\left| {\bar f-\bar b} \right|}}{{{\sigma _f} + {\sigma _b}}} $ | (12) |
式(11)和(12)中,f, b分别表示感兴趣区域(ROI)和背景区域内的像素均值,σf, σb为感兴趣区域(ROI)和背景区域内的标准差。
2.3 投影图像恢复前后比较本文的方法实现过程中,首先通过暗扫描对电子噪声方差进行估计,再结合公式(4)进行投影数据的方差估计。图 2给出了0角度下利用基于噪声相关性的惩罚加权最小二乘法恢复前后的投影图像。其中图 2中A、B的扫描参数为30 kV、40 mA,C、D的扫描参数为30 kV、60 mA,图A和图C为被噪声污染的投影图像,图B和图D为利用本文算法恢复后图像。

|
图 2 30 kVp、40 mA和30 kVp、60 mA剂量下0角度投影数据恢复前后的图像. Figure 2 Original and restored projection images at angle 0 with different scan settings. A: Original projection image obtained at 30 kVp and 40 mA; B: Restored projection image obtained at 30 kV and 40 mA; C: Original projection image obtained at 30 kV and 60 mA; D: Restored projection image obtained at 30 kV and 60 mA. |
对比不同剂量下的投影图像,可以看出低剂量扫描会导致投影数据存在严重的噪声,利用基于噪声相关性的惩罚加权最小二乘算法,低剂量投影图像的噪声得到有效的抑制,投影图像无失真。
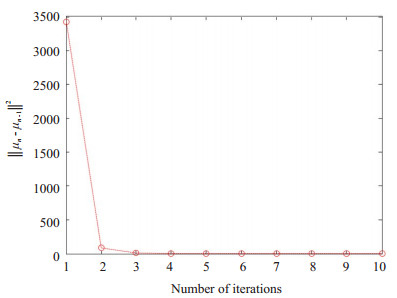
图 3展示了30 kV,40 mA剂量下的0角度投影数据在参数β = 1200时本文算法迭代的收敛情况,横轴表示迭代步数,纵轴量‖ μn -μn -1‖2可以表征第n步与第n -1步迭代后投影数据结果之间的差异,从图中可以看出本文算法收敛速度较快,10步迭代即可获取稳定结果。
|
图 3 0角度实验数据在30 kVp、40 mA剂量下,参数β = 1200时,PWLS算法的收敛测试图 Figure 3 Convergence of PWLS algorithm at 30 kVp and 40 mA at the angle of 0 with β=1200. |
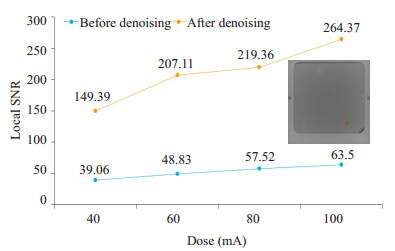
本文中,我们对0角度下的投影数据进行了LSNR对比分析,图 4中折线图展示了不同剂量投影图像恢复前后的LSNR值,从图中我们可以看出,基于噪声相关性的惩罚加权最小二乘算法可以有效地抑制DBT投影图像噪声,提高投影图像的信噪比。
|
图 4 0角度下40、60、80、100 mA四个剂量的投影数据恢复前后局部信噪比折线图 Figure 4 Local SNRs calculated from projection data at angle 0 and at the dose levels of 40, 60, 80 and 100 mA before and after denoising. |
利用距离驱动反投影(DDBP)[9]算法对恢复后投影图像进行重建,我们可以得到如图 5所示的重建图像。图 5A~H分别给出了40、60、80、100 mA四个剂量下原始投影数据重建图像和恢复投影数据重建图像。

|
图 5 不同剂量下投影数据恢复前后的重建结果 Figure 5 Reconstruction results before and after projection data recovery at different doses. A: The image reconstructed from original projections at 30 kVp and 40 mA; B: The image reconstructed from the restored projections at 30 kVp and 40 mA; C: The image reconstructed from original projections at 30 kVp and 60 mA; D: The image reconstructed from the restored projections at 30 kVp and 60 mA; E: The image reconstructed from original projections at 30 kVp and 80 mA; F: The image reconstructed from the restored projections at 30 kVp and 80 mA; G: The image reconstructed from original projections at 30 kVp and 100 mA; H: The image reconstructed from the restored projections at 30 kVp and 100 mA. |
从重建结果中我们可以看出,利用原始投影数据重建图像中含有大量噪声,点状细节被噪声淹没无法识别,同时图像的对比度也十分有限;而利用恢复投影数据重建的图像中,噪声水平较低,点状细节得到凸显。相对于图A和C,图B和D中第三级点状结构可以很好的重建并显现出来,相对于图E和G,图F和H中第四级点状结构可以很好的重建并显现出来;由此可见,利用基于噪声相关性的惩罚加权最小二乘算法可以实现低剂量DBT图像的有效去噪,提高DBT图像的对比度。
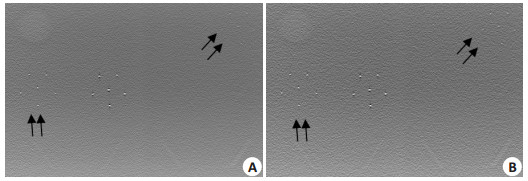
为展示本文算法的有效性,我们采用BM3D(Block Matching 3-Dimension)滤波算法[24-25]用于投影数据恢复,然后对恢复数据进行FBP重建。图 6中展示了40 mA剂量下BM3D及本文方法重建的DBT图像,可以看出图 6B中点状结构清晰度明显优于图 6A对应级数点状结构。此实验结果说明,本文的算法在图像细节结构保持方面有上佳表现。
|
图 6 不同算法对40 mA投影数据处理后的重建图像. Figure 6 Reconstructed images from restored projection data (40 mA) using different algorithms. A: BM3D; B: the proposed method. |
为进一步说明方法的有效性,我们分别计算了四个剂量下本文算法重建图像与图 7所示的相同感兴趣区的LSNRs和CNRs。表 1和表 2分别给出了不同剂量下投影数据恢复前后的重建图像的LSNR及CNR值。从表格中数据可以看出,随着剂量的升高,重建DBT图像的LSNR及CNR值变高;相对于原始投影数据重建结果,利用PWLS算法恢复投影数据重建图像有更高的LSNR和CNR。

|
图 7 局部信噪比(LSNR)和对比度信噪比(CNR)感兴趣区域图 Figure 7 Analysis of LSNR and CNR in the region of interest (ROI). The red and blue boxes indicate the ROIs for LSNR and CNR analysis, respectively |
| 表 1 不同剂量下投影数据恢复前后的重建图像对比度信噪比(CNR) Table 1 CNRs calculated from the reconstruction results before and after projection data recovery at different doses |
| 表 2 不同剂量下投影数据恢复前后的重建图像局部信噪比(LSNR) Table 2 LSNRs calculated from the reconstruction results before and after projection data recovery at different doses |
乳腺筛查的重大需求决定了数字乳腺层析成像这一新兴X射线成像技术在临床应用上的重要意义。然而,噪声的存在可能掩盖某些低对比度的病灶区域,在图像断层重建的去噪研究中,基于最小二乘算法的去噪方法得到了广泛关注[16, 26]。本方法借鉴了前人成果低剂量CT成像中的投影数据降噪算法,但采用了更加精确地噪声模型并结合噪声相关性构建惩罚加权最小二乘算法对投影图像进行数据优化,对于噪声模型的改进,Liang等人在对投影数据的方差分析过程中发现,噪声分布模型的正态拟合与实际情况存在一定差距[17],在扫描剂量较高的情况下,探测器系统所导致的电子噪声对探测器测量的投影数据影响极低,因此可以忽略不计,但是在低剂量扫描条件下,忽略电子噪声会使测量值的方差估计与真实值产生较大差距,本方法针对低剂量DBT投影数据的噪声进行恢复,噪声模型的精确化无疑使降噪效果更加显著。
将噪声相关性推论得到的数据方差特性用于最小二乘算法中可以优化数据恢复结果。DBT成像所用的球管及管电压相对CT成像略有不同[27],但单一角度下DBT投影数据与CT投影数据的产生机制并无本质差异。在数据采集过程中,DBT采用了平板探测器,不同探测器单元上的投影数据可能相互影响。本文对投影数据进行方差特性统计,并结合噪声相关性构建惩罚加权最小二乘算法对投影图像进行数据优化,利用改进的FBP算法重建,以提升DBT重建图像质量。参照CT成像中噪声模型构建方法,将电子噪声和量子噪声结合构建加权最小二乘算法来对噪声进行去除。通过合理的代价函数优化及选取合适的参数,投影图像恢复结果及重建DBT结果均显示,基于噪声相关的惩罚加权最小二乘算法在低剂量DBT成像中有着上佳表现,不同剂量图像的局部信噪比和对比度信噪比提升约3.6倍。同时,为进一步说明算法的有效性,实验中我们加入了BM3D滤波算法[24-25]对投影数据进行去噪处理,而后进行基于FBP的DBT重建。重建结果显示,在图像细节结构保持方面,本文算法优于BM3D算法。
本文对恢复后的投影数据采用了距离驱动反投影(DDBP)算法进行重建,DDBP算法相比传统的对整个图像基于路径的反投影缩短了计算时间[24],与此同时,从精度的角度出发,DDBP算法考虑了图像像素和探测器的宽度问题,可以忽略将投影数据的锥形束近似平行束处理时对重建的影响。
总体来说,通过对不同剂量下的乳腺体模数据的研究对比显示,基于噪声相关性的惩罚加权最小二乘算法可以用于低剂量DBT成像投影数据降噪,该应用使低剂量的乳腺层析图像不再妥协于低图像质量,为乳腺层析技术的进一步发展提供了技术支持。
| [1] | 陈万青, 郑荣寿. 中国女性乳腺癌发病死亡和生存状况[J]. 中国肿瘤临床, 2015, 42(13): 668-74. |
| [2] | Poplack SP, Tosteson TD, Kogel CA, et al. Digital breast tomosynthesis: initial experience in 98 women with abnormal digital screening mammography[J]. Am J Roentgenol, 2007, 189(3): 616-23. DOI: 10.2214/AJR.07.2231. |
| [3] | Alhajj M, Wicha MS, Benitohernandez A, et al. Prospective identification of tumorigenic breast cancer cells[J]. P Natl Acad Sci USA, 2003, 100(7): 3983-8. DOI: 10.1073/pnas.0530291100. |
| [4] | 曹厚德, 蒋琴. 乳腺X线摄影若干技术要素的研究[J]. 中华放射学杂志, 2000, 34(3): 155-8. |
| [5] | Van Engeland S, Snoeren PR, Huisman H, et al. Volumetric breast density estimation from full-field digital mammograms[J]. IEEE T Med Imaging, 2006, 25(3): 273-82. DOI: 10.1109/TMI.2005.862741. |
| [6] | 张莉, 洪常华. DBT与FFDM对致密型乳腺病变诊断对比分析[J]. 医学影像学杂志, 2016, 26(8): 1536-8. |
| [7] | Skaane P, Gullien R, Bjørndal H, et al. Digital breast tomosynthesis (DBT): initial experience in a clinical setting[J]. Acta Radiol, 2012, 53(5): 524-9. DOI: 10.1258/ar.2012.120062. |
| [8] | Chen SC, Carton AK, Albert M, et al. Initial clinical experience with contrast-enhanced eigital breast tomosynthesis[J]. Acad Radiol, 2007, 14(2): 229-38. DOI: 10.1016/j.acra.2006.10.022. |
| [9] | Svahn TM. Letter to the Editor re: Diagnostic accuracy of digital breast tomosynthesis versus digital mammography for benign and malignant lesions in breasts: a meta-analysis[J]. Eur Radiol, 2014, 24(4): 928-9. DOI: 10.1007/s00330-013-3092-7. |
| [10] | Karellas A, Lo JY, Orton CG. Cone beam x-ray CT will be superior to digital x-ray tomosynthesis in imaging the breast and delineating cancer[J]. Med Phys, 2008, 35(2): 409-11. DOI: 10.1118/1.2825612. |
| [11] | Sakurai T, Kawamata R, Kozai Y, et al. Relationship between radiation dose reduction and image quality change in photostimulable phosphor luminescence X-ray imaging systems[J]. Dentomaxillofac Rad, 2010, 39(4): 207-15. DOI: 10.1259/dmfr/44413341. |
| [12] | Gur D, Zuley ML, Anello MI, et al. Dose reduction in digital breast tomosynthesis (DBT) screening using synthetically reconstructed projection images: an observer performance study[J]. Acad Radiol, 2012, 19(2): 166-71. DOI: 10.1016/j.acra.2011.10.003. |
| [13] | Manduca A, Yu L, Trzasko JD, et al. Projection space denoising with bilateral filtering and CT noise modeling for dose reduction in CT[J]. Med Phys, 2009, 36(11): 4911-9. DOI: 10.1118/1.3232004. |
| [14] | Liao Z, Hu S, Li M, et al. Noise Estimation for single-slice sinogram of low-dose X-ray computed tomography using homogenous patch[J]. Math Probl Eng, 2011, 2012(2): 208-12. |
| [15] | 田秀梅, 黄静, 林嘉慧. 投影数据恢复方法在低剂量脑灌注CT成像中的应用[J]. 南方医科大学学报, 2017, 37(4): 470-4. |
| [16] | Wang J, Li T, Lu H, et al. Penalized weighted least-squares approach to sinogram noise reduction and image reconstruction for low-dose X-ray computed tomography[J]. IEEE T Med Imaging, 2006, 25(10): 1272-83. DOI: 10.1109/TMI.2006.882141. |
| [17] | Ma J, Liang Z, Fan Y, et al. Variance analysis of x-ray CT sinograms in the presence of electronic noise background[J]. Med Phys, 2012, 39(7): 4051-65. |
| [18] | Zhang H, Ouyang L, Ma J, et al. Noise correlation in CBCT projection data and its application for noise reduction in low-dose CBCT[J]. Med Phys, 2014, 41(3): 1-10. |
| [19] | Whiting BR, Massoumzadeh P, Earl OA, et al. Properties of preprocessed sinogram data in x-ray computed tomography[J]. Med Phys, 2006, 33(9): 3290-303. DOI: 10.1118/1.2230762. |
| [20] | Huang SY, Yang K, Abbey CK, et al. A semiempirical linear model of indirect, flat-panel x-ray detectors[J]. Med Phys, 2012, 39: 2108-18. DOI: 10.1118/1.3691180. |
| [21] | Wu T, Moore RH, Rafferty EA, et al. A comparison of reconstruction algorithms for breast tomosynthesis[J]. Med Phys, 2004, 31(9): 2636-47. DOI: 10.1118/1.1786692. |
| [22] | Park Y, Park C, Cho H, e t, a l. Image reconstruction for digital breast tomosynthesis (DBT) by using projection-angle-dependent filter functions[J]. J Korean Phys Soc, 2014, 65(5): 763-9. DOI: 10.3938/jkps.65.763. |
| [23] | De Man B, Basu S. Distance-driven projection and backprojection in three dimensions[J]. Phys Med Biol, 2004, 49(11): 2463-75. DOI: 10.1088/0031-9155/49/11/024. |
| [24] | Danielyan A, Katkovnik V, Egiazarian K O, et al. BM3D frames and variational image deblurring[J]. IEEE T Image Process, 2012, 21(4): 1715-28. DOI: 10.1109/TIP.2011.2176954. |
| [25] | Yang FQ, Zhang DH, Huang KD, e t, a l. Image artifacts and noise reduction algorithm for cone-beam computed tomography with lowsignal projections[J]. J X-Ray Sci Technol, 2017(9): 1-14. |
| [26] | Liu Y, Ma J, Zhang H, et al. Low-mAs X-ray CT image reconstruction by adaptive-weightedTV-constrained penalized re-weighted leastsquares[J]. J X-Ray Sci Technol, 2014, 22(4): 437-57. |
| [27] | Gong X, Glick SJ, Liu B, et al. A computer simulation study comparing lesion detection accuracy with digital mammography, breast tomosynthesis and cone-beam CT breast imaging[J]. Med Phys, 2006, 33(4): 1041-52. DOI: 10.1118/1.2174127. |
 2018, Vol. 38
2018, Vol. 38

