X射线计算机断层成像(CT)因其在时间、空间分辨率上的卓越表现,已经广泛应用于临床诊断和治疗。CT图像的质量与X射线辐射剂量密切相关,剂量越高图像质量越好,然而,过量的X射线照射又会诱发恶性肿瘤、白血病以及其他遗传性疾病[1]。当前,临床上采用低剂量的CT扫描方案虽然能在一定程度上减少X射线的照射剂量,但采集到的投影数据会含有较高的噪声,直接滤波反投影重建图像的质量往往无法满足临床诊断的需要[2]。因此,如何在降低X射线辐射剂量的同时保证图像质量已经成为CT成像领域的迫切要求。
为了降低X射线的辐射剂量,许多优化的低剂量CT扫描方案[3-5]以及抑制噪声和伪影的重建算法[6-15]相继被提出。目前,直接降低管电流、管电压或者减少扫描角向采样数目是实现低剂量CT扫描最简单且最有效的方法。但是,降低管电流会导致投影数据中光子噪声大幅增加而且电子噪声的影响也会更加突出;降低管电压则会因X射线的穿透能力下降造成射束硬化效应;减少扫描角向采样数目使得投影数据不满足香农采样定理而造成重建图像产生严重的条形伪影。不同于传统的滤波反投影算法,基于低剂量CT投影数据恢复的图像重建方法对CT成像系统进行精确建模(包括X线源、探测器、电子噪声、成像物体等),可以实现优质的低剂量CT图像重建[16-22]。其目标函数是根据测量数据的噪声特性来构建的,通常包含两项,即数据保真项和正则化项,前者用于描述投影数据的统计特性,后者用于修正解的特性。在图像分段常量的假设下,全变分(TV)正则化模型[23-24]其在去除噪声的同时可以保持图像的边缘信息。然而,许多临床CT图像并不是完全满足分段常量的假设,在剂量特别低时或者投影角度特别少时,TV重建的图像会产生阶梯效应和块状伪影。因此TV正则化在基于投影数据恢复的低剂量CT重建中会失去效力。为了解决这个问题,本文提出一个基于全广义变分(TGV)正则化的低剂量CT重建算法,其可以在投影数据不满足分段常数假设的前提下去除噪声和条形伪影。
本文结构安排形式如下:介绍Anscombe变换公式、全广义变分概念和基于全广义变分最小化恢复模型以及解此模型的优化算法;对Clock体模和SheppLogan体模实验结果定性和定量的分析,来验证所提出方法的有效性;对本文所提出的方法进行总结和讨论。
1 方法 1.1 Anscombe变换低剂量CT成像系统中,探测数据可以描述为I = I0exp(-u),其中I0为X射线入射光子的数目,I为出射光子的数目并且服从Poisson分布[25],u表示经过对数变换后的投影数据,即Sinogram (正弦图)。
服从Poisson分布的数据可以通过Anscombe变换[26]使其变为近似服从Gaussian分布的数据。假设x服从Poission分布,通过如下的Anscombe变换:
| $ y\left( x \right) = 2\sqrt {x + \frac{3}{8}} $ | (1) |
我们可以将服从Poission分布的x变换成近似服从方差为1的Gaussian分布[26]。
假设投影数据每个像素间是互相独立的,并且经过Anscombe变换后都服从方差为1的Gaussion分布,令f= (f1, f2, …, fn)T为待估计投影数据的理想值, u = (u1, u2, …, un)T表示投影数据经过Anscombe变化后近似满足Gaussian分布的数据,其中表示转置运算。
1.2 全广义变分(TGV)TGV正则化模型由Berdies等[27, 29]提出并用于图像去噪。给定图像f,k阶TGV的定义为:
| $ \begin{array}{l} TGV_\alpha ^k\left( f \right) = \sup \left\{ {\int_\Omega {u{\rm{di}}{{\rm{v}}^k}v{\rm{d}}x\left| {v \in C_c^k\left( {\Omega ,Sy{m^k}\left( {{R^d}} \right)} \right)} \right.} ,} \right.\\ \left. {{{\left\| v \right\|}_\infty } \le {\alpha _0},{{\left\| {{\rm{div}}\;v} \right\|}_\infty } \le {\alpha _1}} \right\} \end{array} $ | (2) |
其中,l = 0, …, k -1, k ∈ N是TGV的阶数,α = (α0,α1,…,αk -1)是TGV的权重。Symk(Rd)是k阶对称张量空间,l阶散度算子定义是:
| $ {\rm{di}}{{\rm{v}}^l}v = {\Sigma _{\gamma \in {M_l}}}\frac{{l!}}{{\gamma !}}\frac{{{\partial ^l}{v_{\eta + \gamma }}}}{{\partial {x^\gamma }}},\eta \in {M_{k - 1}} $ | (3) |
其中,
| $ {\left\| v \right\|_\infty } = \mathop {\sup }\limits_{x \in \Omega } \left\{ {{{\left( {\sum\limits_{\eta \in {M_k}} {\frac{{k!}}{{\eta !}}{v_\eta }{{\left( x \right)}^2}} } \right)}^{\frac{1}{2}}}} \right\} $ | (4) |
当k = 1时,TGV和TV是等价,即可以表示为:TGVαk = α0TV。在本文中,我们只考虑二阶TGV,定义为:
| $ \begin{array}{l} TGV_\alpha ^2\left( f \right) = \sup \left\{ {\int_\Omega {u{\rm{di}}{{\rm{v}}^2}v{\rm{d}}x\left| {v \in C_c^2\left( {\Omega ,{S^{d \times d}}} \right)} \right.} ,} \right.\\ \left. {{{\left\| v \right\|}_\infty } \le {\alpha _0},{{\left\| {{\rm{div}}\;v} \right\|}_\infty } \le {\alpha _1}} \right\} \end{array} $ | (5) |
其中,Sd×d是d×d维矩阵空间,α = (α0,α1)是正数,进一步,对称矩阵的一阶和二阶散度可以由下式表示:
| $ {\left( {{\rm{div}}\;v} \right)_i} = \sum\limits_{j = 1}^d {\frac{{\partial {v_{ij}}}}{{\partial {x_j}}}} ,{\rm{di}}{{\rm{v}}^2}v = \sum\limits_{i = 1}^d {\frac{{{\partial ^2}{v_{ii}}}}{{\partial x_i^2}}} + 2\sum\limits_{i < j} {\frac{{\partial {v_{ij}}}}{{\partial {x_i}\partial {x_j}}}} $ | (6) |
类似的,(5)式中的无穷范数定义为:
| $ {\left\| v \right\|_\infty } = \mathop {\sup }\limits_{x \in \Omega } {\left( {\sum\limits_{i = 1}^d {{{\left| {{v_{ii}}\left( x \right)} \right|}^2}} + 2\sum\limits_{i < j} {{{\left| {{v_{ij}}\left( x \right)} \right|}^2}} } \right)^{\frac{1}{2}}} $ | (7) |
| $ {\left\| {{\rm{div}}\;v} \right\|_\infty } = \sup {\left( {\sum\limits_{i = 1}^d {{{\left| {\sum\limits_{j = 1}^d {\frac{{\partial {v_{ij}}}}{{\partial {x_j}}}\left( x \right)} } \right|}^2}} } \right)^{\frac{1}{2}}} $ | (8) |
其中,文献[27]给出了与式(5)互相等价的二阶TGV的定义:
| $ TGV_\alpha ^2\left( f \right) = \mathop {\min }\limits_\omega {\alpha _1}\int_\Omega {\left| {\nabla f - \omega } \right|dx} + {\alpha _0}\int_\Omega {\left| {\varepsilon \left( \omega \right)} \right|dx} $ | (9) |
其中,
投影数据恢复的一般模型[22]可以表示为:
| $ \tilde f = \mathop {\arg }\limits_f \min \frac{1}{2}\left\| {u - f} \right\|_2^2 + \lambda R\left( f \right) $ | (10) |
其中,第1项为数据保真项,第2项为正则化项, λ>0是正则化参数。
本文用TGV正则化代替式(10)中的正则化项R(f), 得到基于TGV最小化的理想数据恢复模型为:
| $ \tilde f = \mathop {\arg }\limits_f \min \frac{1}{2}\left\| {u - f} \right\|_2^2 + \lambda TGV\left( f \right) $ | (11) |
其中,是正则化参数。
公式(11)的离散形式为:
| $ \mathop {\min }\limits_{f \in F,\omega \in W} \frac{1}{2}\left\| {u - f} \right\|_2^2 + {\beta _1}{\left\| {\nabla f - \omega } \right\|_1} + {\beta _0}{\left\| {\varepsilon \left( \omega \right)} \right\|_1} $ | (12) |
其中,F = RN×N, W = R2N×N以及微分算子div,ε,∇可以由限差分算子近似得到[29]。
根据对偶原理[23],我们可以将(12)转化为如下的鞍点问题:
| $ \mathop {\min }\limits_{f \in F,\omega \in W} \mathop {\max }\limits_{p \in P,q \in Q} \frac{1}{2}\left\| {u - f} \right\|_2^2 + {p^{\rm{T}}}\left( {\nabla f - \omega } \right) + {q^{\rm{T}}}\varepsilon \left( \omega \right) $ | (13) |
其中,p和q为对偶变量,并且P和Q定义为:
| $ P = \left\{ {p \in {R^{2N \times N}}\left| {{{\left\| p \right\|}_\infty } \le {\beta _1}} \right.} \right\} $ | (14) |
| $ Q = \left\{ {q \in {R^{3N \times N}}\left| {{{\left\| q \right\|}_\infty } \le {\beta _0}} \right.} \right\} $ | (15) |
| $ pro{j_P}\left( {\tilde p} \right) = \frac{{\tilde p}}{{\max \left( {1,\left| {\tilde p} \right|/{\beta _1}} \right)}} $ | (16) |
| $ pro{j_Q}\left( {\tilde q} \right) = \frac{{\tilde q}}{{\max \left( {1,\left| {\tilde q} \right|/{\beta _0}} \right)}} $ | (17) |
| $ pro{x_1}\left( {\tilde f} \right) = \mathop {\arg \min }\limits_{f \in F} \frac{{\left\| {f - u} \right\|_2^2}}{2} + \frac{{\left\| {f - \tilde f} \right\|_2^2}}{{2\tau }} $ | (18) |
由上述方法求出(11)式的解并对其进行Anscombe逆变换,最后由滤波反投影算法进行重建。
下面我们给出基于TGV正则化的低剂量CT重建方法的计算步骤:
步骤1对低剂量CT投影数据进行Anscombe变换,将服从Poission分布的投影数据转化为近似Gaussian分布的数据。
步骤2基于全广义变分最小化模型,我们使用Chambolle-Pock算法[30]求解,从而达到对Anscombe变换后投影数据去噪的目的。
(1) 初始化参数:β0,β1,τ,ρ;
(2) 初始化变量:p0,q0,ω0,ϖ0,f0,f0;
(3) 对数据进行迭代恢复,迭代形式如下:
| $ \begin{array}{l} For\;\;\;\;n = 0,1, \cdots ,N\\ \;\;\;\;\;\;\;\;\;{p^{n + 1}} = pro{j_P}\left( {{p^n} + \rho \left( {\nabla {{\bar f}^n} - {{\bar \omega }^n}} \right)} \right),\\ \;\;\;\;\;\;\;\;\;{q^{n + 1}} = pro{j_Q}\left( {{q^n} + \rho \varepsilon \left( {{{\bar \omega }^n}} \right)} \right),\\ \;\;\;\;\;\;\;\;\;{f^{old}} = {f^n},\\ \;\;\;\;\;\;\;\;\;{f^{n + 1}} = prox_1^\tau \left( {{f^n} + \tau {\rm{di}}{{\rm{v}}_1}{p^{n + 1}}} \right),\\ \;\;\;\;\;\;\;\;\;{{\bar f}^{n + 1}} = 2{f^{n + 1}} - {f^{old}},\\ \;\;\;\;\;\;\;\;\;{\omega ^{old}} = {\omega ^n},\\ \;\;\;\;\;\;\;\;\;{\omega ^{n + 1}} = {\omega ^n} + \tau \left( {{p^{n + 1}} + {\rm{di}}{{\rm{v}}_2}{q^{n + 1}}} \right),\\ \;\;\;\;\;\;\;\;\;{{\bar \omega }^{n + 1}} = 2{\omega ^{n + 1}} - {\omega ^{old}},\\ End \end{array} $ |
步骤3对步骤2得到的数据其进行Anscombe逆变换,得到去噪后的投影数据。
步骤4对步骤3得到的投影数据进行FBP重建得到CT图像。
2 实验与分析为了验证全广义变分最小化方法在低剂量CT图像重建中的有效性,本文通过Clock和Shepp-Logan数值体模进行定量和定性分析。并且与斜波滤波反投影算法、汉宁滤波反投影算法和非单调全变分最小化算法[28]进行比较。CT成像几何采用弧形探测器的扇形束,其中射线源到旋转中心和探测器的距离分别为570 mm和1040 mm,旋转角在[0, 2π]间的采样值为1160,探测器个数为672。体模大小设定为512×512,对于Clock体模,入射光子数为5.0×104;相应的Shepp-Logan体模的入射光子数为1.0×105。
2.1 Clock体模实验Clock体模实验结果如图 1所示。其中,图 1A为真实的体模图像;图 1B为斜波滤波反投影算法重建的结果;图 1C为汉宁滤波反投影算法重建的结果;图 1D为非单调全变分最小化(NTVM)算法重建的结果;图 1E为本文提出的全广义变分最小化方法重建的结果。为了进一步展现本方法重建效果,图 2给出了对应图 1的局部放大图。由图 2可以清晰的看出本文方法对噪声和伪影的抑制效果。

|
图 1 Clock体模图像和不同方法重建的图像 Figure 1 Clock phantom and image reconstructed by different methods. A: Clock phantom; B: Image reconstructed by FBP algorithm with ramp filter; C: Image reconstructed by FBP algorithm with hanning filter; D: Image reconstructed by NTVM method; E: Image reconstructed by TGV method. |

|
图 2 Clock体膜图像局部放大图 Figure 2 Zoomed-in views of the Clock phantom and images reconstructed by different methods. Clock phantom (first column); Image reconstructed by FBP algorithm with ramp filter (second column); Image reconstructed by FBP algorithm with hanning filter (third column); Image reconstructed by NTVM method (fourth column); Image reconstructed by TGV method (fifth column). |
通过计算重建图像的信噪比和均方误差可以定量地分析不同方法的差异。信噪比计算公式为:
| $ SNR = 10{\log _{10}}\left( {\frac{{\sum\nolimits_i {{{\left( {{F_{rec}}\left( i \right) - {{\bar F}_{rec}}} \right)}^2}} }}{{\sum\nolimits_i {{{\left( {{F_{rec}}\left( i \right) - {F_{ture}}\left( i \right)} \right)}^2}} }}} \right) $ | (19) |
均方误差计算公式为:
| $ NMSE = \left( {\frac{{\sum\nolimits_i {{{\left( {{F_{rec}}\left( i \right) - {F_{ture}}\left( i \right)} \right)}^2}} }}{{\sum\nolimits_i {{{\left( {{F_{ture}}\left( i \right)} \right)}^2}} }}} \right) $ | (20) |
其中,Frec(i)表示像素点i通过算法得到的重建图像的灰度值,Frec表示重建图像Frec中所有像素点灰度的平均值;Fture(i)表示真实图像像素点i处的灰度值。
由表 1的性噪比和均方误差分析可以看出,相对于滤波反投影和非单调最小化方法,本文提出的重建图像的方法具有最高的信噪比和最小的均方误差。与NTVM算法相比,TGV方法信噪比提高了2.61%,而相应的均方误差减少了13.04%。
| 表 1 Clock体膜图像的信噪比和均方误差 Table 1 SNR and NMSE of the Clock phantom |
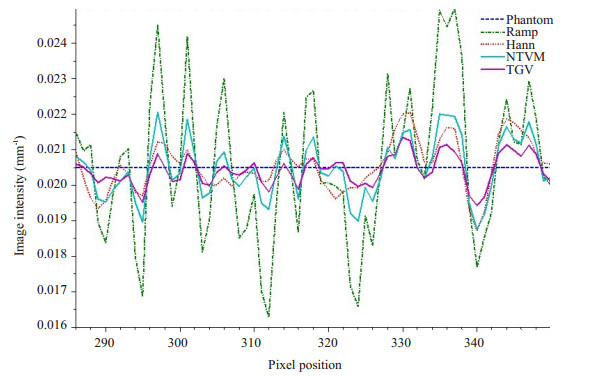
为了进一步验证本文提出方法的优越性,我们分别给出了4种方法重建结果的线剖面图(图 3),其中横坐标为图像像素位置,横坐标为图像的衰减值。由图 3可以看出本文提出的重建图像的方法与其他3种方法相比,能够较好的接近真实图像的线剖面。
|
图 3 Clock体膜图像的线剖面图 Figure 3 Profiles of the clock phantom. |
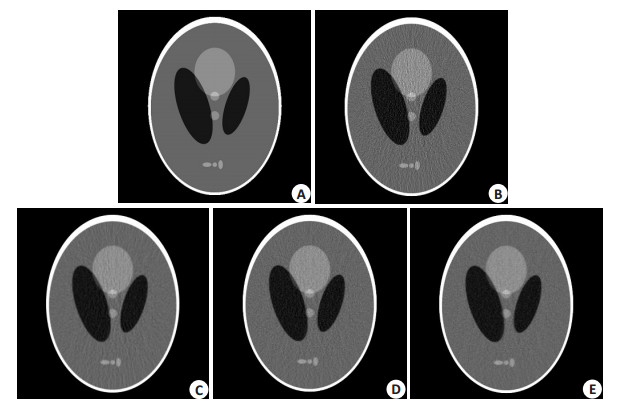
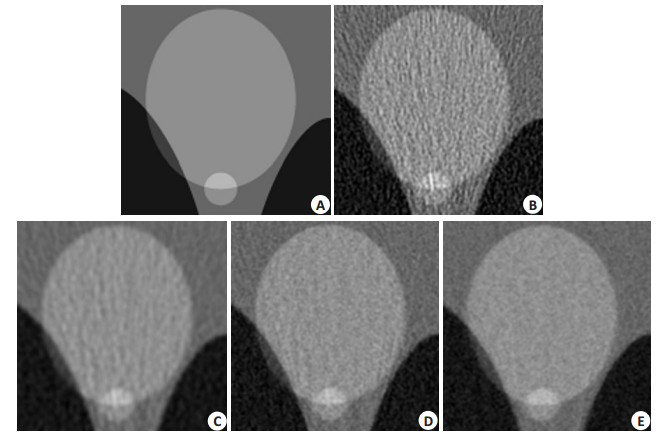
Shepp-Logan体模实验结果如图 4所示。其中,图 4A为真实的体模图像;图 4B为通过斜波滤波反投影算法重建的结果;图 4C为汉宁滤波反投影算法重建的结果;图 4D为非单调全变分最小化算法重建的结果;图 4E为本文提出的全广义变分方法重建的结果。图 5给出了低剂量CT重建结果的一个局部的放大图。
|
图 4 Shepp-Logan体模图像和不同方法重建的图像 Figure 4 Shepp-Logan phantom and images reconstructed by different methods. A: Clock phantom; B: Image reconstructed by FBP algorithm with ramp filter; C: Image reconstructed by FBP algorithm with hanning filter; D: Image reconstructed by NTVM method; E: Image reconstructed by TGV method. |
|
图 5 Shepp-Logan体膜图像局部放大图 Figure 5 Zoomed-in views of the Shepp-Logan phantom and images reconstructed by different methods. A: Clock phantom; B: Image reconstructed by FBP algorithm with ramp filter; C: Image reconstructed by FBP algorithm with hanning filter; D: Image reconstructed by NTVM method; E: Image reconstructed by TGV method (fifth column). |
由表 2的信噪比和均方误差分析可以看出,与其他3种方法相比,本文提出的全广义变分方法在提高图像重建的信噪比,降低重建图像均方误差方面均有上佳表现。与NTVM算法相比,TGV方法信噪比提高了1.03%,而相应的均方误差减少了8%。
| 表 2 Shepp-Logan体膜图像的信噪比和均方误差 Table 2 SNR and NMSE of the Shepp-Logan phantom |
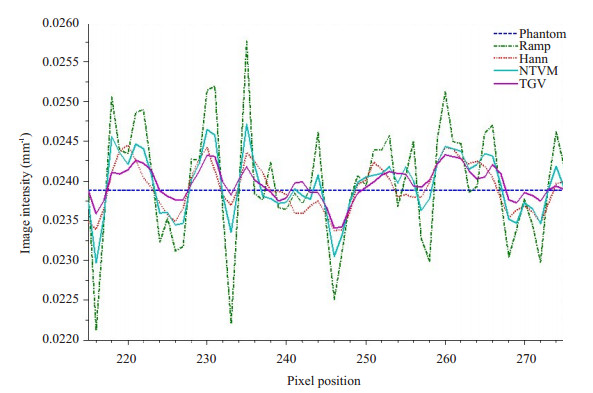
此外,为了更直观的验证重建图像的质量,我们画出了重建图像的线剖面图(图 6),其中横坐标为图像像素位置,横坐标为图像的衰减值。由线剖面图可以看出本文提出的方法重建的图像与真实图像的线剖面有更高的吻合度。
|
图 6 Shepp-Logan体膜图像的线剖面图 Figure 6 Profiles of the Shepp-Logan phantom. |
基于TV最小化的CT图像重建方法在抑制噪声和伪影方面取得了很好的效果。由于TV是基于图像分段常量的假设,当噪声水平非常高时,会产生严重的阶梯效应。针对TV方法重建的图像会产生阶梯效应的问题,本文提出了一个基于TGV正则化的低剂量CT重建算法,该方法不需要在投影数据满足分段常数假设。由于TGV利用了高阶导数信息,在不满足分段常量的假设下,本文方法可以有效去除噪声的同时,可以有效地抑制噪声与条形伪影。数值仿真实验结果表明本文提出的方法可以有效地抑制低剂量CT图像中的噪声和伪影,消除TV正常产生的阶梯效应,从而改善低剂量CT图像重建的质量。
在Clock体膜实验中,由图 1可以看出斜波滤波反投影和汉宁滤波反投影算法重建的图像含有大量的噪声和条形伪影,图像质量严重退化。非单调全变分算法重建的图像虽然在一定程度上减少了CT图像的条形伪影和噪声,但由于TV正则化的缺陷,部分伪影和噪声仍然存在。从视觉效果评价来看,我们提出的方法在去除图像的噪声和条形伪影方面具有更佳的表现。在Shepp-Logan体膜实验中,由图 4我们可以看到,相比滤波反投影和非单调全变分最小化方法,我们提出的全广义变分最小化方法在抑制噪声与条形伪影和保持边缘方面都有良好表现,可以更好的保持图像一致性。进一步,由体膜图像重建结果的放大图可以明显的看出,本文提出的全广义变分方法重建的图像对噪声和伪影有更好的抑制作用。此外,Clock和Shepp-Logan体膜实验的定量实验结果进一步表明,本文提出的方法比非单调全变分算法更具优越性。
由于本文提出的方法需要根据具体的重建目标人工选择正则化参数,大大限制了其更为广泛的应用。从国内外的研究现状来看,目前还没一种有效的参数选择方式,使得正则化的自适应参数调整达到最佳状态。因此,如何自适应选择正则化化参数是我们今后研究的一个重点课题。
| [1] | Einstein A, Henzlova M, rajagopalan S. estimating risk of cancer associated with radiation exposure from 64-slice CT coronary angiography[J]. J Am Med Assoc, 2007, 298(3): 317-23. DOI: 10.1001/jama.298.3.317. |
| [2] | Kopka L, Funke M, Breiter N, et al. An anatomically adapted variation of the tube current in CT. Studies on radiation dosage reduction and image quality[J]. Rofo, 1995, 163(6): 383-7. |
| [3] | Herzog C, Mulvihill DM, Nguyen SA, et al. Pediatric cardiovascular CT angiography: Radiation dose reduction using automatic anatomic tube current modulation[J]. AJR Am J Roentgenol, 2008, 190(5): 1232-40. DOI: 10.2214/AJR.07.3124. |
| [4] | Rudin LI, Osher S, Fatemi E. Nonlinear total variation based noise removal algorithms[J]. Physica D, 1992, 60(1/4): 259-68. |
| [5] | Wang J, Guan H, Solberg T. Inverse determination of the penalty parameter in penalized weighted least-squares algorithm for noise reduction of low-dose CBCT[J]. Med Phys, 2011, 38(7): 4066-72. DOI: 10.1118/1.3600696. |
| [6] | Niu S, Gao Y, Bian Z, et al. Sparse-view X-ray CT Reconstruction via total generalized variation regularization[J]. Phys Med Biol, 2014, 59(12): 2997-3017. DOI: 10.1088/0031-9155/59/12/2997. |
| [7] | 马建华, 陈武凡. 基于最大互信息量熵差分割的CT金属伪影消除[J]. 电子学报, 2009, 37(8): 1779-83. |
| [8] | 张善立, 张华, 胡德斌, 等. 基于边缘检测算子的Huber正则化阈值选择方法在低剂量CT重建中的应用[J]. 南方医科大学学报, 2015, 35(3): 375-9. |
| [9] | Niu S, Huang J, Bian Z, et al. Iterative Reconstruction for sparse-view X-ray CT using alpha-divergence constrained total generalized variation minimization[J]. J Xray Sci Technol, 2017, 25(4): 673-88. |
| [10] | Zhang Y, Ma J, Iyengar P, et al. A new CT Reconstruction technique using adaptive deformation recovery and intensity correction (ADRIC)[J]. Med Phys, 2017, 44(6): 2223-41. DOI: 10.1002/mp.2017.44.issue-6. |
| [11] | Gao Y, Bian Z, Huang J, et al. Low-dose X-ray computed tomography image Reconstruction with a combined low-mAs and sparse-view protocol[J]. Opt Express, 2014, 22(12): 15190-210. DOI: 10.1364/OE.22.015190. |
| [12] | Huang J ZY, Chen WF. Iterative image Reconstruction for sparseview CT using normal-dose image induced total variation prior[J]. PLoS One, 2013, 8(11): e79709. DOI: 10.1371/journal.pone.0079709. |
| [13] | Li J, Niu S, Huang J, et al. An efficient augmented lagrangian method for statistical X-Ray CT image reconstruction[J]. PLoS One, 2015, 10(10): e0140579. DOI: 10.1371/journal.pone.0140579. |
| [14] | Li TF, Xiang L, Jing W, et al. Nonlinear sinogram smoothing for low-dose X-ray CT[J]. IEEE Trans Nucl Sci, 2004, 51(5): 2505-13. DOI: 10.1109/TNS.2004.834824. |
| [15] | Huang J, Ma J, Liu N, et al. Sparse angular CT Reconstruction using non-local means based iterative-correction POCS[J]. Comput Biol Med, 2011, 41(4): 195-205. DOI: 10.1016/j.compbiomed.2011.01.009. |
| [16] | Wang J, Li TF. Lu H B and liang Z G, penalized weighted leastsquares approach to sinogram noise reduction and image Reconstruction for low-dose x-ray computed tomography[J]. IEEE Trans Med Imaging, 2006, 25(10): 1272-83. DOI: 10.1109/TMI.2006.882141. |
| [17] | Sonka M, Fitzpatrick JM. Handbook of medical imaging[M]. SPIE, Bellingham, Washington: 2000: 1-70. |
| [18] | Wang J, Li T, Xing L. Iterative image Reconstruction for CBCT using edge-preserving prior[J]. Med Phys, 2009, 36(1): 252-60. |
| [19] | Wang J, Liang Z, Lu H. Multiscale penalized weighted leastsquares sinogram restoration for low-dose X-ray computed tomography[J]. Conf Proc IEEE Eng Med Biol Soc, 2006, 1(3): 3282-5. |
| [20] | Wang J, Li T, Lu H, et al. Noise reduction for Low-Dose SingleSlice helical CT sinograms[J]. IEEE Trans Nucl Sci, 2006, 53(3): 1230-7. DOI: 10.1109/TNS.2006.874955. |
| [21] | Xu JY, Taguchi K, Tsui B M. statistical projection completion in x-ray CT using consistency conditions[J]. IEEE Trans Med Imaging,, 2010, 29(8): 1528-40. DOI: 10.1109/TMI.2010.2048335. |
| [22] | Bian Z, Ma J, Huang J, et al. SR-NLM: a sinogram restoration induced non-local means image filtering for low-dose computed tomography[J]. Comput Med Imaging Graph, 2013, 37(4): 293-303. DOI: 10.1016/j.compmedimag.2013.05.004. |
| [23] | Tang J., Nett B, Chen G. Performance comparison between total variation(TV)-based compressed sensing and statistical iterative Reconstruction algorithms[J]. Phys Med Biol, 2009, 54(19): 5781-804. DOI: 10.1088/0031-9155/54/19/008. |
| [24] | Yu GH, Qi LQ, Dai YH. On nonmonotonechambolle gradient projection algorithms for total variation image restoration[J]. J Mathemat Imaging and Vision, 2009, 35(2): 143-54. DOI: 10.1007/s10851-009-0160-3. |
| [25] | Makitalo M, Foi A. On the inversion of the anscombe transformation in low-count poisson image denoising[C] //LNLA: 2009 International Workshop on Local and Non-local Approximation in Image Processing, 2009: 26-32. |
| [26] | Anscombe FJ. The transformation of poisson, binomial and negative-binomial data[J]. Biometrika, 1948, 35(3/4): 246-54. DOI: 10.2307/2332343. |
| [27] | Bredies K, Dong Y, Hintermuller M. Spatially dependent regularization parameter selection in total generalized variation models for image restoration[J]. Int J Comput Math, 2013, 90(1): 109-23. DOI: 10.1080/00207160.2012.700400. |
| [28] | 钱珊珊, 黄静. 基于投影数据非单调性全变分恢复的低剂量CT重建[J]. 电子学报, 2011, 39(7): 1702-7. |
| [29] | Knoll F1, Bredies K, Pock T, et al. Second order total generalized variation(TGV)for MRI[J]. Magn Reson Med, 2011, 65(2): 480-91. DOI: 10.1002/mrm.22595. |
| [30] | Chambolle A, Pock T. A First-Order Primal-Dual algorithm for convex problems with applications to imaging[J]. J Math Imaging Vis, 2011, 40(1): 120-45. DOI: 10.1007/s10851-010-0251-1. |
 2017, Vol. 37
2017, Vol. 37

