无创测定局部心肌血流量(RMBF)一直是临床心脏学所追求的目标之一[1-3]。通过从动态图像中估计血输入函数与输出函数[4-5],并应用动力学模型,可以得到绝对的定量参数(如物质转运速率、代谢速度和受体结合率等功能参数等),从而实现对心肌血流的定量分析[6-8]。在动力学模型的应用中,血输入函数的估计是非常关键的,结果的准确与否直接影响到后期的定量分析,目前广泛采用的估计血输入函数方法为基于感兴趣区域法,该方法简单易行,但极度依赖于医生手工勾画的感兴趣区域,而感兴趣区域的准确性又受医生个人经验及部分容积效应影响。因子分析作为从变量群中提取公共因子的统计技术[9],已经被用来从动态图像中无创地提取血输入函数和组织的时间活度曲线[10-11],如基于主成分分析[12-15]、独立成分分析[16-17]、最小二乘法[6, 15]、最大似然法[18]的因子分析模型相继被提出。然而,用因子分析方法获得的结果存在非唯一性,各种基于先验信息的方法被提出用来解决结果的非唯一性[18-20],另外,Sitek等[19]提出基于最小化各因子图像间的重叠程度的优化方法可以获得唯一的结果。
合理地构建因子模型与实际数据之间的测度是精确建模的关键,目前在因子分析模型中常见的是基于高斯噪声模型的最小二乘测度与基于泊松噪声模型的最大似然测度[6, 18, 21]。而临床获取动态PET图像噪声很难直接用高斯或泊松模型进行刻画,因此,本文提出基于α散度的因子分模型,α散度由S.Amari提出,是诸多信息散度族中的一种,通过选取不同的α值,可以用于任意噪声模型的数据测度[22-23]。
针对因子分析模型中解的非唯一性,传统上利用最小化因子图像间的重叠程度这一约束来解决该问题,但由于受到PET图像分辨率和部分容积效应的影响,心肌信号经常会掺杂着10%~15%的血液信号,基于最小化因子图像之间的重叠程度的约束未能考虑到这一事实。在动态PET研究中,每一个像素的时间行为可以通过曲线时间活力(TAC)来描述,我们将具有相同时间行为的像素进行聚类[24],把这一聚类结果作为先验约束用来解决因子分析模型中的非唯一性,得到具有生理意义的组织活度曲线。因子分析模型应用于基于XCAT (Extended Cardiac-Torso phantom)体模[25]仿真的82Rb PET心肌灌注仿真数据中,实验均表明我们的方法在视觉评价及量化评价等方面优于传统的因子分析模型。
1 方法 1.1 PET图像的获取对于动态序列PET图像I,像素点j在第m帧的示踪剂活度xjm可通过以下积分式计算得到[26]:
| $ {x_{jm}} = \int_{{t_{m,s}}}^{{t_{m,e}}} {c\left( {j,t} \right){e^{ - \lambda \tau }}{\rm{d}}t} $ | (1) |
其中,c(j,t)表示像素点在时间点t的示踪剂活度,tm, s和tm, e分别表示第m帧的起始时间和终止时间。那么
| $ I = \left( {\begin{array}{*{20}{c}} {{x_{11}}}&{{x_{12}}}& \cdots &{{x_{1{n_m}}}}\\ {{x_{21}}}&{{x_{22}}}& \cdots &{{x_{2{n_m}}}}\\ \vdots&\vdots&\ddots&\vdots \\ {{x_{{n_j}1}}}&{{x_{{n_j}2}}}& \cdots &{{x_{{n_j}{n_m}}}} \end{array}} \right) $ | (2) |
其中I ∈ Rnj × nm,I的一列表示一帧图像,I的一行表示单个像素点的时间活度曲线。
动态PET序列图像可分解为有限的时间序列向量F和与其相对应体素的空间分布C,这一分解模型可用下式来表示
| $ I = CF + \varepsilon $ | (3) |
其中动态PET图像I的大小为N×T,其中N表示每一帧PET图像的像素点数目,T表示动态图像的帧数。因子矩阵F的大小为K×T,因子图像C的大小为N×K,其中K为所需提取的因子数目。ε表示剩余信号,即图像的噪声和被模型所忽略的小部分信号。在这里,为保证模型的实际应用价值,因子数目K要满足K≪N,K≪T。
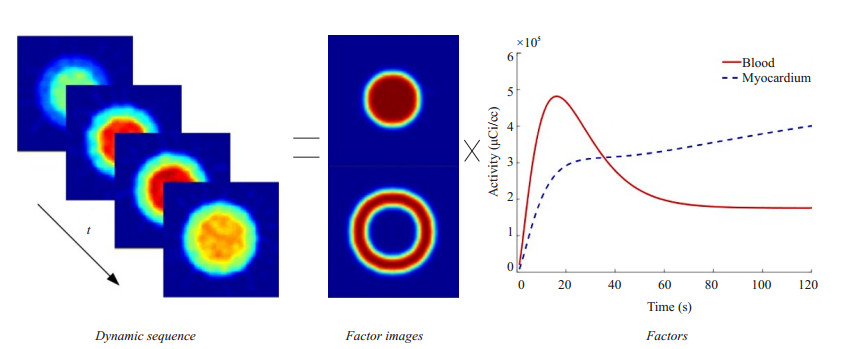
图 1表示对动态序列PET图像做因子分析的示意图,在理想状况下,因子矩阵F对应于动态图像中各个生理组织的时间活度曲线,因子图像C对应于各个生理组织的空间分布。
|
图 1 对动态序列做因子分析示意图 Figure 1 A schematic illustration of factor analysis for dynamic sequences. |
因子分析模型的求解主要由两个步骤来完成:(1)通过最小化模型与真实图像之间的测度来分解图像,得到初始的因子与因子图像。(2)解决模型中的非唯一问题。
我们通过α散度来测定图像I与模型CF之间的偏差,α散度由S.Amari提出,是诸多信息散度族中的一种,用于测量两个数据分布p(x)和q(x)之间的偏差,其定义为:
| $ {D_\alpha }\left( {p,q} \right) = \frac{1}{{\alpha \left( {1 - \alpha } \right)}}\sum\limits_i {\left( {\alpha {p_i} + \left( {1 - \alpha } \right){q_i} - p_i^\alpha q_i^{1 - \alpha }} \right)} ,\alpha \in R $ | (4) |
结合信息散度的特点,本文提出最小化基于α散度测度的目标函数来估计因子F与因子图像C:
| $ {f_\alpha }\left( {C,F} \right) = \frac{1}{{\alpha \left( {1 - \alpha } \right)}}\sum\limits_i {\sum\limits_f {\left( \begin{array}{l} \alpha {I_{if}} + \left( {1 - \alpha } \right){\left( {CF} \right)_{if}}\\ - I_{if}^\alpha \left( {CF} \right)_{if}^{1 - \alpha } \end{array} \right)} } ,\alpha \in R $ | (5) |
基于α散度的动态PET图像的因子分析模型可表示为以下凸优化问题:
| $ \left( {C,F} \right) = \mathop {\arg \min }\limits_{{C_{ik}} \ge 0,{F_{kf}} \ge 0} {f_\alpha }\left( {C,F} \right) $ | (6) |
我们采用一种迭代的方式去解决上式,具体算法如下:
ⅰ.初始化C,F:设置C中元素为0-1之间的随机数,再根据C估计初始F;
ⅱ.迭代:
(a) C-step:根据当前的动态图像I和F估计C;
(b) 将C中的小于零的元素置为0:;
(c) F-step:根据当前的动态图像I和C估计F;
(d) 将F中的小于零的元素置为0:;
(e) 检查是否收敛,若不收敛,则返回步骤a;
ⅲ.归一化因子图像C,再根据缩放的比例缩放F;
其中,在C-step中,令
| $ C_{m + 1}^\alpha = \frac{{C_m^\alpha \sum\limits_{i,f} {{F_{kf}}{{\left( {\frac{{{I_{if}}}}{{{{\left( {F{C_m}} \right)}_{if}}}}} \right)}^\alpha }} }}{{\sum\limits_f {{F_{kf}}} }}; $ |
在F-step中,令
| $ F_{m + 1}^\alpha = \frac{{F_m^\alpha \sum\limits_{i,f} {{C_{ik}}{{\left( {\frac{{{I_{if}}}}{{{{\left( {C{F_m}} \right)}_{if}}}}} \right)}^\alpha }} }}{{\sum\limits_i {{C_{ik}}} }} $ |
容易发现,式1描述的因子模型的结果在数学上并不是唯一的[27],因子和因子图像的非唯一性可以通过下式说明
| $ I = \left( {CR} \right)\left( {{R^{ - 1}}F} \right) = C'F' $ | (7) |
其中,C和F表示真实的因子图像矩阵和因子矩阵,通过一个可逆的矩阵R,理论上能得到无数组符合模型描述的因子图像C'和F'。因此,我们必须找到合理的约束条件确保结果的唯一性。
A.传统方法:最小化因子图像之间的重叠程度约束
sitek.A假设因子图像之间的重叠程度最小(MSO, minimal structure overlap)的作为唯一性约束条件,因子间重叠程度的计算公式为
| $ {f_{uni}}\left( R \right) = \sum\limits_{p = 1}^P {\sum\limits_{q = p + 1}^P {\sum\limits_{i = 1}^N {\frac{{{{\left| {CR} \right|}_{ip}}}}{{\sqrt {\sum\limits_{i = 1}^N {\left( {CR} \right)_{ip}^2} } }}\frac{{{{\left| {CR} \right|}_{iq}}}}{{\sqrt {\sum\limits_{i = 1}^N {\left( {CR} \right)_{iq}^2} } }}} } } $ | (8) |
惩罚项fn(CR, R-1F)保证因子和因子图像的值为非负,可用下式表示:
| $ \begin{array}{l} {f_n}\left( R \right) = \sum\limits_{i = 1}^K {\sum\limits_{k = 1}^K {H\left( {{{\left( {CR} \right)}_{ik}}} \right)} } + \sum\limits_{f = 1}^T {\sum\limits_{k = 1}^K {H\left( {{{\left( {{R^{ - 1}}F} \right)}_{kf}}} \right)} } ,\\ 其中\;H\left( x \right) = \left\{ \begin{array}{l} 0,\;\;\;\;x \ge 0\\ {x^2},\;\;x < 0 \end{array} \right. \end{array} $ | (9) |
最小化目标函数(funi+b1fn),求得R的最优解,并获得最终的因子图像(CR)和代表每个组织活度曲线(R-1F)的具有实际生理意义的因子。
B.新方法:基于动力学聚类的约束
由于受到PET图像分辨率和部分容积效应的影响,心肌信号经常会掺杂着10%~15%的血液信号,最小化因子图像之间的重叠程度约束未能考虑到这一事实。因此,本文提出一种基于动力学的时间活度曲线聚类(KB, Kinetic Based)的先验约束来解决因子分析模型中的非唯一问题。
在动态PET研究中,每一个像素的时间行为可以通过TAC曲线来描述,因此,我们基于像素的动力学对图像进行分类。我们的目标是通过动态序列图像的TAC曲线的形状和级数对图像进行分类,使得像素TAC在同一类是同质的,而不同类之间是异质的。假设动态图像I具有K个不同特征的类,模糊C均值聚类算法基于最小化目标函数
| $ J = \sum\limits_{j = 1}^{{n_j}} {\sum\limits_{k = 1}^K {u_{kj}^q{{\left\| {{I_j} - {v_k}} \right\|}^2}} } $ | (10) |
其中||·||代表欧氏距离,Ij表示图像I中第j个像素的TAC曲线,vk是第k个聚类的中心的TAC,ukj表示第j个像素属于第k类的隶属度,q(q>1)是模糊参数。
目标函数的解可以通过如下迭代式得到:
ⅰ.设置初始的类数K和停止准则ε;
ⅱ.随机初始化模糊隶属度矩阵U(0)包含每一个单独ukj(0)值;
ⅲ.设置循环初始值b=0;
ⅳ.由U(b)计算聚类中心vk(b);
| $ v_k^{\left( b \right)} = \frac{{\sum\limits_j {{{\left( {u_{kj}^{\left( b \right)}} \right)}^q}{I_j}} }}{{\sum\limits_j {{{\left( {u_{kj}^{\left( b \right)}} \right)}^q}} }} $ |
ⅴ.计算隶属度矩阵U(b+1)
| $ u_{kj}^{\left( {b + 1} \right)} = 1/\sum\limits_{i = 1}^K {{{\left( {\frac{{\left\| {{I_j} - {v_k}} \right\|_w^2}}{{\left\| {{I_j} - {v_i}} \right\|_w^2}}} \right)}^{1/\left( {q - 1} \right)}}} $ |
ⅵ.如果max{U(b) -U(b + 1)}<ε则停止;否则,设b=b+ 1返回第ⅳ步。
将聚类中心vk通过式(11)作为像素动力学先验信息应用到因子分析唯一性约束当中,
| $ {f_{TAC}}\left( R \right) = \sum\limits_{k = 1}^K {{{\left\| {{{\left( {{R^{ - 1}}F} \right)}_k} - {v_k}} \right\|}_1}} $ | (11) |
通过最小化目标函数(fTAC+b2fn)来解决因子分析中的非唯一问题,求得R的最优解,最终获得因子图像(CR)和代表每个组织活度曲线(R-1F)的具有实际生理意义的因子。
2 实验(1) 计算机仿真数据
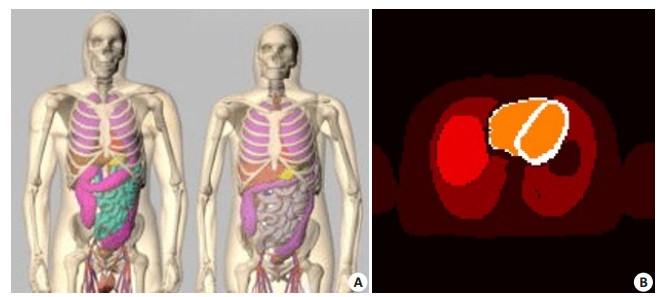
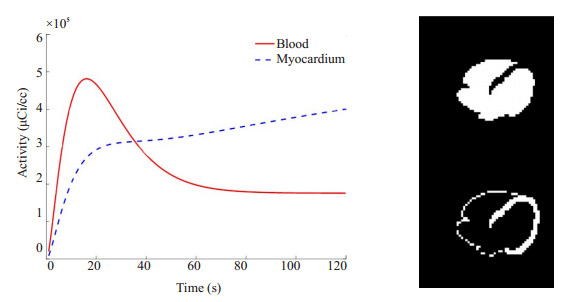
在计算机仿真实验中,本文使用基于如图 2所示的XCAT数字体膜,心脏区域由血池,心肌组织两个部分构成,在这里将心脏区域单独分离出来。模型的体素点个数为64×64×30,体素点尺寸大小为3.27 mm×3.27 mm× 3.27 mm。我们基于单房室模型[28]模拟心脏区域生理代谢的功能成像过程,使用的放射性核素为82Rb,半衰期为1.27 min。仿真过程中,血输入函数以及各组织对应的动力学参数的测量值均来自美国约翰霍普金斯大学PET医学中心的5位志愿者[26]。基于单房室模型、血输入函数以及相应的动力学参数(设置动力学参数K1= 1.4822 mL/min/g,k2=0.3159/min及血体积分数为Vp= 0.3829)生成心肌组织的时间活度曲线,各组织时间活度曲线及空间分布如图 3所示。整个动态PET扫描协议设置为:12×5 s,6×10 s共计18个时间帧。将每一帧血池与心肌组织的时间活度赋值到其对应组织的空间分布位置上,生成模拟心脏区域的动态PET图像。
|
图 2 (A) 4D XCAT数字体膜的正位像(左:男性,右:女性)及(B)女性心脏区域水平切片 Figure 2 Anterior views of the 4D XCAT digital phantom (A; left: male, right: female) and the female horizontal plane of myocardial region (B). |
|
图 3 血池与心肌组织的时间活度曲线及空间分布位置(横截面第14层) Figure 3 Time-activity curve and spatial distribution position of blood pool and myocardial tissue (14th slice of the horizontal plane). |
将动态图像进行正向投影得到随时间变化的无噪投影数据。投影数据仿真过程中产生的总光子计数设置为5×106。在投影数据中加入泊松噪声便可得到仿真的加噪投影数据。本文采用FBP重建算法对加噪的投影数据进行重建。得到重建图像之后,用FWHM=4 mm的高斯滤波器对重建出的动态图像进行去噪。本研究仿真实验均基于该仿真数据。
(2) 对照方法及评价指标
在模型的求解中的第一步中,引入了α散度作为测度量化模型与真值图像之间的距离,我们将其与传统的最小二乘测度进行比较。本文采用归一化误差δ1评价不同测度在每一帧的剩余信号ε,用归一化误差δ2评价不同测度评价所有帧的剩余信号ε。
| $ \begin{array}{l} {\delta _1} = \frac{{\sqrt {\frac{1}{N}\sum\limits_{i = 1}^N {{{\left( {{I_{if}} - {{\left( {CF} \right)}_{if}}} \right)}^2}} } }}{{\frac{1}{N}\sum\limits_{i = 1}^N {{I_{if}}} }},\\ {\delta _2} = \frac{{\sqrt {\frac{1}{{N \cdot T}}\sum\limits_{f = 1}^T {\sum\limits_{i = 1}^N {{{\left( {{I_{if}} - {{\left( {CF} \right)}_{if}}} \right)}^2}} } } }}{{\frac{1}{{N \cdot T}}\sum\limits_{f = 1}^T {\sum\limits_{i = 1}^N {{I_{if}}} } }} \end{array} $ | (12) |
为了验证本文中动力学聚类在解决非唯一性问题的准确性,我们将基于动力学聚类约束的因子分析模型与传统的最小化因子间重叠程度(MSO)的模型进行比较。除了视觉评价外,采用量化指标RMSE对因子与仿真的组织活度曲线分布进行比较:
| $ RMSE = \frac{{\sum\limits_f {W \cdot \left| {norm\left( F \right) - norm\left( {{F_{ref}}} \right)} \right|} }}{{\sum\limits_f {W \cdot norm\left( {{F_{ref}}} \right)} }} \times 100\% $ | (13) |
其中F代表因子曲线,Fref代表各组织的活度曲线。W代表每一帧的时间间隔,norm(F)代表将F进行归一化,即norm(F) =
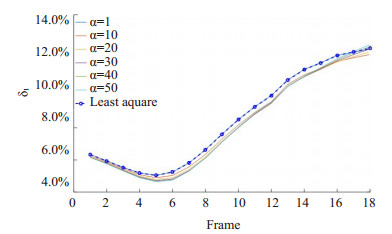
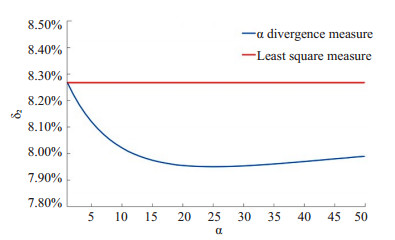
通过最小化模型与真实图像之间的测度得到初始因子和因子图像后,可用剩余信号来评价不同测度的优劣。图 4是最小二乘测度与α散度测度(α=1,10,20,30,40,50)所得出的模型归一化误差δ1,图 5是动态图像所有帧的归一化误差δ2随α的变化情况,由图可知,仅当α= 1时α测度与最小二乘测度的归一化误差相等,当α取其它值时,α散度测度的结果的归一化误差均优于最小二乘测度。
|
图 4 不同测度下模型在每帧的归一化误差δ1 Figure 4 Normalization error δ1 of the model in each frame under different measures. |
|
图 5 不同测度下模型的归一化误差δ2 Figure 5 Normalization error δ2 of the model under different measures. |
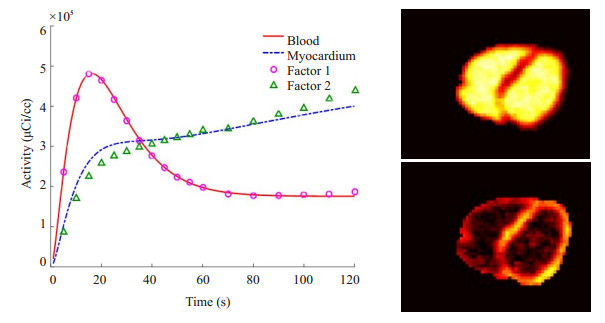
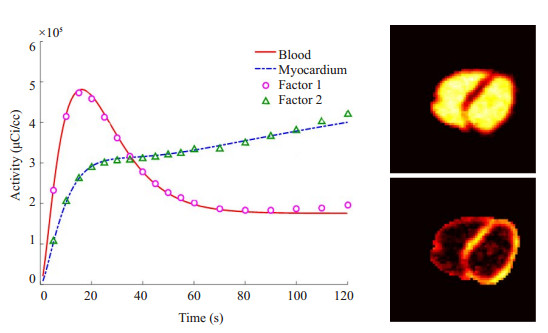
得到初始因子后,用最小化因子间重叠程度(MSO)和基于动力学聚类(KB)的两种约束方法解决因子分析模型中的非唯一问题。图 6、图 7分别给出了对我也燥比(SNR) =10的动态序列用两种不同约束方法(模型的测度为α散度测度,且α=25)所得到的因子和因子图像,由图可知,所得出的因子1与因子2分别对应于血池TAC与心肌TAC,所得到的因子图像1与因子图像2 (图中绘制的是第14层横断面图)也对应于心脏的血池和心肌组织,对于血池的活度曲线,两种方法所得到的因子的精确程度无显著差别,而对于心肌活度曲线,用KB约束得到的因子比MSO约束得到的因子精确度高。
|
图 6 用MSO约束所得因子及因子图像 Figure 6 The factors and factor images obtained by MSO constraints. |
|
图 7 用KB约束所得因子及因子图像 Figure 7 Factors and factor images obtained by KB constraints. |
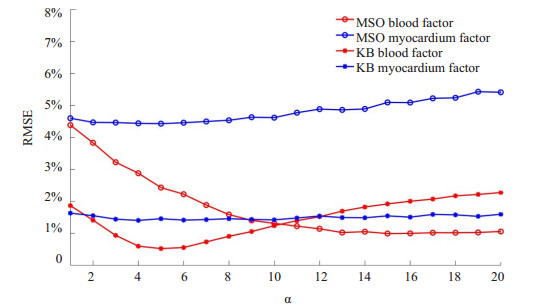
为了进一步验证α散度在本模型中的有效性基选取最优的α值,本文选取不同的α值在两种约束模型下进行因子分析,为避免实验受噪声的随机性影响,针对每种方法运行30次求平均值,绘制出不同α值在MSO和KB两种约束下各因子的RMSE图 8,在KB约束中,心肌因子的RMSE基本保持稳定,当α=5时估计的血池因子RMSE最小,因此选取5作为本文的最优的α值;而在MSO约束中,两因子在α>12时基本趋于稳定。选取了最优的值后,将α散度测度与最小二乘测度在两种不同约束下作比较见表 1,结果说明α散度的RMSE比最小二乘的低,即该测度更能提取出更准确的结果。此外,由图 8可知无论α取何值,用KB约束模型得出的两因子的平均RMSE曲线位于MSO的下方,这亦说明了动力学聚类约束要优于小化因子间重叠程度约束。
|
图 8 不同α值在MSO和KB两种约束下各因子的RMSE Figure 8 RMSE of the obtained factors with MSO constraints and KB constraints underα divergence measure. |
| 表 1 两种测度下应用MSO约束和KB约束的所得各因子的RMSE Table 1 MSE of the obtained factors with MSO constraints and KB constraints under two measures |
为了评价噪声对模型的影响,我们通过在图像的投影域中加入不同规模的噪声,重建出不同信噪比的图像。表 2表示对不同信噪比的动态序列,用MSO和KB两种不同约束所得到的各因子的RMSE。由表可知,当噪声逐渐增大时,因子的RMSE也相应增大,估计的血池的时间活度曲线比心肌活度曲线精确。
| 表 2 不同信噪比下各因子的RMSE Table 2 RMSE of various factors under different SNRs |
α散度测度的目的是将动态图像做一个初步的分解,由于分解的结果具有非唯一性,所以根据聚类中心作为先验信息将其中一组解线性变换为具有实际生理意义的时间活度曲线。值得注意的是,动力学聚类结果不能作为最终的TAC,因为聚类与聚类中心过于粗糙,不能较精确地反应真实的动态图像,尤其是对于噪声较大的动态图像。
在加入唯一性约束时,我们引入一个惩罚项fn来保证我们得到的结果是非负的,对于两个正则化参数b1和b2,实验发现当b1,b2∈ [10, 500]时,结果无明显差异,鉴于此在本实验中将b1,b2均设置为100。对于不同的数据,我们可以参考本数据选取合适的b值,若结果出现负值,我们只需要适当地增加b的值保证结果是非负的即可。
从该心脏体膜中提取的结果我们我发现,在同样规模噪声的情况下,估计出的血池的时间活度曲线比心肌组织的活度曲线要精确,主要原因是血池的体素数比心肌体素数多,受部分容积效应及噪声的影响较小。在心肌壁的某些部分仅有2~3个体素的厚度,极容易受到部分容积效应及噪声的影响降低结果的精确度。
本研究提出一种基于动力学聚类与α散度测度的动态三维心脏PET图像因子分析研究模型,实现了对心脏PET图像各组织的时间活度曲线进行精确提取。传统的因子分析模型利用最小二乘模型,用最小化因子图像间重叠程度来解决因子分析模型中的非唯一性问题,本文通过最小化动态图像与因子分析模型的α散度测度,可以通过不同的α值选取比最小二乘适合的测度得到初始因子及因子图像,并在旋转因子时引入PET图像像素的动力学聚类先验信息,我们将模型应用于基于XCAT的仿真数据上,通过实验分析发现,用α散度测度以及基于动力学聚类的先验约束均对组织活度曲线的提取的准确性有积极的作用,在高噪声下(SNR=5)仍能准确的提取出各组织的时间活度曲线,用视觉评价及量化评价等方法优势明显。然而,本方法在旋转因子时引入正则化参数无法自适应选择,在下一步工作中将进一步研究正则化参数自适应选择问题。
| [1] | 王荣福. PET/CT:分子影像学新技术应用[M]. 北京: 北京大学医学出版社, 2011: 108-13. |
| [2] | Su Y, Arbelaez AM, Benzinger TLS, et al. Noninvasive estimation of the arterial input function in positron emission tomography imaging of cerebral blood flow[J]. J Cereb Blood Flow Metab, 2013, 33(1): 115-21. DOI: 10.1038/jcbfm.2012.143. |
| [3] | Schupbach WMM, Emese B, Loretan P, et al. Non-invasive diagnosis of coronary artery disease using cardiogoniometry performed at rest[J]. Swiss Med. Wkly, 2008, 138(15-16): 230-8. |
| [4] | Bisker J. Principles and practice of positron emission tomography[J]. Am J Roentgenol, 2012, 180(5): 1238. |
| [5] | Garbarino S, Caviglia G, Brignone M, et al. Compartmental analysis of renal physiology using nuclear medicine data and statistical optimization[J]. Physics, 2012, 3(24): 625-37. |
| [6] | Fakhri GE, Sitek A, Guerin B, et al. Quantitative dynamic cardiac 82Rb PET using generalized factor and compartment analyses[J]. J Nucl Med, 2005, 46(8): 1264-71. |
| [7] | Moody J, Lee BC, Corbett JR, et al. Precision and accuracy of clinical quantification of myocardial blood flow by dynamic PET: A technical perspective[J]. J Nucl Cardiol, 2015, 22(5): 935-51. DOI: 10.1007/s12350-015-0100-0. |
| [8] | Tio RA, Dabeshlim A, Siebelink HM, et al. Comparison between the prognostic value of left ventricular function and myocardial perfusion reserve in patients with ischemic heart disease[J]. J Nucl Med, 2009, 50(2): 214-9. DOI: 10.2967/jnumed.108.054395. |
| [9] | Dehak N, Kenny PJ, Dehak R, et al. Front-end factor analysis for speaker verification[J]. IEEE Trans Speech Audi P, 2011, 19(4): 788-98. DOI: 10.1109/TASL.2010.2064307. |
| [10] | Kim J, Herrero P, Sharp T, et al. Minimally invasive method of determining blood input function from PET images in rodents[J]. J Nucl Med, 2006, 47(2): 330-6. |
| [11] | Klein R, Beanlands RS, Wassenaar RW, et al. Kinetic model-based factor analysis of dynamic sequences for 82-rubidium cardiac positron emission tomography[J]. Med Phys, 2010, 37(8): 3995-4010. DOI: 10.1118/1.3438474. |
| [12] | Ketata I, Sallemi L, Morainnicolier F, et al. Factor analysis-based approach for early uptake automatic quantification of breast cancer by 18F-FDG PET images sequence[J]. Biomed Signal Proces, 2014: 19-31. |
| [13] | Paola RD, Bazin JP, Aubry F, et al. Handling of dynamic sequences in nuclear medicine[J]. IEEE Trans Nucl Sci, 1982, 29(4): 1310-21. DOI: 10.1109/TNS.1982.4332188. |
| [14] | Wu HM, Hoh CK, Choi Y, et al. Factor analysis for extraction of blood time-activity curves in dynamic FDG-PET studies[J]. J Nucl Med, 1995, 36(9): 1714-22. |
| [15] | Whittle P. On principal components and least square methods of factor analysis[J]. Scand Actuar J, 2012, 35(3-4): 223-39. |
| [16] | Lord S, Galna B, Verghese J, et al. Independent domains of gait in older adults and associated motor and nonmotor attributes: validation of a factor analysis approach[J]. J Gerontol Ser A, 2013, 68(7): 820-7. DOI: 10.1093/gerona/gls255. |
| [17] | Mabrouk R, Dubeau F, Bentabet L. Dynamic cardiac PET imaging: extraction of time-activity curves using ICA and a generalized Gaussian distribution model[J]. IEEE Trans Biomed Eng, 2013, 60(1): 63-71. DOI: 10.1109/TBME.2012.2221463. |
| [18] | Su Y, Welch M J, Shoghi K, et al. The application of maximum likelihood factor analysis (MLFA) with uniqueness constraints on dynamic cardiac microPET data[J]. Phys Med Biol, 2007, 52(8): 2313-34. DOI: 10.1088/0031-9155/52/8/018. |
| [19] | Sitek A, Gullberg GT, Huesman RH. Correction for ambiguous solutions in factor analysis using a penalized least squares objective[J]. IEEE Trans Med Imaging, 2002, 21(3): 216-25. DOI: 10.1109/42.996340. |
| [20] | Boutchko R, Mitra D, Baker SL, et al. Clustering-initiated factor analysis application for tissue classification in dynamic brain positron emission tomography[J]. J Cereb Blood Flow Metab, 2015, 35(7): 1104-11. DOI: 10.1038/jcbfm.2015.69. |
| [21] | Jia S, Qian Y. Constrained nonnegative matrix factorization for hyperspectral unmixing[J]. IEEE Trans Geosci Electron, 2009, 47(1): 161-73. |
| [22] | Critchley F, Marriott P. Computing with Fisher geodesics and extended exponential families[J]. Stat Comput, 2014, 26(1): 1-8. |
| [23] | Teng Y, Zhang T. Generalized EM-type reconstruction algorithms for emission tomography[J]. IEEE Trans Med Imaging, 2012, 31(9): 1724-33. DOI: 10.1109/TMI.2012.2197758. |
| [24] | Lu L, Karakatsanis NA, Tang J, et al. 3.5D dynamic PET image reconstruction incorporating kinetics-based clusters[J]. Phys Med Biol, 2012, 57(15): 5035-55. DOI: 10.1088/0031-9155/57/15/5035. |
| [25] | Segars WP, Mahesh M, Beck TJ, et al. Realistic CT simulation using the 4D XCAT phantom[J]. Med Phys, 2008, 35(8): 3800-8. DOI: 10.1118/1.2955743. |
| [26] | 马晓勉, 路利军, 高园园, 等. 基于低秩框架的心肌灌注动态PET图像恢复[J]. 暨南大学学报:自然科学与医学版, 2016, 37(1): 78-86. |
| [27] | El Fakhri G, Trott CM, Sitek A, et al. Dual-tracer PET using generalized factor analysis of dynamic sequences[J]. Mol Imaging Biol, 2013, 15(6): 666-74. DOI: 10.1007/s11307-013-0631-1. |
| [28] | Watabe H, Ikoma Y, Kimura Y, et al. PET kinetic analysis--compartmental model[J]. Ann Nucl Med, 2006, 20(9): 583-8. DOI: 10.1007/BF02984655. |
 2017, Vol. 37
2017, Vol. 37

