超声成像是利用超声波在组织传播过程中的回波信号进行成像。在超声波传播过程中,由于人体软组织声阻抗的不均匀性和空间分布的随机性,形成了大量随机分布的散射粒子,其散射波在传播过程中由于相干干涉和相消干涉而形成超声图像中亮暗不定的斑点模式[1]。斑点统计分布特性与人体脏器组织中散射粒子的数量、散射强度等密切相关,与人体脏器组织解剖结构特征直接关联。故斑点的物理特征反映组织的结构特征。依据人体组织中每分辨单元内散射粒子数量和粒子散射性质,超声斑点分为4种类型:完全成熟型、完全解决型、部分成熟型和部分解决型[2-3]。完全成熟型是超声成像中最常见的斑点模型,反映组织或者成像区域包含大量散射粒子,其结构小于或等于超声波长。
目前存在许多对斑点特征进行描述与应用的方法,主要有基于统计[4-6]、基于模型[7-11]、信号处理[12-13]和几何方法[14-17]。其中,基于统计的方法因其简单有效性逐渐引起人们重视,并得到了广泛的发展。人们已从射频信号(RF)和包络信号(超声图像)两个方面研究斑点统计分布模型,通过统计模型的参数估计,包括最大似然估计、最大后验估计(MAP)和EM算法[18],获取各器官组织特征。斑点服从一定概率分布,IVUS斑块所产生的斑点属于完全成熟型斑点,基于完全成熟型斑点,学者们提出了3种模型:瑞利混合分布模型(RMM)、Nakagami混合分布模型(NMM)和伽马混合分布模型(GMM)。其中文献[19]用RMM模型描述斑点并对油脂斑块、纤维斑块和钙化斑块进行分类,首先,用EM算法估计斑点的概率模型参数,得到概率混合模型,然后再结合斑块组织的纹理特征对斑块分类。文献[20]提出Nakagami混合分布模型,该模型是瑞利混合模型的推广:瑞利分布仅有一个自由参数,而Nakagami分布有2个自由参数。这两个模型根据超声射频信号形成的物理过程推导得出,应用到临床B型超声图像分析,其效果并不如另一种模型,这就是文献[2]中提到的伽马混合模型,该文中分别用伽马混合模型、瑞利混合模型和Nakagami混合模型来估计IVUS图像中组织的概率分布,采用KL和KS检验评价实验结果,发现伽马混合模型优于Nakagami混合模型,Nakagami混合模型优于瑞利混合模型。
上述研究认为斑点服从单一类型分布,并且指出用伽马混合模型描述斑点概率分布最好,本文在其研究基础上,采用高斯混合模型和伽马混合模型这2种分布类型,分别对IVUS图像中斑块与正常血管组织进行模型估计,在不同概率成分个数取值情况下,分别用2种概率混合模型对斑块和正常血管图像进行概率拟合;然后,用KS、KL检验和相关系数等三种指标评价实验结果,发现:钙化斑块和正常血管区域的斑点概率分布符合高斯混合模型,而软斑块更接近伽马混合模型。说明针对不同组织,可分别选择高斯混合模型和伽马混合模型对其进行描述。本文利用所研究的概率模型,构建高斯伽马混合模型,并提出一种结合邻域信息的概率混合模型,采用最大后验概率准则,实现IVUS图像中各组织图像分割,并与文献[21-23]中混合模型用于图像分割的方法比较,证明本文方法的优越性。
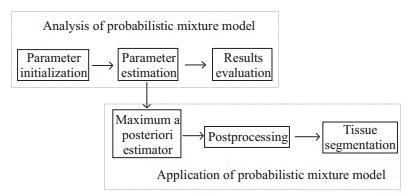
1 方法与流程实验方法包含3个部分:首先简要描述本文所采用的概率混合模型;然后介绍对混合模型效果进行评价的3种指标;最后说明结合邻域信息的混合模型用于图像分割的具体方法。实验流程如图 1所示。
|
图 1 实验流程图 Figure 1 Experimental flow chart. |
混合模型是指随机变量x的概率密度表示为:
| $p\left( {x|\Theta } \right) = \sum\limits_{k = 1}^M {{{\rm{ \mathit{ π} }}_k}{p_k}\left( {x|{\theta _k}} \right)} $ | (1) |
其中
| $p\left( {x|\Theta } \right) = \sum\limits_{k = 1}^M {{{\rm{ \mathit{ π} }}_k}\frac{1}{{\sqrt {2{\rm{ \mathit{ π} }}\sigma _k^2} }}} \exp \left( { - \frac{{{{\left( {x - {\mu _k}} \right)}^2}}}{{2\sigma _k^2}}} \right)$ | (2) |
参数集Θ =(π1, …, πM, θ1, …, θM),θM =(μM, σM)。
若每一个分量都满足伽马分布,则称其为伽马混合模型,表达式为:
| $\begin{array}{l} {p_x}\left( {x|\Theta } \right) = \sum\limits_{k = 1}^M {{{\rm{ \mathit{ π} }}_k}\frac{{{x^{{\alpha _k}}}}}{{\beta _k^{{\alpha _k}}\Gamma \left( {{\alpha _k}} \right)}}\exp \left( { - x/{\beta _k}} \right)} ,\\ x \ge 0,\alpha ,\beta > 0 \end{array}$ | (3) |
其中Γ(x)为欧拉伽马函数,定义:
Θ= (π1, …, πM, θ1, …, Mθ),θM =(αM, βM)。
在这里,已知样本数据和概率密度表达形式,利用EM算法可以估计出未知参数Θ的值,从而得到感兴趣样本的混合分布模型。
1.2 实验效果评价指标本文采用3种指标对概率模型估计的效果进行评估,分别是:KS检验、KL散度值和相关系数值[2]。
KS检验体现累积概率密度间的差异,表达式为:
| ${D_{KS}}\left( {{F_n},{F_X}} \right) = {\rm{sup}}\left| {\widehat {{F_n}}\left( {{x_i}} \right) - \widehat {{F_X}}\left( {{x_i}} \right)} \right|$ | (4) |
其中,
KL散度体现实际概率密度值与模型估计概率密度值之间的差异,表达式为:
| ${D_{KL}}\left( {{p_n},{f_X}} \right) = \sum\limits_{i = 1}^N {{p_n}\left( {{x_i}} \right)\log \frac{{{p_n}\left( {{x_i}} \right)}}{{{f_X}\left( {{x_i}} \right)}}} $ | (5) |
其中pn表示实际概率密度值,fX表示模型估计概率密度值。DKL表示的是概率密度间的差异,因此,DKL越小,概率模型估计效果越好。
相关系数体现实际概率密度值与模型估计概率密度值间相关性的大小,在以上KS、KL检验的基础上,相关系数值越大,概率模型估计效果越好。表达式为:
| ${D_{cc}} = \frac{{\sum\limits_{i = 1}^N {\left( {{p_n}\left( {{x_i}} \right) - \overline {{p_n}} } \right)\left( {{f_X}\left( {{x_i}} \right) - \overline {{f_X}} } \right)} }}{{\sqrt {\sum\limits_{i = 1}^N {{{\left( {{p_n}\left( {{x_i}} \right) - \overline {{p_n}} } \right)}^2}} } \sqrt {\sum\limits_{i = 1}^N {{{\left( {{f_X}\left( {{x_i}} \right) - \overline {{f_X}} } \right)}^2}} } }}$ | (6) |
实验数据的实际概率密度由高斯核平滑概率密度估计函数[24]求得,它是直方图概率密度估计的拓展,已被广泛应用于数据概率密度估计,在matlab中可以直接调用依据该原理所编写的ksdensity函数对数据进行概率密度估计。
本文通过以上3种指标对概率混合模型估计的结果进行评判,当某一种概率模型估计结果的3种指标中2个或以上都是相应指标中最优值时,说明这种模型的估计效果更好。
1.3 图像分割模型传统混合模型由单一的分布类型混合得到,本文借鉴文献[25]中混合模型的创建方法,用高斯和伽马2种分布类型构建高斯伽马混合模型,模型表示如下:
| ${f_X}\left( {{x_i}|{\Theta _k}} \right) = \left\{ \begin{array}{l} {{\rm{ \mathsf{ π} }}_k}{f_1}\left( {{x_i}|{\Theta _k}} \right),1 \le k \le m\\ {{\rm{ \mathsf{ π} }}_k}{f_2}\left( {{x_i}|{\Theta _k}} \right),m \le k \le M \end{array} \right.$ | (7) |
其中,f1(x)表示x服从高斯分布,f2(x)表示x服从伽马分布。
因传统概率混合模型的图像分割方法没有考虑像素间的空间关系,所以可能出现以下情况(图 2)。

|
图 2 噪声图 Figure 2 Noisy image. |
如图 2所示,A、B图的中心点均为噪声点,用传统的概率混合模型会将其与周围像素分为不同的类,为消除噪声点对图像分割结果的影响,文献[22]中提到对像素点后验概率添加邻域信息,但改善效果不大;文献[23]中提出噪声平滑因子的思想,但会出现平滑过渡,细节丢失等问题。考虑到后验概率与像素先验概率πk和条件概率p(xi|Θk)直接相关,本文结合像素间空间关系对混合模型作以下改进:
(1)对像素先验概率πk添加空间信息。例如,在图 2中,A图里所有像素本应属于同一类,但因噪声点x(2, 2)的影响,可能将其与周围像素分为2类。加入空间信息后,所有像素点都受周围像素影响,消除噪声点干扰,所有像素分为同一类。
(2)对条件概率 p(xi|Θk)添加空间信息。依据传统概率混合模型,相同灰度值的像素具有相同的条件概率。在图 2中,图A中心像素与图B周围像素灰度值相同,但它们不属于同一类,传统混合模型不能正确区分两者。加入空间信息后,除灰度值外,所有像素还受周围像素约束,从而能更好地对像素进行划分。具体实现方法如下:
| $p\left( {{x_i}|{\Theta _k}} \right) = \sum\limits_{m \in {N_i}} {\frac{{{\omega _m}}}{{{R_i}}}p\left( {{x_m}|{\Theta _k}} \right)} $ | (8) |
| ${{\rm{ \mathit{ π} }}_{i,j}} = \frac{{\sum\limits_{m \in {\partial _i}} {{\omega _m}{z_{m,j}}} }}{{\sum\limits_{k = 1}^M {\sum\limits_{m \in {\partial _i}} {{\omega _m}{z_{m,k}}} } }}$ | (9) |
其中zi, j是EM算法中的中间变量,此处zi, j计算如下:
| $z_{i,j}^{\left( {k + 1} \right)} = \frac{{{\rm{ \mathit{ π} }}_{i,j}^{\left( k \right)}\sum\limits_{m \in {N_i}} {\frac{{{\omega _m}}}{{{R_i}}}p\left( {{x_m}|\Theta _j^{\left( k \right)}} \right)} }}{{\sum\limits_{h = 1}^M {{\rm{ \mathit{ π} }}_{i,h}^{\left( k \right)}} \sum\limits_{m \in {N_i}} {\frac{{{\omega _m}}}{{{R_i}}}p\left( {{x_m}|\Theta _h^{\left( k \right)}} \right)} }}$ | (10) |
Ni表示第i个像素的邻域,∂i = Ni -{i},表示第i个像素的邻域但不包含第i个像素。ωm是邻域像素的权重,Ri是权重的归一化系数:
| ${R_i} = \sum\limits_{m \in {N_i}} {{\omega _m}} $ | (11) |
本文采用3 × 3的均值模板对像素添加空间信息约束,ωm计算如下:
| ${\omega _m} = \frac{1}{{{{\left( {2{\rm{ \mathit{ π} }}{\delta ^2}} \right)}^{1/2}}}}\exp \left( { - \frac{{d_{m,i}^2}}{{2{\delta ^2}}}} \right)$ | (12) |
| $\delta = \frac{{M \times N - 1}}{4}$ | (13) |
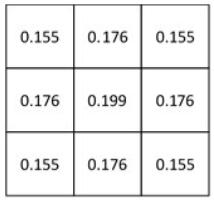
dm, i表示邻域像素m与中心像素i之间的距离,由公式(12)可以看出,邻域像素距中心像素越远,其权重越小,越近则权重越大。M、N分别表示模板窗口的长和宽,本文窗口大小为3 × 3,即M × N = 9,故δ = 2。可计算出均值模板(图 3)。
|
图 3 均值模板 Figure 3 Mean template. |
为避免无噪声图像应用均值滤波时造成图像部分细节丢失问题,在本文中,运用均值滤波时,增加噪声判断。当中心像素灰度值是邻域像素中最大或最小值时,认定它是噪声点,使用均值滤波;否则,不对中心像素点作任何改变。这样既能很好地结合像素点空间关系,有效抑制噪声干扰,又能保持图像细节,从而提高图像分割精度。
图像的分割标准是最大后验准则。首先,用高斯伽马混合模型对IVUS图像进行估计,获得每一个像素点的后验概率,然后根据最小错误率贝叶斯决策完成每个像素的分类,从而完成图像的初步分割。因初步分割图像中仍然会存在一些未被正确分割的孤立点,在此基础上,采用K近邻法对分割图像作后处理,经过后处理,图像分割结果会有较大改善。
2 结果本文分别用高斯混合模型、伽马混合模型对IVUS图像中的组织进行概率模型估计。实验数据取自临床数据库,在临床医生指导下,从实验图像中选取感兴趣区域,感兴趣区域包括钙化斑块、软斑块和正常血管,其中钙化斑块选自12幅IVUS图像,软斑块选自10幅IVUS图像,正常血管选自8幅IVUS图像。为了分析不同混合模型和概率成分个数对实验结果的影响,采用KL、KS检验和相关系数评价模型效果,即对各类组织感兴趣区域构建混合概率模型,计算3种指标值,再分别取平均值。比如:从12幅IVUS图像中,选取钙化斑块区域,分别计算出两种混合模型的3种指标值,最终对12幅图像实验结果取平均值。比较两种概率模型的实验结果,选择高斯伽马混合模型,采用结合邻域信息的混合模型的方法,利用最大后验概率估计准则完成IVUS组织分割。
2.1 IVUS各组织概率混合模型分析在本节实验过程中,首先,选择IVUS图像感兴趣区域,包括钙化斑块、软斑块和正常血管。根据斑块回声的强弱,以血管壁外膜回声为标准,斑块定义如下[26]:
(1)软斑块:软斑块的回声弱于血管壁外膜的回声。包括脂质、疏松和细胞性纤维组织。其中脂质常常表现为周围有高回声区或者纤维帽覆盖的低回声或者无回声区,而疏松和细胞性纤维组织则表现为低回声区。
(2)钙化斑块:钙化斑块的回声强于血管壁外膜回声,而且后方有清楚的声影,钙化组织占管腔周径大于90°。
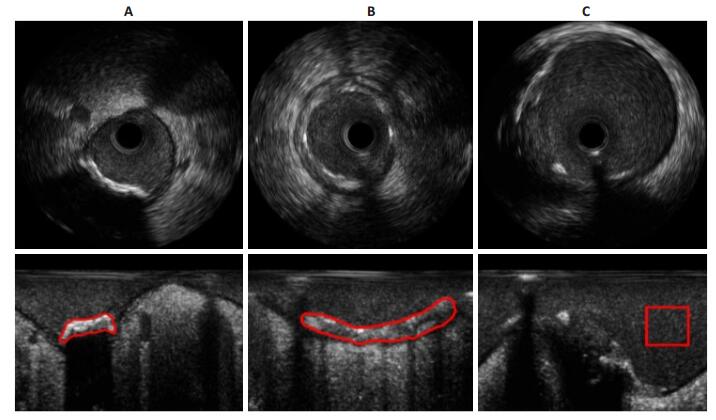
图 4为IVUS实验图像。通过EM算法,分别用两种混合模型对IVUS各组织估计公式(2)、(3)中未知参数,获得模型估计概率估计密度值fX。在这里,由2.2中所介绍的ksdensity函数求出各组织实际概率密度值pn,结合公式(4)、(5)、(6),计算KS、KL和相关系数值,得到两种概率模型在各组织概率估计的定量分析结果(图 5)。
|
图 4 实验原图(红色区域为实验感兴趣区域) Figure 4 The original image showing the area of interest (encircled in red). A-C: IVUS of calcified plaques, soft plaques and normal vascular in Cartesian coordinates and polar coordinates, respectively. |
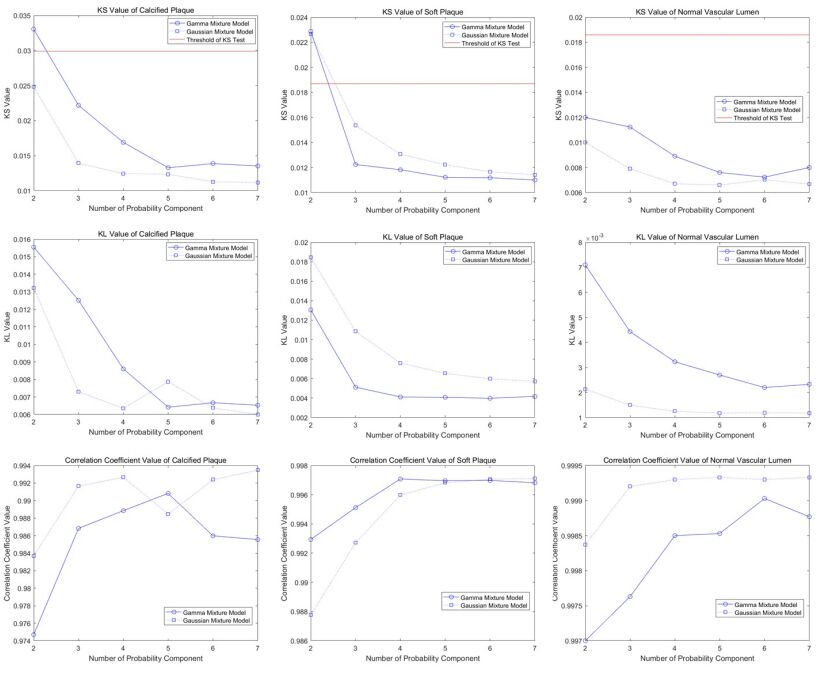
|
图 5 各评判指标对比图(每一列由上到下分别对应各组织相应指标图) Figure 5 Line chart for comparing each evaluation index of different tissues. |
在图 5中,每一行表示不同组织两种概率混合模型的同一评价指标值,在第一行KS值中,可以看到:当M>2时,各组织成分的KS值均小于相应阈值,符合概率模型假设;在M=2时,钙化斑块和软斑块混合模型KS值比阈值大,因IVUS图像中斑块区域面积较小,即试验中样本数较少,故概率拟合精度不够。
在图 5中,每一列表示同一组织两种概率混合模型的不同评价指标值,在A列所对应钙化斑块各指标值中,比较高斯混合模型和伽马混合模型三种指标值,可以看到,高斯混合模型KS、KL值都比伽马混合模型小,同时相关系数值都比伽马混合模型大,这表明在IVUS钙化斑块组织中,高斯混合模型优于伽马混合模型,即高斯混合模型更符合钙化斑块。以此类推,从B、C列图可得出相应结论:伽马混合模型更符合软斑块,高斯混合模型更符合正常血管。
在上述对概率混合模型选择分析基础上,进一步说明概率成分个数M值对概率估计的影响。考察图 5中每一幅折线图,可知:随着M值增大,KS值和KL值呈下降趋势,而相关系数值也呈上升趋势。这表明:概率成分个数M值越大,概率拟合的效果越好;但当M取值在5附近时,曲线变化趋于平缓,这说明M取值为5时混合模型的估计效果接近理想。因此实际应用中为了减小算法的运算时间,模型个数可以在5附近进行选取。
2.2 结合邻域信息的概率混合模型用于图像分割在这里,本文提出结合邻域信息的混合模型用于图像分割,以仿真图、自然图像和IVUS图像为实验对象。对于仿真图和自然图像,本文用结合邻域信息的高斯混合模型完成图像分割,并与现有混合模型方法[21-23]比较,证明了本文方法有效性(图 6、7)。对于IVUS图像,分别用现有混合模型[21-23]、结合邻域信息的高斯混合模型和高斯伽马混合模型完成图像分割,并给出不同组织成分的概率映射图,概率映射图反映了分割图像区域属于某一种组织的概率,能帮助医师更直观地看出图像分割的各组织结构(图 8、9)。

|
图 6 仿真图分割结果 Figure 6 Segmentation results of a simulated image. A-B:Simulation image and the experimental image with speckle noise; C-F: Segmentation results with Gaussian mixture model in 3 previous studies [21-23] and in this study, respectively. |

|
图 7 自然图像分割结果 Figure 7 Segmentation results of natural image. A: Original image; B-E: Segmentation results with Gaussian mixture model in 3previous studies [21-23] and in this study, respectively. |

|
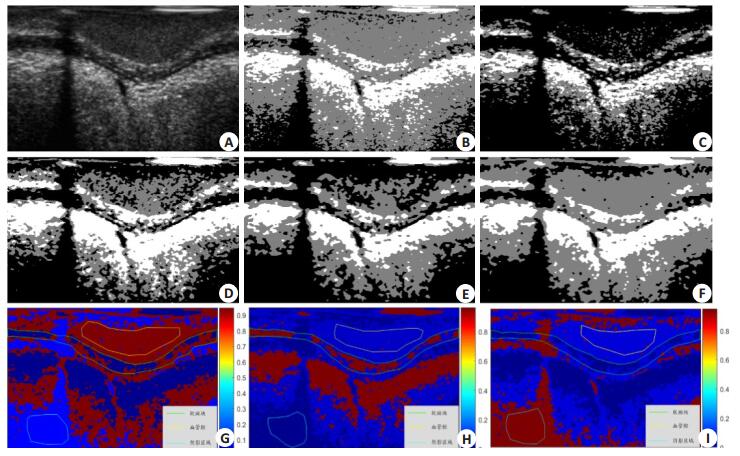
图 8 钙化斑块IVUS分割结果 Figure 8 Segmentation results of an IVUS image with calcified plaques. A: Original image; B-F: Segmentation results with Gaussian mixture model in previous studies[21-23] and with Gaussian mixture model and Gaussian-Gamma mixture model in this study; G-I: Probabilistic mapping of the vascular lumen, calcified plaques and shadow region. |
|
图 9 软斑块IVUS分割结果 Figure 9 Segmentation results of another IVUS image with soft plaques. A: Original image; B-F: Segmentation results with Gaussian mixture model in previous studies[21-23] and with Gaussian mixture model and Gaussian-Gamma mixture model in this study; G-I: Probabilistic mapping of the vascular lumen, soft plaques and shadow region. |
针对以上图像分割的结果,通过定性、定量分析,比较本文分割方法与现有分割方法[21-23]的优劣性。其中,定量分析中利用到结构相似性、误分率和峰值信噪比这3种指标。
在图 6中,图C和图D抗噪性较差,图像轮廓受噪声腐蚀严重。图E和图F保持了图像轮廓,但图E中仍残留较多噪声,而图F则有效地抑制了噪声干扰。计算现有方法和本文方法实验结果的结构相似性、误分率和峰值信噪比(表 1)。
| 表 1 各方法定量评估 Table 1 Quantitative evaluation of each method |
可知,文献[23]中方法和本文方法结果远好于前两种方法,对比文献[23]和本文方法,本文方法在结构相似性和峰值信噪比上比文献[23]中方法提高了分别为2.2%和29.4%,此外,误分率比该方法降低了68.0%,可见本文方法比现有方法有更大优势。
在图 7中,图B和图C受背景中噪点影响较大,B图中相机细节丢失,人物轮廓含较多噪点。C图中人物和相机细节分割效果比B好,但后方建筑物没有与周围背景区分开。D图整体受周围噪声影响较小,但细节丢失较多,比如人物轮廓有毛刺,照相机细节模糊,相机支架与背景融合,而E图则弥补了D图的缺陷。计算现有方法和本文方法实验结果的结构相似性如下表 2。
| 表 2 各方法定量评估 Table 2 Quantitative evaluation of each method |
比较表中各方法分割结果的结构相似性,本文方法比文献[21]中方法提升了3.8%,比文献[23]中方法提升了4.1%。无论视觉效果还是理论数据分析,本文方法均优于现有方法。
在图 8中,实验原图中有3类成分:血管腔、钙化斑块和阴影区域。观察到,D、E、F图分割结果明显优于B、C图,其中,D图中血管腔区域噪声点较多,而E、F图则干净很多,说明本文结合邻域信息的混合模型法的分割结果明显优于现有混合模型法;E图和F图都能将钙化斑块很好地分割出来,但F图中噪声点比E图少很多,区域分割更完整,说明高斯伽马混合模型优于高斯混合模型。G、H、I图分别为血管腔、钙化斑块和阴影区域所对应的概率映射图。以图G举例说明,图中,红色区域表示血管腔,其概率值最大,蓝色部分为背景区域,概率值较小。
在图 9中,实验原图中有3类成分:血管腔、软斑块和阴影区域。可以看到,B图没有将阴影区域从血管腔区域分离干净,且噪点较多,C图误将血管内腔区域划分为阴影区域,D、E图较好地分割开各区域,但两图中血管内腔区域噪声点较多,区域分割不完整;而F图则很好地弥补了这些不足,分割区域连贯且干净,进一步说明本文高斯伽马混合模型法优于现有混合模型法。G、H、I图分别为血管腔、软斑块和阴影区域所对应的概率映射图。以图H举例说明,图中,绿色线所标记的红色区域为软斑块,其概率值最大,浅蓝色区域为血管腔,深蓝色区域为阴影区域,两者概率值都较小。
血管内超声斑点的像素强度符合一定的概率分布,本文用伽马混合模型和高斯混合模型来估计钙化斑块和软斑块所产生斑点和正常血管腔的概率分布,KS检验结果表明这两种分布能很好地描述斑点和正常血管腔的统计特性。此外,用KS、KL和相关系数这3种指标评价两种概率模型估计结果,得出结论:钙化斑块和正常血管腔用高斯混合模型拟合其分布效果更好;而软斑块则用伽马混合模型拟合其分布效果更好。基于这个结论,在具体IVUS图像分割中,依据图像中各组织分布情况,确定用哪一种概率混合模型进行图像分割。在IVUS图像分割中,本文用上述两种模型构建高斯伽马混合模型,并结合像素空间关系,以最大后验概率准则对图像进行分割。经试验结果验证,本文所提出的结合邻域信息的混合模型优于现有混合模型,不仅提高了分割精度,而且有效地抑制了噪声干扰。但因为基于概率混合模型的分割方法主要依据的是图像的灰度信息,所以易将IVUS图像中纹理特征区别较小,灰度值接近的区域划分为同一类。考虑到灰度值接近但属于不同组织的区域间有分界区域,故解决方法有:(1)、临床医生可对比原图和分割图像确定灰度值相近区域边界,从而将两区域区分开;(2)、将本文方法与其它基于图像轮廓的分割方法结合,减小对灰度值的依赖,提高图像分割质量。
| [1] | 王哓婧. 散斑跟踪技术在超声心动图图像分析处理中的应用研究[D]. 山东大学, 2006. |
| [2] | Vegas-Sánchez-Ferrero G, Martin-Fernández M, Sanches JM. A gamma mixture model for IVUS imaging[M]. Springer New York, 2014: 155-71. |
| [3] | Cristea A. Ultrasound tissue characterization using speckle statistics [D]. France: Universite Claude Bernard Lyon 1, 2015. |
| [4] | Prager RW, Gee AH, Treece GM, et al. Analysis of speckle in ultrasound images using fractional order statistics and the homodyned k-distribution[J]. Ultrasonics, 2002, 40(1/8): 133-7. |
| [5] | Martí R, Martí J, Freixenet J, et al. Robust speckle detection in ultrasound images: evaluation aspects[C]. Eigth International Conference on Quality Control by Artificial Vision. International Society for Optics and Photonics, 2007: 63560P-10. |
| [6] | Azar AA, Rivaz H, Boctor E. Speckle detection in ultrasonic images using unsupervised clustering techniques [C]. 2011 Annual International Conference of the IEEE Engineering in Medicine and Biology Society(EMBC), 2011: 8098-101. |
| [7] | Cohen FS, Cooper DB. Simple parallel hierarchical and relaxation algorithms for segmenting noncausal markovian random fields[J]. IEEE Trans Pattern Anal Mach Intell, 1987, 9(2): 195-219. |
| [8] | Therrien CW. An estimation-theoretic approach to terrain image segmentation[J]. Comp Vis Graph Image Proc, 1983, 22(3): 313-26. DOI: 10.1016/0734-189X(83)90079-8. |
| [9] | Mandelbrot BB. The fractal geometry of nature[M]. London: Macmillan, 1983. |
| [10] | Garra BS, Krasner BH, Horii SC, et al. Improving the distinction between benign and malignant breast lesions: the value of sonographic texture analysis[J]. Ultrasonic Imaging, 1993, 15(4): 267-85. DOI: 10.1177/016173469301500401. |
| [11] | Asvestas P, Golemati S, Matsopoulos GK, et al. Fractal dimension estimation of carotid atherosclerotic plaques from B-mode ultrasound: a pilot study[J]. Ultrasound Med Biol, 2002, 28(9): 1129-36. DOI: 10.1016/S0301-5629(02)00550-1. |
| [12] | Mulet-Parada M, Noble JA. 2D+T acoustic boundary detection in echocardiography[J]. Med Image Anal, 2000, 4(1): 21-30. DOI: 10.1016/S1361-8415(00)00006-2. |
| [13] | Yoshida H, Casalino DD, Keserci B, et al. Wavelet-packet-based texture analysis for differentiation between benign and malignant liver tumours in ultrasound images[J]. Phys Med Biol, 2003, 48(22): 3735-53. DOI: 10.1088/0031-9155/48/22/008. |
| [14] | Ojala T, Pietikainen M, Harwood D. A comparative study of texture measures with classification based on feature distributions[J]. Pattern Recognit, 1996, 29(1): 51-9. DOI: 10.1016/0031-3203(95)00067-4. |
| [15] | Petrou M, Sevilla PG. Image Processing: Dealing with Texture [M]. DBLP, 2006. |
| [16] | Caballero KL, Barajas J, Pujol O, et al. In-vivo ivus tissue classification: a comparison between rf signal analysis and reconstructed images[C]. Springer Berlin Heidelberg, 2006: 137-146. |
| [17] | Roundhill DN. Ultrasound time domain velocity measurement[D]. Duke University, 1991. |
| [18] | Qin Y, Priebe CE. Maximum L q-Likelihood estimation via the Expectation-Maximization algorithm: a robust estimation of mixture models[J]. J Am Stat Assoc, 2013, 108(503): 914-28. DOI: 10.1080/01621459.2013.787933. |
| [19] | Seabra JC, Ciompi F, Pujol O, et al. Rayleigh mixture model for plaque characterization in intravascular ultrasound[J]. IEEE Trans Biomed Eng, 2011, 58(5): 1314-24. DOI: 10.1109/TBME.2011.2106498. |
| [20] | Mohana Shankar P. A general statistical model for ultrasonic backscattering from tissues[J]. IEEE Trans Ultrason Ferroelectr Freq Control, 2000, 47(3): 727-36. DOI: 10.1109/58.842062. |
| [21] | Jain AK, Duin RPW, Mao J. Statistical pattern recognition: A review[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2000, 22(1): 4-37. DOI: 10.1109/34.824819. |
| [22] | Prakash RM, Kumari R. Gaussian mixture model with the inclusion of spatial factor and pixel re-labelling: application to Mr brain image segmentation[J]. Arabian J Sci Engin, 2017, 42(2): 595-605. DOI: 10.1007/s13369-016-2278-0. |
| [23] | 赵泉华, 石雪, 王玉, 等. 可变类空间约束高斯混合模型遥感图像分割[J]. 通信学报, 2017, 38(2): 34-43. DOI: 10.11959/j.issn.1000-436x.2017026. |
| [24] | Bowman AW, Azzalini A. Applied smoothing techniques for data analysis: the kernel approach with S-Plus illustrations[J]. J Am Stat Assoc, 1997, 94(447): 982-3. |
| [25] | 侯一民, 唐玥, 孙晓雪, 等. 高斯-瑞利混合模型在遥感图像分割中的应用[J]. 光学学报, 2015, 35(A01): 124-31. |
| [26] | 李虹. 血管内超声图像处理与分析若干技术研究[D]. 南京航空航天大学, 2009. http://d.wanfangdata.com.cn/Thesis/Y1854990 |
 2017, Vol. 37
2017, Vol. 37

