动态脑灌注CT成像技术近年来已经广泛用于急性中风和慢性脑血管性疾病的诊断中，尤其在脑血流动力学参数的定量和定性评估方面具有重要的诊断作用^[1-2]。脑血流动力学参数通常是根据扫描得到的脑灌注CT序列图像，基于体素点或者感兴趣组织区域提取对应的时间密度曲线 (TDC) 和动脉输入函数 (AIF)，利用奇异值分解 (SVD) 或者其改进方法进行计算得到^[3]。而在临床应用中，为了得到准确的血流动力学参数需要对患者病灶区域进行重复的动态扫描，从而大大增加了病人所受的辐射剂量。而研究报告表明，过高的X射线辐射将会诱发癌症、白血病或者其他遗传性疾病^[4-5]。为了减少脑灌注CT的辐射剂量，一种最简单易行的方式是降低脑灌注CT扫描时的毫安秒 (mAs)。然而低mAs条件下所采集得到的投影数据常常受到量子噪声的干扰，使得重建图像含有严重的噪声和伪影，图像质量出现严重退化，进而影响灌注参数的评估与诊断。因此，如何在降低辐射剂量的条件下得到满足临床诊断需求的脑灌注CT图像，已成为CT成像领域内重要的研究课题之一。

为了解决脑灌注CT成像中的上述问题，已有文献[6-17]提出各类方法用于低剂量脑灌注CT图像的恢复，这些方法大多以脑灌注CT序列图像为着力点，通过对序列图像的噪声特性进行建模，一是构建图像滤波器或者图像恢复模型进行图像降噪^[7-12]，二是引入相应的正则化约束到去卷积模型直接计算脑灌注参数^[14-17]。然而，低剂量脑灌注CT图像的噪声统计特性极为复杂，仍未有准确的噪声统计模型，而在投影域，针对低剂量CT投影数据的噪声模型有着广泛深入的研究^[18]。根据投影数据的统计特性，通过构建基于惩罚加权最小二乘 (PWLS) 准则的投影数据恢复模型进行投影数据降噪，可以有效去除CT图像中的噪声和伪影^[19-20]。

基于低剂量脑灌注CT投影数据的统计特性，本文重点研究了投影域降噪方法在低剂量脑灌注CT成像中的应用，并采用文献[20]提出的基于惩罚加权最小二乘的投影数据恢复方法进行了探讨分析。首先采用基于惩罚加权最小二乘的投影数据恢复方法^[20]对低剂量脑灌注CT序列投影数据进行降噪处理，然后重建脑灌注CT序列图像，并进行脑灌注参数成像。实验中我们采用了临床脑灌注数据进行方法验证与评估。

基于我们先前的研究工作^[18]，低剂量CT投影数据（sinogram）近似服从一种独立高斯分布，其均值和方差满足以下关系：

其中，I_i0是X射线入射强度，${\bar p_i}$和σ_i²分别是沿着X射线透射路径i上sinogram数据y_i对应的均值和方差，σ_e²是背景电子噪声方差。在实际计算中，${\bar p_i}$可以通过估计sinogram中y_i周围3×3邻域内的平均值得到，参数Ii0和σ_e²可以通过CT系统常规校准操作测定。

为了提高低剂量CT重建图像中的信噪比，基于统计建模的投影数据恢复方法已用于去除重建图像中的噪声和伪影^[19-20]。本文，为了减少投影数据恢复对重建图像分辨率的影响，我们采用了Gao等^[20]提出的自适应投影数据恢复方法，用于低剂量脑灌注CT成像。自适应投影数据恢复方法主要包括两步：(1) PWLS投影数据恢复，(2) 自适应加权。接下来我们将对这两个步骤逐一阐述。

根据文献[18]中测量的低剂量CT投影数据的统计模型，基于PWLS准则的投影数据恢复的目标函数表示如下：

其中，p为待估计的理想投影数据，Σ表示对角矩阵，其第i个对角元素σ 2表示sinogram数据y 对应的方差。β为一平滑参数，用以调节保真项与惩罚项之间的权衡程度。R (p) 为惩罚项，表示如下：

其中，N_i表示二维sinogram图像网格中以第i个点为中心的四邻域区域，Median(p(N_i)) 表示该邻域内的中值。

针对 (2) 式中的PWLS目标函数最小化问题，本文采用如下所示修正后的高斯-赛德尔 (Gauss-Seidel, GS) 优化方法进行迭代求解：

其中，m是迭代步数。

为了降低基于PWLS准则的投影数据恢复方法可能引起的重建图像分辨率损失这一影响，本文所采用的自适应投影数据恢复方法，根据低剂量脑灌注CT投影数据的噪声方差，在原始投影数据y和PWLS投影数据恢复后的p之间引入了自适应加权处理步，具体表述如下：

其中，${\tilde y}$代表加权后的投影数据，权重w_i根据（1）式中的方差σ_i²决定，计算公式为${w_i} = \left\{ \begin{array}{l} 1, \;\;\;\sigma _i^2 \le \delta \\ 0, \;\;\;\sigma _i^2 > \delta \end{array} \right.$，其中，δ为阈值因子，与投影数据噪声水平相关。在实验中，δ值一般选定为一个小于95%的投影数据方差的常数值。

低剂量脑灌注CT投影数据降噪处理后，将采用标准的FBP方法进行CT图像重建。为了便于表述，本文所采用的处理方法称为“FBP-PWLS”。

为了验证和评估本文所采用的投影数据恢复方法在低剂量脑灌注CT成像中的有效性，我们通过临床脑灌注CT数据实验分别进行了定性分析和定量分析。

实验中所使用的临床脑灌注CT数据采集自日本东芝公司的CT扫描设备。首先，40 mL碘对比剂碘帕醇（Iopamiron 300; Bayer HealthCare, Berlin, Germany）从右肘前静脉以5 mL/s的速率注入，经过5 s延时，开始进行常规剂量增强扫描，扫描协议如下：管电压为80 kVp，管电流为200 mA，层厚为8 mm，机架旋转速度为1 s，时间分辨率为1 s，总扫描时间为40 s。由于同时重复扫描病人2次以获取对应的低剂量脑灌注CT数据，将会大幅增加病人所受的X射线辐射剂量，给病人带来不必要的致癌风险，在本文中，我们参考已有工作提出的低剂量CT数据仿真技术根据标准剂量脑灌注CT投影数据仿真得到对应的低剂量脑灌注CT投影数据^[11-12]。仿真的低剂量脑灌注CT投影数据对应的管电流约为40 mA，相当于标准剂量的五分之一。

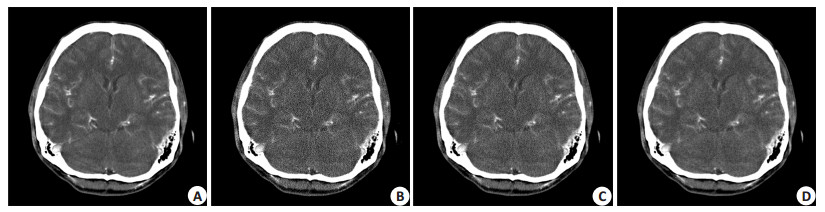
为评估基于PWLS准则的投影数据恢复方法在低剂量脑灌注CT成像中的效果，我们将其与当前临床脑灌注CT设备中广泛应用的常规FBP重建方法 (使用空间不变的低通滤波器) 进行比较。在实验中，空间不变的低通滤波器我们选用Hanning窗，本文所提的FBP-PWLS方法中平滑参数β取值为8×10³。根据脑灌注CT增强图像，我们可以看出，FBP-PWLS方法相较于其他两种方法具有更好的抑制噪声和伪影的能力，所重建的脑灌注CT序列图像与标准剂量的重建结果更为接近 (图 1)。

图 1(Figure 1)

图 1 不同方法重建得到的第15帧脑灌注CT图像 Figure 1 Cerebral perfusion CT images at 15th time-frame reconstructed by different methods. A: Normal-dose (FBP-ramp); B: Low-dose (FBP-ramp); C: Low-dose (FBP-Hann); D: Low-dose (FBP-PWLS).

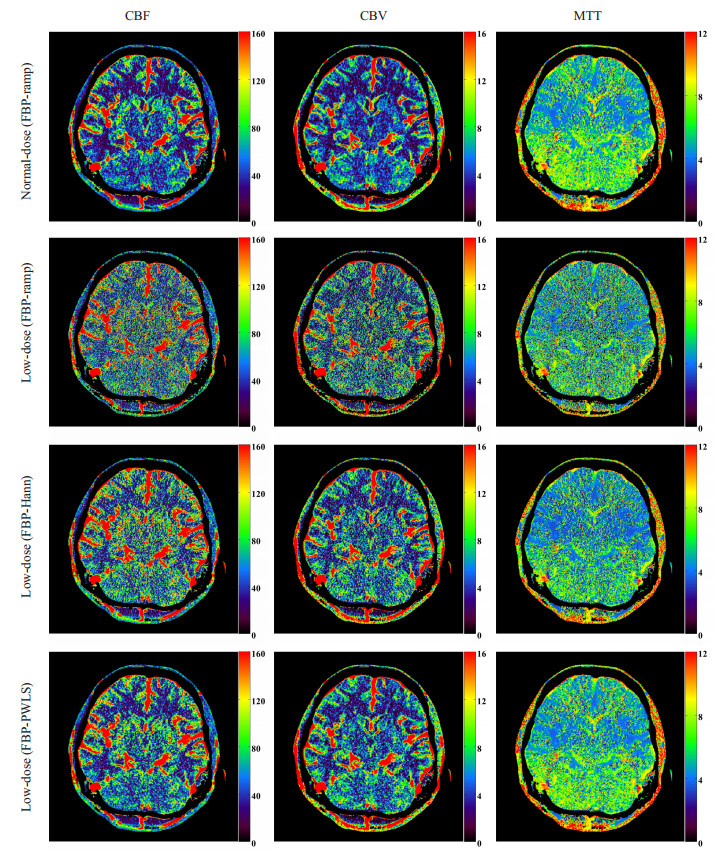
为进一步评估不同方法对脑灌注参数成像的效果，本文根据重建的动态脑灌注CT序列图像采用标准奇异值分解 (sSVD) 方法进行了脑灌注血流动力学参数的计算，分别为脑血流量 (CBF)、脑血容量 (CBV) 和平均通过时间 (MTT)。相较于常规的FBP重建方法，FBP-PWLS方法处理得到的结果，其脑灌注参数图中噪声得到明显抑制，细节和边缘更加清楚，组织与背景更容易区分开，与标准剂量的结果更为接近 (图 2)。

图 2(Figure 2)

图 2 不同处理方法得到的CBF、CBV和MTT脑灌注参数图 Figure 2 CBF, CBV and MTT maps calculated from cerebral perfusion CT images reconstructed by different methods.

通过以上视觉评价，可以看出本文采用的投影数据恢复方法相比常规处理方法对于低剂量脑灌注CT成像有着明显的改善效果，尤其在图像噪声抑制和边缘细节保持方面具有良好的表现。

为了定量比较和分析投影数据恢复方法对低剂量脑灌注CT成像的有效性，本文计算了不同处理方法对应的CBF参数图的峰值信噪比 (PSNR)、均方根误差 (RMSE) 和通用质量指数 (UQI)3个图像质量评价指标值，其计算公式如下：

其中，f 代表低剂量的CBF参数图，f是与之对应的常规剂量CBF参数图，将其作为参考图像。σ是两者的标准差，f_max是参考图像的最大值，n是图像的像素值。σ_f²和σ_f²分别代表指定ROI内的估计参数图和标准参考图的方差，μ_f和μ_f分别为与之对应的均值。

表 1列出了图 2中低剂量脑灌注CBF参数图对应的PSNR、RMSE和UQI 3个图像质量评价指标值。FBP-PWLS方法相比常规的FBP-ramp和FBP-Hann处理方法对应的CBF参数图像具有更高的PSNR值和更低的RMSE值，这表明FBP-PWLS方法对于低剂量脑灌注CT成像具有更优的降噪效果。同时比较UQI值，可以看出FBP-PWLS方法对应的UQI更趋近于1，说明FBP-PWLS对应的CBF参数图更接近于标准剂量的CBF参数图 (表 1)。

表 1(Table 1)

表 1 对应图 2中CBF参数图的PSNR、RMSE和UQI Table 1 PSNR, RMSE and UQI measured on the CBF maps in Fig.2 Method FBP-ramp FBP-Hann FBP-PWLS PSNR (dB) 34.40 36.07 38.78 RMSE 31.89 26.32 19.27 UQI 0.709 0.914 0.954

表 1 对应图 2中CBF参数图的PSNR、RMSE和UQI Table 1 PSNR, RMSE and UQI measured on the CBF maps in Fig.2

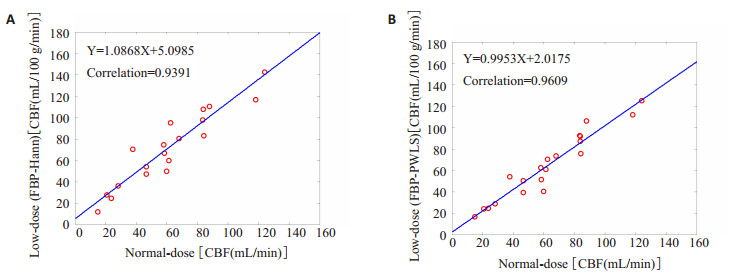
FBP-PWLS方法得到的CBF参数图相比常规FBP-Hann方法的CBF参数图具有更高的相关性系数，这表明在低剂量脑灌注CT成像中，通过采用FBP-PWLS方法可以得到更为接近标准剂量的脑灌注参数图，实现满足临床诊断的需求 (图 3)。

图 3(Figure 3)

图 3 FBP-PWLS和FBP-Hann两种方法对应的CBF参数图的相关性系数 Figure 3 Correlation plots between the CBF values computed from the normal-dose images and the low-dose images reconstructed by FBP-Hann (A) and FBP-PWLS (B) methods.

本文针对低剂量脑灌注CT成像问题，结合CT投影数据的统计特性，探讨了基于惩罚加权最小二乘准则的投影数据恢复方法在低剂量脑灌注CT中的应用。为了评价投影数据恢复方法的有效性，我们采用了临床脑灌注CT数据进行实验。通过与常规处理方法的实验结果比较，本文所采用的投影数据恢复方法能够有效抑制低剂量脑灌注CT图像及其对应的脑灌注参数图中的噪声与伪影。在扫描剂量降低为标准剂量1/5的情况下，投影数据恢复方法处理得到的低剂量脑灌注CT图像及脑灌注参数图更接近于标准剂量参考图像。与其他已有的方法相比，如Niu等^[9]根据脑灌注CT序列图像间的低秩稀疏特性构建的低秩与全变分最小双重约束的图像恢复方法，以及基于正则约束的迭代去卷积方法^[14-17]，本文所提出的方法不仅有效地抑制了噪声和伪影，还跳出了传统方法局限于序列图像本身和直接图像后处理的局限，充分考虑了噪声的统计特性，这对于低剂量脑灌注成像在临床诊断中有着重要的应用意义。接下来，进一步研究和探讨投影域与图像域双重降噪相结合的方法^[21]及其在低剂量脑灌注CT成像中的应用将是下一步开展的工作。