2. 泰安市中心医院彩超室,山东 泰安 271000;
3. 电子科技大学自动化工程学院,四川 成都 611731
2. B-Ultrasound Room, Taian Central Hospital,Tanan 271000, China;
3. School of Electronic Engineering, University of Electronic Science and Technology of China, Chengdu, 611731, China
在磁共振成像(MRI)的临床应用中,强脂肪信号通常会不利于病灶的识别和诊断,其中受影响较大的病症如炎症、水肿、肿瘤等,因此抑制脂肪信号在临床上有着重要意义。当前脂肪抑制技术主要包括频率选择饱和技术[1]、反转恢复技术(STIR)[2]、Dixon技术[3]等。而频率选择饱和技术对主磁场和射频场的均匀性要求较高,STIR技术虽然对主磁场和射频场的依赖性不高,但其图像信噪比较低[4]。与这两种技术相比,Dixon技术对主磁场的不均匀性较不敏感,得到的结果信噪比较高,并能同时得到水图和脂肪图,可为一些临床诊断提供辅助信息[5],如肥胖病人的诊断[6]。
Dixon水脂分离技术发展至今,衍生出了基于单点[7],两点[8-15]和多点的Dixon[16-19]技术,其中两点Dixon技术因其扫描效率较高,且可灵活选择回波时间而有着较高的临床应用需求[4, 10]。在磁共振应用研究中,通常假设主磁场在空间上是缓慢变化的,因此由其变化导致的相位也是空间平滑的[20]。而两点Dixon技术的主要问题就是如何正确的估计出由于场的不均匀性导致的误差相位。假设由主磁场不均匀性导致的误差相位为Φ,可由向量表示为eiΦ[11-14],当Φ是空间平滑时,则向量eiΦ具有空间方向一致性。通常情况下求由主磁场不均匀导致的误差向量eiΦ比直接求误差相位Φ更加简单可行,因为不需要对Φ相位解缠绕,而相位解缠绕算法在某些情况下的可靠性有可能降低,如低信噪比、复杂相位变化等[21-23],并且eiΦ方向具有保持不变的特点。在两点Dixon技术中,每个像素点的误差相位可以求出两个解[9, 11-13],但只有其中一个解是正确的,因此需要找到一个可靠的算法来确定每个像素的正确解。
现有的两点Dixon技术主要分3类,第1类是迭代平滑方法[10, 12],第2类是利用相位平滑假设,求全局最小[11, 14],第3类是利用区域增长算法[13, 15]。在原始的基于区域增长的相位校正算法中,只能利用同反相位的图像得到水和脂肪[8, 15]。随后Ma[13]又提出了基于区域增长的任意回波时间的两点Dixon技术。但是在图像噪声较大、存在伪影和运动等情况下,区域增长算法容易发生误差传播和误差累积[4, 19],从而导致最终结果中发生水脂互换现象,而且运算耗时。针对这个问题,本文提出方法做出了改进,减少了由于误差传播造成的相位误差累积,使结果更加准确和可靠,并降低了运算时间。本文方法主要是把得到的向量图降采样成4幅子图像,然后利用计算机的并行技术同时独立进行基于区域增长的向量校正算法来获得4幅子误差向量图,最后利用平滑约束合并这4 幅子误差向量图得到最终的一幅误差相量图。最后用仿真实验和5组真实数据验证了本文提出的方法。
1 方法 1.1 两点Dixon水脂分离技术原理水和脂肪的氢原子在磁环境下的共振频率有所不同,这个现象也被称为化学位移效应[24]。因此,在磁共振成像当中,可以通过调节回波时间来控制水和脂肪这两个磁化矢量的夹角,然后利用一系列后处理分离出水和脂肪信号。
对于任意回波时间的两点Dixon水脂分离技术,可以构建如下模型:
| $S1=\left( W+{{\delta }_{1}}F{{e}^{i{{\theta }_{1}}}} \right){{P}_{1}}$ | (1) |
| $S2=\left( W+{{\delta }_{2}}F{{e}^{i{{\theta }_{2}}}} \right){{P}_{1}}P$ | (2) |
其中W,F分别代表水和脂肪信号的幅值,TE代表回波时间。S1,S2分别是TE1和TE2时间采集的复数信号,(δ1,δ2)和(θ1,θ2)分别代表在回波时间TE1和TE2下对应的幅度衰减因子和相位夹角[25],已知。P1代表系统的相位误差向量eiΦ0,P代表TE2时间相对TE1累积的额外相位差向量eiΦ。
为了正确求解W和F,需先求出P。假设一个新的变量Q,Q代表水信号占的百分数,表达式如下:
| $Q=\frac{W}{W+F}$ | (3) |
| ${{Q}_{1,2}}=\frac{-{{a}_{2}}\prime \pm \sqrt{{{a}_{2}}{{\prime }^{2}}-4{{a}_{1}}\prime {{a}_{3}}\prime }}{2{{a}_{1}}\prime }$ | (4) |
其中:
| ${{a}_{1}}\prime =\left( 1+{{\delta }_{2}}^{2}2{{\delta }_{2}}\cos {{\theta }_{2}} \right){{M}_{1}}-\left( 1+{{\delta }_{1}}^{2}2{{\delta }_{1}}\cos {{\theta }_{1}} \right){{M}_{2}}$ | (5) |
| ${{a}_{2}}\prime =-2\left[ \left( 1+{{\delta }_{2}}^{2}2{{\delta }_{2}}\cos {{\theta }_{2}} \right){{M}_{1}}-\left( {{\delta }_{1}}^{2}-{{\delta }_{1}}\cos {{\theta }_{1}} \right){{M}_{2}} \right]$ | (6) |
| ${{a}_{3}}\prime =\left( {{M}_{1}}{{\delta }_{2}}^{2}-{{M}_{2}}{{\delta }_{1}}^{2} \right)$ | (7) |
M1和M2分别是信号S1和S2的平方。利用水分数Q和图像中的相位信息来构建如下两个和P同方向的向量:
| $A\prime ={{S}_{1}}^{*}{{S}_{2}}\left[ {{Q}_{1}}+{{\delta }_{1}}\left( 1-{{Q}_{1}} \right){{e}^{i{{\theta }_{1}}}} \right]\left[ {{Q}_{1}}+{{\delta }_{2}}\left( 1-{{Q}_{1}} \right){{e}^{-i{{\theta }_{2}}}} \right]$ | (8) |
| $B\prime ={{S}_{1}}^{*}{{S}_{2}}\left[ {{Q}_{2}}+{{\delta }_{1}}\left( 1-{{Q}_{2}} \right){{e}^{i{{\theta }_{1}}}} \right]\left[ {{Q}_{2}}+{{\delta }_{2}}\left( 1-{{Q}_{2}} \right){{e}^{-i{{\theta }_{2}}}} \right]$ | (9) |
对A'和B'做归一化处理分别得到A和B。
用水分数构成的和P同方向的向量为A或B,而P的正确值只有一个。因此需要利用向量P是空间平滑的假设条件,为每个像素点从(A,B)中选出一个正确的向量,构建正确的向量图P。最后把P代入等式(1)和(2),利用最小二乘方法求解出W和F。
1.2 区域增长算法先定义36个空的像素栈,划分标准为:0°~40°每2°一个栈,共20个;40°~60°每5°一个栈,共4个;60°~180°每10°一个栈,共12个。像素栈的优先级从1到36依次下降,来保证质量较高的像素点优先被处理。像素点进栈标准见等式(10)和(11),出栈规则遵循先进先出原则。进栈标准如下:
| ${{\psi }_{1}}=A*conj\left( {{P}_{s}} \right)$ | (10) |
| ${{\psi }_{2}}=B*conj\left( {{P}_{s}} \right)$ | (11) |
其中Ps表示以当前像素点为中心的矩形块内已确定的像素点的向量和,矩形块的大小为5×5(块的大小由经验值决定)。取ψ 1,ψ 2中较小的一个值作为进栈标准。详细步骤参考文献[13]。
1.3 基于多分辨率图像的两点水脂分离方法提出方法流程图见图 1,详细步骤如下:

|
图 1 算法流程图 Figure 1 Flowchart of the proposed method. |
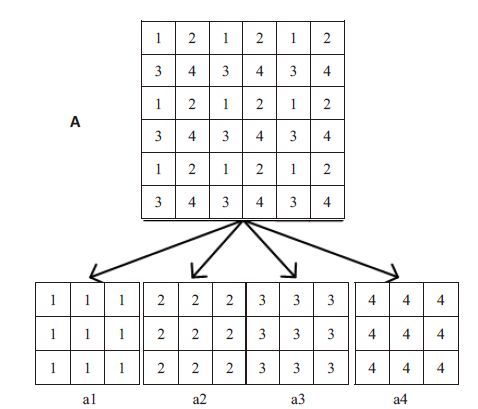
求出场向量图,并对(A,B)进行隔行隔列降采样得到4对子图像(a1,b1)、(a2,b2)、(a3,b3)和(a4,b4)。隔行隔列降采样方式见图 2。
|
图 2 隔行隔列降采样操作 Figure 2 The method of undersample operation. |
对4对子图像分别运用1.2节描述的区域增长算法,得到4幅子场向量图P1、P2、P3和P4。
1.3.3 平滑合并对P1、P2、P3和P4分别做平滑校正和相同空间位置的4个向量之间的平滑校正,然后按像素点原来的位置放回同一场向量图中得到最终的场向量图P,组合过程为步骤1的逆过程。
(a)平滑校正
用均值滤波对场向量图P1进行滤波得到滤波后的场向量图Ps,滤波窗的大小为11×11(窗的大小由经验值确定)。然后用Ps(x,y)分别跟a1(x,y)和b1(x,y)求夹角得到两个夹角值。如果Ps(x,y)和a1(x,y)的夹角值小于Ps(x,y)与b1(x,y)的夹角值,则场向量图P1(x,y)更新为a1(x,y),反之,更新为b1(x,y),其中(x,y)代表像素点的空间坐标。同理,对P2,P3和P4做相同处理。
(b)P1,P2,P3和P4之间的平滑校正
假设最终的场向量图P是空间平滑的,因此相邻的4个点的向量方向也应该是空间平滑的。对场向量图P1,P2,P3和P4在空间(x,y)位置的4个向量分别两两求夹角,如果有某个向量与其它3个向量的夹角中有两个超过30°或有一个超过60°,则认为该场向量图中该点的向量值是错误的,并将其更换为对应的另一个向量。如,P1中位于空间位置(x,y)处的向量为A(x,y),A(x,y)与其它3个子场向量图中对应位置的向量的夹角有一个超过60°,则认为A(x,y)的选取是错误的,应校正为向量B(x,y)。
1.4 平滑校正求解对向量图P平滑校正,得到最终的向量图P。代入等式(1)和(2)中,利用最小二乘方法求解出W和F,得到最终的水脂分离结果。
2 实验 2.1 实验数据实验数据采用ISMRM Challenge 2012 公布的数据[26],该组数据包括两组膝盖数据、两组腹部数据以及一组腿部数据。仿真数据模拟的是具有多个相位突变点的相位数据。
在噪声仿真实验中,原始仿真数据分别加上均值均为零,方差为幅值的1%,5%和10%的随机噪声。
实验平台为HP EliteDesk 800(Intel i7 3.6 GHzRAM: 4 GB),程序采用Matlab2014 实现。
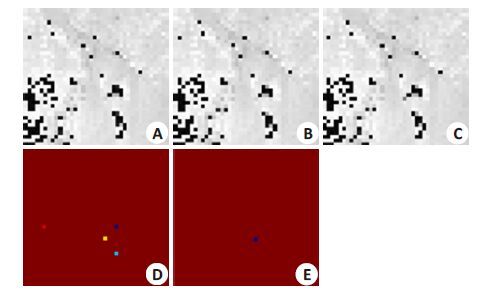
2.2 结果与讨论为了验证在有噪声、伪影等情况下而导致相位发生剧烈变化和突变时提出算法的有效性,图 3给出了仿真实验结果对比,本文选取了一幅大小为41×41,包含多个突变点的相位图作为参考结果,用以模拟发生相位突变的情况,然后分别用全局区域增长[13]算法和本文方法求解。图 3显示了本文方法和全局区域增长算法仿真实验结果对比,图 3A是全局区域增长算法结果,图 3B是本文方法结果,图 3C是参考结果,图 3D是全局区域增长算法和参考结果的对比,图 3E显示的是本文算法和参考结果的对比。
|
图 3 仿真实验结果 Figure 3 Result of simulation test. A: Result of globalregion-growingalgorithm; B: Result of the proposed algorithm; C: Referenceresult; D: Difference in the errors between global region-growingand the reference; E: Difference in errors between the proposedalgorithm and the reference. |
在图 3D中错误的像素点有4个,而提出方法的错误像素点只有一个。该实验结果表明,全局区域增长算法更容易发生误差的累积,而本文提出的方法通过对图像的隔行隔列降采样,使部分子图像跳过一些相位突变点,从而降低对后期相位校正的影响。而且子图像在各自独立的相位校正过程中也能利用全局平滑约束的条件,在一定程度上降低了误差传播和误差的累积,并在最后合并子场向量图时再次利用相位平滑的假设条件,使4幅子场向量图中发生错误的像素点数得到进一步降低。
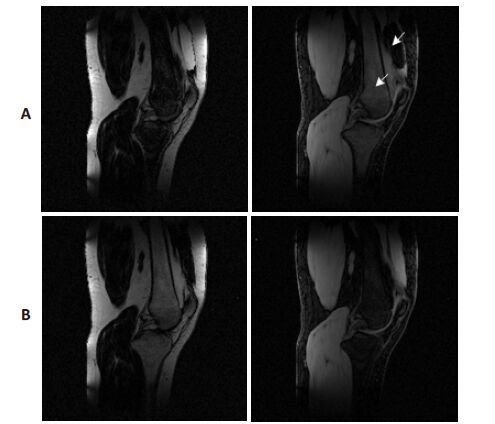
同时为了验证本文方法在真实数据中的有效性,图 4给出的是本文方法和全局区域增长算法[13]膝关节矢状面水脂分离结果。数据采集参数:采集序列是GRE序列,场强1.5 T,TE1=2.4 ms,TE2=5.9 ms,利用多峰值的脂肪模型[17],其中(δ1,δ2)和(θ1,θ2)为(0.87,0.65)和(-189°,64°)。第1列是脂肪图,第2列是水图。第1行是全局区域增长算法的结果,第2行是本文提出方法结果。从图中白色箭头指示处可以看出,全局区域增长算法的结果发生了明显的水脂互换,而本文提出方法实现了水和脂肪的准确分离。全局区域增长算法失败的原因可能是由于在采集的膝盖数据中,受多种组织和空气的影响下,相位发生了急剧的变化,从而导致在误差相位校正的时候发生了错误,使最终的水脂分离结果发生错误。本文提出的方法,通过对图像的隔行隔列降采样,降低突变相位对后期相位校正的影响,从而得到正确的水脂分离结果。
|
图 4 膝关节矢状面水脂分离结果 Figure 4 Water-fat separation result of a sagittal slice of theknee. A: Result of global region-growing method; B: Resultof proposed method. The first column is fat images,and thesecond column is water images. |
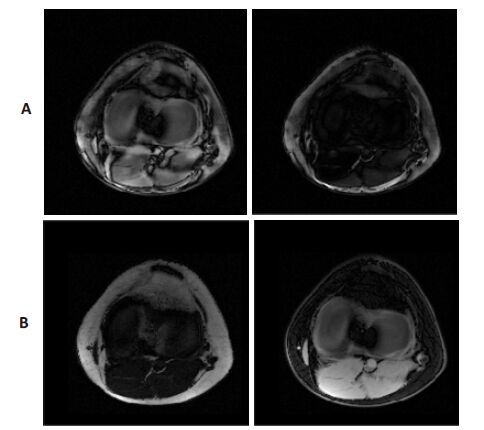
为了验证本文提出的方法更稳定和可靠,图 5给出了本文方法和TRW-S两点Dixon算法[11]膝关节横断面水脂分离结果。TRW-S两点算法是利用相位平滑假设求全局最小的算法。数据采集参数:场强3T,TE1=1.4 ms,TE2=3.1 ms。其中(δ1,δ2)和(θ1,θ2)为(0.86,0.62)和(-158°,74°)。第1行是TRW-S算法结果,第2行是本文方法结果。从图中可以看出TRW-S算法的水脂分离结果很差,而本文方法得到正确水脂分离结果,无明显水脂互换发生。结果表明TRW-S算法在组织结构较复杂部位容易失败。TRW-S算法代码由ISMRM Challenge2012水脂分离工具箱[26]提供。
|
图 5 膝关节横断面水脂分离结果 Figure 5 Water-fat separation result of a cross-sectional sliceof the knee. A: Result of TRW-S method; B: Result of theproposed method. The first column is fat images; thesecond columnis water images. |
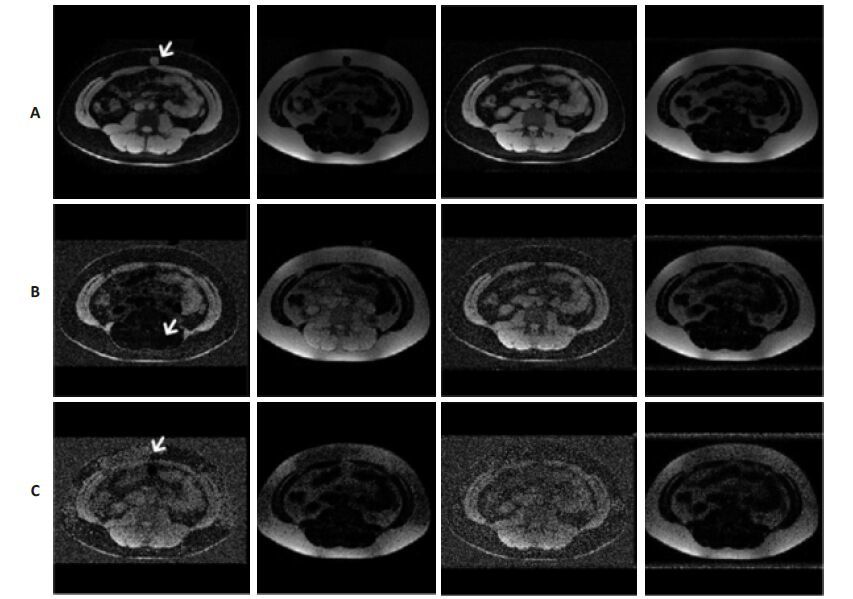
在图 6中本文仿真了噪声对实验结果的影响,第1列是全局区域增长方法结果,第3列是本文方法水脂分离结果。噪声水平A:1%;B:5%;C:10%。从图中可以看出在不同的噪声水平下,本文方法得到的水脂分离结果无错误发生,而全局区域增长算法的结果中则有不同的错误出现(白色箭头所指处)。仿真实验表明,相比于原始的全局区域增长方法,本文方法能够降低噪声对水脂分离结果的影响。
|
图 6 下腹部加入仿真噪声后水脂分离结果 Figure 6 Water-fat separation result of a cross-sectional slice of the abdomen with noise. The left column is globalregion growing method,and the right column is the proposed method. |
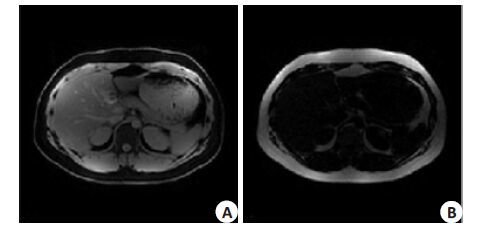
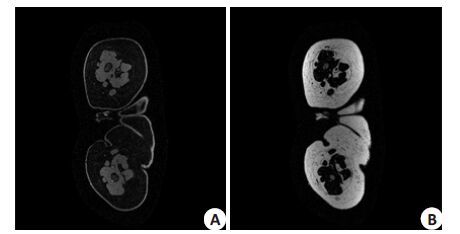
为了验证算法的稳定性,分别做了多组不同部位的真实数据水脂分离实验,图 7是本文方法在上腹部的水脂分离结果。数据采集参数:场强3T,TE1=2.9 ms,TE2=3.6 ms。其中(δ1,δ2)和(θ1,θ2)为(0.70,0.52)和(57°,157°)。A是水图,B是脂肪图。图 8是本文方法在大腿的水脂分离结果。数据采集参数:场强3T,TE1=2.23 ms,TE2=3.34 ms。其中(δ1,δ2)和(θ1,θ2)为(0.79,0.60)和(-39°,120°)。A是水图,B是脂肪图。
|
图 7 上腹部水脂分离结果 Figure 7 Water-fat separation result of a cross-sectional slice of theabdomen. A: Water image; B: Fat image. |
图 7、8的实验中,最终水脂分离结果都没有发生错误。通过上述实验证明,本文提出方法,通过隔行隔列降采得到的低分辨率图像,能有效降低由于区域增长算法导致的误差。表 1是本文方法跟与全局区域增长算法运行时间对比。由于在算法运行方面,本文方法可以利用并行计算技术,整个算法的运行时间要比原始全局区域增长算法快3倍左右,这在图像矩阵较大和三维区域增长的情况下,有明显的时间优势。而且通过多组真实数据的水脂分离实验以及与其它方法的对比,验证了本文提出方法的稳定性和准确性。
|
图 8 大腿水脂分离结果图 Figure 8 Water-fat separation result of a cross-sectional slice ofthe lower limb. A:Water image; B: Fat image. |
| 表 1 算法运行时间对比 Table 1 Calculation time of proposed method and Global RegionGrowing |
针对在噪声、伪影、运动等影响下,区域增长算法容易发生误差传播和误差累积,从而导致水和脂肪分离失败的问题[4, 19],本文将多分辨率和区域增长相结合,提出一种基于多分辨率图像和区域增长的水脂分离方法。与全局区域增长方法相比,能够有效降低误差的累积。与求全局最小的TRW-S方法相比,在解剖结构较复杂的位置,也能准确分离水和脂肪。通过多组真实数据验证,表明本文提出的方法是一种稳定的、可靠的水脂分离方法。
综上所述,本文提出的方法在两点Dixon水脂分离结果中表现的更加鲁棒和可靠,在解剖结构较复杂和存在相位突变的情况下也可以准确的实现水和脂肪的分离。在后续工作中,将把本文方法扩展到三维数据上,并作进一步优化处理。
| [1] | Frahm J, Haase A, H?nicke W, et al. Chemical shift selective MR imaging using a whole-body magnet[J]. Radiology, 1985, 156 (2): 441-4. DOI: 10.1148/radiology.156.2.4011907. |
| [2] | Bydder GM, Young IR. MR imaging: clinical use of the inversion recovery sequence[J]. J Comput Assist Tomogr, 1985, 9 (5): 659-75. |
| [3] | Dixon WT. Simple proton spectroscopic imaging[J]. Radiology, 1984, 153 (8): 189-94. |
| [4] | Eggers H, Boernert P. Chemical shift Encoding-Based Water-Fat separation methods[J]. J Magn Reson Imaging, 2014, 40 (2): 251-68. DOI: 10.1002/jmri.v40.2. |
| [5] | Del Grande F, Santini F, Herzka DA, et al. Fat-Suppression techniques for 3-T MR imaging of the musculoskeletal system[J]. Radiographics, 2014, 34 (1): 217-33. DOI: 10.1148/rg.341135130. |
| [6] | Chebrolu VV, Hines CD, Yu H, et al. Independent estimation of T2*for water and fat for improved accuracy of fat quantification[J]. Magn Reson Med, 2010, 63 (4): 849-57. DOI: 10.1002/mrm.v63:4. |
| [7] | Yu HZ, Reeder SB, Mckenzie CA, et al. Single acquisition water-fat separation: Feasibility study for dynamic imaging[J]. Magn Reson Med, 2006, 55 (2): 413-22. DOI: 10.1002/(ISSN)1522-2594. |
| [8] | Ma JF, Slavens Z, Sun W, et al. Linear Phase-Error correction for improved water and fat separation in Dual-Echo dixon techniques[J]. Magn Reson Med, 2008, 60 (5): 1250-5. DOI: 10.1002/mrm.v60:5. |
| [9] | Rambow O, Hazle J, Clark J, et al. Direct water and fat determination in two-point Dixon imaging with flexible echo times[J]. Med Phys, 2013, 40 (11): 112302. DOI: 10.1118/1.4824692. |
| [10] | Eggers H, Brendel B, Duijndam A, et al. Dual-Echo dixon imaging with flexible choice of echo times[J]. Magn Reson Med, 2011, 65 (1): 96-107. DOI: 10.1002/mrm.v65.1. |
| [11] | Berglund J, Ahlstroem H, Johansson L, et al. Two-point Dixon Method With Flexible Echo Times[J]. Magn Reson Med, 2011, 65 (4): 994-1004. DOI: 10.1002/mrm.22679. |
| [12] | Xiang Q. Two-point water-fat imaging with partially-opposed-phase (POP) acquisition: An asymmetric Dixon method[J]. Magn Reson Med, 2006, 56 (3): 572-84. DOI: 10.1002/(ISSN)1522-2594. |
| [13] | Ma JF, Son JB, Hazle JD. An improved region growing algorithm for phase correction in MRI[J]. Magn Reson Med, 2016, 76 (2): 519-29. DOI: 10.1002/mrm.v76.2. |
| [14] | Zhang T, Chen Y, Bao S, et al. Resolving phase ambiguity in dual-echo dixon imaging using a projected power method[J]. Magn Reson Med, 2016, 25 (5): 28. |
| [15] | Ma J. Breath-hold water and fat imaging using a dual-echo two-point dixon technique with an efficient and robust phasecorrection algorithm[J]. Magn Reson Med, 2004, 52 (2): 415-9. DOI: 10.1002/(ISSN)1522-2594. |
| [16] | Reeder SB, Wen Z, Yu H, et al. Multicoil dixon chemical species separation with an iterative least-squares estimation method[J]. Magn Reson Med, 2004, 51 (1): 35-45. DOI: 10.1002/(ISSN)1522-2594. |
| [17] | Cui C, Wu XD, Newell JD, et al. Fat water decomposition using Globally optimal surface estimation (GOOSE) algorithm[J]. Magn Reson Med, 2015, 73 (3): 1289-99. DOI: 10.1002/mrm.25193. |
| [18] | Wang DH, Zwart NR, Li ZQ, et al. Analytical Three-Point dixon method: with applications for spiral Water-Fat imaging[J]. Magn Reson Med, 2016, 75 (2): 627-38. DOI: 10.1002/mrm.25620. |
| [19] | Cheng C, Zou C, Liang C, et al. Fat-water separation using a region-growing algorithm with self-feeding phasor estimation[J]. Magn Reson Med, 2016, 14 (6): 26. |
| [20] | |
| [21] | Ma J. Dixon techniques for water and fat imaging[J]. J Magn Reson Imaging, 2008, 28 (3): 543-58. DOI: 10.1002/jmri.v28:3. |
| [22] | Maier F, Fuentes D, Weinberg JS, et al. Robust phase unwrapping for Mr temperature imaging using a magnitude-sorted list, multiclustering algorithm[J]. Magn Reson Med, 2015, 73 (4): 1662-8. DOI: 10.1002/mrm.v73.4. |
| [23] | Hong H, Lingda W. PUMA-SPA: a phase unwrapping method based on PUMA and second-order polynomial approximation[J]. IEEE Geoscience Remote Sens Lett, 2014, 11 (11): 1906-10. DOI: 10.1109/LGRS.2014.2313854. |
| [24] | Hood MN, Ho VB, Smirniotopoulos JG, et al. Chemical shift: the artifact and clinical tool revisited[J]. Radiographics, 1999, 19 (2): 357-71. DOI: 10.1148/radiographics.19.2.g99mr07357. |
| [25] | Lim TY , Ma JF. Image-based determination of the fat signal model for Dixon water and fat imaging[C]. In Proceedings of the 20th Annual Meeting of ISMRM, Melbourne, Victoria, Australia, 2012. p 2483. |
| [26] | ISMRM Challenge on water-fat reconstruction[Z]. http://challenge.ismrm.org/node/8. Last accessed June 1, 2016. |
 2017, Vol. 37
2017, Vol. 37

