2. 南方医科大学 广东省医学图像处理重点实验实,广东 广州 510515 ;
3. 天津医科大学总医院放射科,天津 300052
2. Guangdong Provincial Key Laboratory of Medical Image Processing,Southern Medical University,Guangzhou,510515,China ;
3. Department of radiology,General Hospital,Tianjin Medical Universi ty,Tianjin 300052,China
CT心肌灌注成像(CT-MPI)作为一种有效的非侵入功能成像方法,其在冠状动脉疾病(CAD)的诊断和危险分级方面有显著的优势[1]。在CT-MPI的研究中,可以通过心肌灌注数据估计血流动力学参数图,比如心肌血流量(MBF),心肌血容量(MBV)和平均通过时间(MTT)[2],这些血流动力学参数图可以为临床医生诊断提供重要辅助信息。CT血管造影技术和CT-MPI技术联合使用,不仅能提供冠状动脉狭窄的功能信息而且还能获得其狭窄部位的解剖结构信息[3]。根据扫描协议,CT-MPI对感兴趣层面连续多次增强扫描,和传统的CT扫描相比,这大大增加了病人所受的辐射剂量。大量研究表明,过高的X射线照射会诱发癌症,白血病或其他遗传性疾病[4]。当前,临床上采用的低剂量扫描方案虽然是一种降低辐射剂量简单易行的手段,但常常会导致所采集的投影数据受到量子噪声的影响,使得重建CT心肌灌注图像质量出现严重退化,从而影响诊断的精确度。因此,在保证一定图像质量的条件下,如何降低 CT-MPI中X射线辐射剂量已成为当前CT成像尤其是 CT-MPI领域最为重要的课题之一。
当前,针对CT-MPI剂量降低问题,除了采用心电门控技术和优化扫描模式,许多抑制图像噪声的方法相继被提出[5-8]。如Speidel等[5]在不考虑运动伪影的条件下采用HYPR技术恢复低剂量心肌灌注图像,该技术能在一定程度上抑制CT心肌灌注图像噪声。Ritman等[6]考虑了由心脏运动带来的运动伪影影响,利用多排探测器CT进行部分扫描重建的MPI研究,提出了一种基于目标的空间频率滤波策略,该策略能够减少因部分扫描引入的重建伪影。Tao等[7]将统计迭代(statistical iterative reconstruction,SIR)方法应用于CT-MPI,这种直接作用于投影数据的CT迭代重建方法能有效的抑制噪声和条行伪影;Bian等[8]提出了基于SIR的运动自适应稀疏先验算法应用于低剂量CT心肌灌注图像重建,该方法利用了CT心肌灌注图像的空间及时间结构的稀疏特性并将运动校正过程引入到迭代重建过程中,该方法在噪声消除,伪影抑制和细节保持方面均有良好效果。虽然上述方法能够获得优质的CT心肌灌注图像,但是这些方法在利用得到的CT心肌灌注图像估计血流动力学参数图时采用不稳定的截断奇异值分解去卷积方法。根据文献[9, 10],若要获得具有诊断意义的血流动力学参数图,必须采用鲁棒的灌注去卷积方法。因此,为了提高血流动力学参数图的估计精度,近年来许多灌注去卷积方法相继被提出[9, 10],Frindel等[9]构建了基于时空正则化去卷积模型应用于脑灌注加权MRI(perfusion-weighted magnetic resonance imaging,PW-MRI),并提出了全局收敛算法求解相应的目标函数。Fang等[10]提出基于全变分(TV)正则化去卷积方法应用于低剂量CT脑灌注成像,该方法能够有效改善脑血流动力学参数图。
受基于TV正则化去卷积模型启发,本文提出一种基于高维全变分(High dimension total variation,HDTV)正则化的CT 心肌灌注去卷积方法。其中,HDTV正则化利用了心肌血管空间结构相似性和心肌血流信号时间连续性。同时,针对新构建的CT-MPI去卷积目标函数的求解,本文提出一种改进的交替方向法优化策略。心肌灌注仿真数据和猪心肌灌注数据实验表明,与传统的去卷积方法[11-14]相比,本文方法能更有效地抑制低剂量血流动力学参数图中的噪声和伪影,同时较好地保持具有诊断意义的结构信息。
1 方法 1.1 CT灌注参数估计的去卷积法基于示踪剂稀释理论[13]和CT 灌注参数的计算模型[14-16],组织剩余函数R(t)计算方式如下:
| $C(t)\text{ }=MBF\text{ }\cdot {{C}_{a}}(t)*R(t)\text{ }=~{{C}_{a}}(t)*k(t)$ | (1) |
其中,∗为卷积算子符号,Ca(t)表示动脉对比剂浓度,也称之为动脉输入函数(arterial input function,AIF),C(t)表示组织内的对比剂浓度,k(t) =MBF ⋅R(t);(1)式中 C(t)和Ca(t)可从灌注数据直接测量获得,k(t)是未知的中间变量,MBF,MBV和MTT等灌注参数可以通过k(t)求得。根据文献[10, 14],卷积方程式(1)可被离散化为矩阵形式,对于感兴趣层面单个像素的卷积离散化矩阵表达式为:
| $Ak~=~c$ | (2) |
此时A ∈ℝN × N,N是采样次数,c ∈ℝN和k ∈ℝN。相对于(2)式,整个感兴趣层面的卷积离散化矩阵表达式为:
| $AK~=~C$ | (3) |
其中C = [c1……,cL] ∈ℝN× L ,K = [k1……,kL ∈ℝN × L,L表示感兴趣层面的像素个数。(1)式是基于这样的假设:对比剂到达AIF的时间不小于到达感兴趣层面组织的时间;实际中,我们测得的AIF并不一定是该组织的AIF,一般情况下AIF都会延迟于C(t),AIF和C(t)之间的时间漂移会导致计算的灌注参数不精确;为了避免对比剂延迟问题,许多研究提出了不同的解决方法[12, 17-18],其中 Wu等[12]采用块循环矩阵(Acirc)去卷积法效果较为显著,Acirc中的元素acirc可表示如下:
| ${{({{a}_{circ}})}_{i,j}}~=\left\{ \begin{align} & \Delta t{{c}_{art}}~\left( {{t}_{i\text{ }-\text{ }j\text{ }+\text{ }1}} \right)\text{ },for\text{ }j\text{ }\le \text{ }i \\ & \Delta t{{c}_{art}}~({{t}_{M+~i~-\text{ }j\text{ }+\text{ }1}})\text{ },for\text{ }j\text{ }>\text{ }i \\ \end{align} \right.~$ | (4) |
这里,Δt是数据采样时间间隔,i,j = 1,……N,M= 2N,矩阵K和C也要从N维扩展到M维,将(3)式替换为:
| $HX~=~Y$ | (5) |
此时H= Acirc,X ∈ℝM× L和Y ∈ℝM× L分别是对K和C补零扩展后的矩阵[14]。
1.2 基于HDTV正则化的去卷积模型关于(5)式的最小二乘解等价于极小化该式的二次欧几里得残差范数,可计算如下:
| ${{X}_{ls}}~=\text{ }\underset{K\text{ }\in {{\mathbb{R}}^{M\times ~L}}}{\mathop{argmin}}\,\text{ }~(||HX~-Y||\text{ }){{~}_{2}}^{2}~$ | (6) |
其中,H是一个病态的托普利茨矩阵,因此Xls并不是一个正定的最小二乘解,只要Y中微小的变化(投影噪声)就会导致Xls很大变动;为了得到优质的Xls,考虑到心肌血管空间结构相似性和心肌血流信号时间连续性,本文提出了基于HDTV正则化的去卷积模型,可表示为:
| ${{X}_{HDTV}}\text{ }=\text{ }\underset{X~\in {{\mathbb{R}}^{M\times ~L}}}{\mathop{argmin}}\,~\left( \frac{1}{2}||HX~-Y|{{|}_{2}}^{2}~+~\lambda \psi \left( X\text{ } \right) \right)$ | (7) |
其中,正则化项ψ(X)定义为
| $\psi \left( X\text{ } \right)\text{ }={{\left\| \sqrt{\underset{i=\text{ }0}{\overset{2}{\mathop{\Sigma }}}\,|{{\Phi }_{i}}^{T}~X{{\Psi }_{i}}{{|}^{2}}} \right\|}_{{{\ell }_{1}}}}~$ | (8) |
其中,Φ0 =Dx,Ψ0 = I,Φ1 =Dy,Ψ1 = I,Φ2 = I,Ψ2 =Dt;Dx,Dy和Dt是分别沿着x,y和t三维的有限差分算子;λ为正则化参数。
1.3 优化策略为了极小化(7)式,通过引入辅助变量S把(7)式转变成一个等价的约束问题,如下:
| $\begin{align} & \underset{X,S}{\mathop{min}}\,\text{ }\frac{1}{2}||HX~-Y|{{|}_{2}}^{2}~+~\lambda {{\left\| \sqrt{\underset{i=\text{ }0}{\overset{2}{\mathop{\Sigma }}}\,|{{S}_{i}}~{{|}^{2}}} \right\|}_{{{\ell }_{1}}}}~s.t.~{{S}_{i}}~ \\ & ={{\Phi }_{i}}^{T}~X{{\Psi }_{i}}~;~i~=\text{ }0,1,2 \\ \end{align}$ | (9) |
对于(9)式求解等价于极小化下面的增广拉格朗日函数[19]
| $\begin{align} & L\underset{X,S}{\mathop{(X,{{S}_{i}})}}\,\text{ }=\frac{1}{2}||HX~-Y||{{~}_{F}}^{2}~+~\lambda {{\left\| \sqrt{\underset{i=\text{ }0}{\overset{2}{\mathop{\Sigma }}}\,|{{S}_{i}}~{{|}^{2}}} \right\|}_{{{\ell }_{1}}}}+ \\ & \frac{\beta }{2}\text{ }\underset{i=\text{ }0}{\overset{2}{\mathop{\Sigma }}}\,\text{ }\left\| {{\Phi }_{i}}^{T}~X{{\Psi }_{i}} \right\|_{F}^{2}+\underset{0}{\overset{2}{\mathop{\Sigma }}}\,~\left\langle {{Z}_{i}},{{\Phi }_{i}}^{T}~X{{\Psi }_{i}}~-\text{ }S \right\rangle \\ \end{align}$ | (10) |
其中,Zi为拉格朗日乘子,β为惩罚参数,两个矩阵的内积定义为<A,B>= tr ace(AT B)。 我们使用交替极小化方法极小化(10)式,具体如下:
| ${{X}_{k\text{ }+\text{ }1}}~=\text{ }\underset{X}{\mathop{argmin}}\,\text{ }||HX~-Y||{{~}_{F}}^{2}~+\frac{\beta }{2}\text{ }\underset{i=\text{ }0}{\overset{2}{\mathop{\Sigma }}}\,\text{ }\left\| {{\Phi }_{i}}^{T}~X{{\Psi }_{i}} \right\|_{F}^{2}$ | (11) |
| $\begin{align} & {{S}_{k\text{ }+\text{ }1}}~=\text{ }\underset{\{{{S}_{i}}\}}{\mathop{argmin}}\,\frac{1}{2}\underset{i=\text{ }0}{\overset{2}{\mathop{\Sigma }}}\,\left\| \text{ }\left( {{\Phi }_{i}}^{T}~X{{\Psi }_{i}}~+~\frac{{{Z}_{k}}}{\beta } \right)-~{{S}_{i}} \right\| \\ & +~\frac{\lambda }{\beta }{{\left\| \sqrt{\underset{i=\text{ }0}{\overset{2}{\mathop{\Sigma }}}\,|{{S}_{i}}~{{|}^{2}}} \right\|}_{{{\ell }_{1}}}};~i~=\text{ }0,1,2 \\ \end{align}$ | (12) |
| ${{Z}_{i,k\text{ }+\text{ }1}}~=~{{Z}_{i,k}}~+\text{ }\left( \text{ }{{\Phi }_{i}}^{T}~X{{\Psi }_{i}}~-~{{S}_{i,k\text{ }+\text{ }1}}~ \right)\text{ };~i~=\text{ }0,1,2$ | (13) |
本文采用共轭梯度算法求解(11)式,(12)式的求解使用多维收缩算法[20]
| ${{S}_{k\text{ }+\text{ }1}}~=~\frac{{{P}_{i}}}{\underset{i=\text{ }0}{\overset{2}{\mathop{\Sigma }}}\,||~{{P}_{i}}~|{{|}^{2}}}{{\left( \underset{i=\text{ }0}{\overset{2}{\mathop{\Sigma }}}\,||~{{P}_{i}}~|{{|}^{2}}~-~\frac{\lambda }{\beta } \right)}_{+}}$ | (14) |
此时Pi = ΦiT XΨi + $\frac{{{Z}_{k}}}{\beta }$,(13)式是对拉格朗日乘子Zi的更新。
2 结果与讨论为了验证新方法在低剂量CT心肌灌注去卷积中的有效性,我们通过XCAT体模仿真和动物数据实验分别进行了定性分析和定量分析。
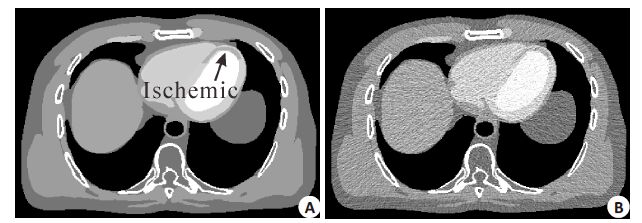
2.1 XCAT心肌灌注体模实验本实验中,选择修订的XCAT[21]体模仿真生成CT心肌灌注数据。CT仿真扫描的成像参数如下:XCAT体模图像大小为512×512,层厚为1 mm;射源到旋转中心和探测器的距离分别为746 mm和1361 mm;管电压为120 kVp,旋转角在[0,2π]间采样值为1160,探测器个数为672。低剂量投影数据生成方法参考文献[22-23],其中光子总数设为2.5×105,噪声方差σe2 = 10,最后对噪声测量数据进行FBP重建获得低剂量CT-MPI图像;为了体现本文方法对缺血心肌显示的优越性,我们通过临床医生指导在XCAT体模上定义了一块马蹄形缺血心肌区域;图 1给出了真值和低剂量仿真XCAT心肌灌注图像,其中黑色箭头所示为缺血心肌。
|
图 1 XCAT心肌灌注图像和低剂量仿真心肌灌注CT图像 Figure 1 XCAT myocardial perfusion image and low-dose image reconstructed from the simulated projection data. A: XCAT myocardial perfusion phantom; B: low-dose myocardial perfusion image reconstructed from the simulated projection data. |
为了定量分析不同方法的血流动力学参数图像质量,本文计算了标准参数图像与四种去卷积方法得到的参数图像之间的峰值信噪比(peak signal to noise ratio,PSNR)和相对均方根误差(relative root mean square error,rRMSE),其计算公式如下:
| $PSNR~=\text{ }10\text{ }log10\frac{MA{{X}^{2}}({{\mu }_{x\text{ }tr\text{ }ue}})}{\underset{n=\text{ }1}{\overset{Q}{\mathop{\Sigma }}}\,\left( \mu \left( n \right)\text{ }-~{{\mu }_{x\text{ }tr\text{ }ue}}~{{\left( n \right)}^{2}}/\left( Q-\text{ }1 \right) \right)}$ | (15) |
| $\begin{align} & PSNR~=\text{ }10\text{ }log10\frac{MA{{X}^{2}}({{\mu }_{x\text{ }tr\text{ }ue}})}{\underset{n=\text{ }1}{\overset{Q}{\mathop{\Sigma }}}\,\left( \mu \left( n \right)\text{ }-~{{\mu }_{x\text{ }tr\text{ }ue}}~{{\left( n \right)}^{2}}/\left( Q-\text{ }1 \right) \right)} \\ & rRMSE\text{ }=\sqrt{\frac{\underset{n=\text{ }1}{\overset{Q}{\mathop{\Sigma }}}\,{{\left( \mu \left( n \right)\text{ }-~{{\mu }_{x\text{ }tr\text{ }ue}}~\left( n \right) \right)}^{2}}}{\underset{n=\text{ }1}{\overset{Q}{\mathop{\Sigma }}}\,{{\left( {{\mu }_{x\text{ }tr\text{ }ue}}~\left( n \right) \right)}^{2}}}} \\ \end{align}$ | (16) |
μx tr ue表示标准参数图像,μ表示低剂量去卷积得到的参数图像,Q是感兴趣层面内的像素个数。
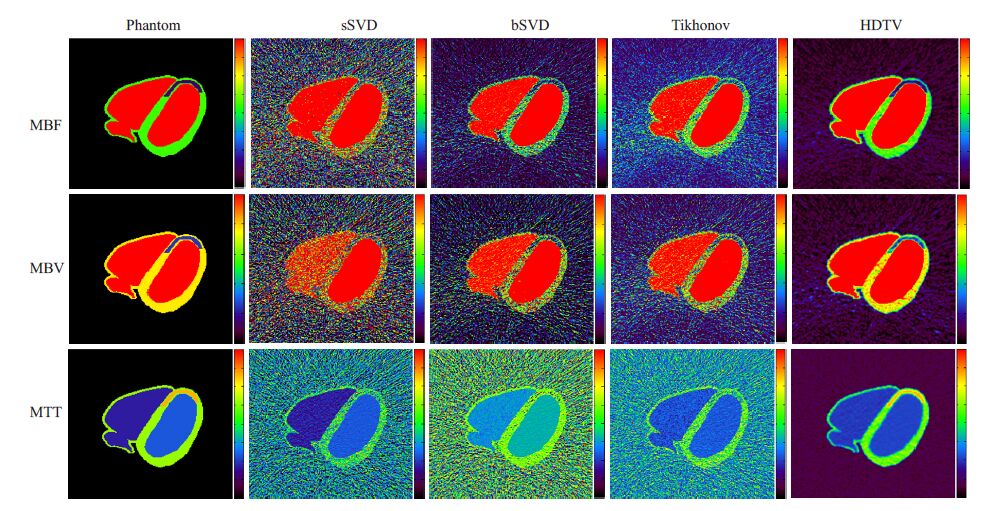
图 2所示为不同去卷积方法得到XCAT体模心肌灌注MBF,MBV和MTT血流动力学参数图像,其中这三种去卷积方法:标准截断奇异值分解(standard truncated singular value decomposition,sSVD)方法[11]、快循环矩阵截断奇异值分解(block-circulant truncated singular value decomposition,bSVD)方法[12]和Tikhonov正则化方法[14]目前广泛应用于商业灌注CT设备中。从图 2可以看出,由sSVD方法得到的三种参数图均含有严重的噪声和条形伪影,正常心肌和缺血心肌区域几乎被噪声淹没;bSVD和Tikhonov的结果稍有改善,但是与Phantom 参数图相比存在较大差距,且无法从其 MBF,MBV和MTT参数图像中分辨缺血心肌轮廓;本文方法结果明显优于其他三种方法,从MBF参数图中可以清晰的判断正常心肌和缺血心肌边界,进一步观察可以发现,本文方法得到的MBF,MBV和MTT参数图中背景区域和心脏区域条形伪影的抑制效果显著;通过与其他三种方法对比,本文方法降低噪声同时保持精确定量的参数图估计。图 3 分别对应于图 2 中的MBF,MBV和MTT的水平轮廓图(Profile)。相对于sSVD,bSVD和Tikhonov 方法,本文方法所得的轮廓图在心室,缺血心肌和健康心肌区域都更接近于体模参数图的轮廓图,继而说明本文方法能够实现低剂量CT-MPI血流动力学参数图的优质成像。
|
图 2 不同去卷积方法得到XCAT体模MBF、MBV、MTT血流动力学参数图 Figure 2 Hemodynamic parameter maps of the XCAT myocardial perfusion phantom by different methods. MBF in unit of mL·100 g-1·min-1,MBV in unit of mL/100 g,MTT in sec. |
|
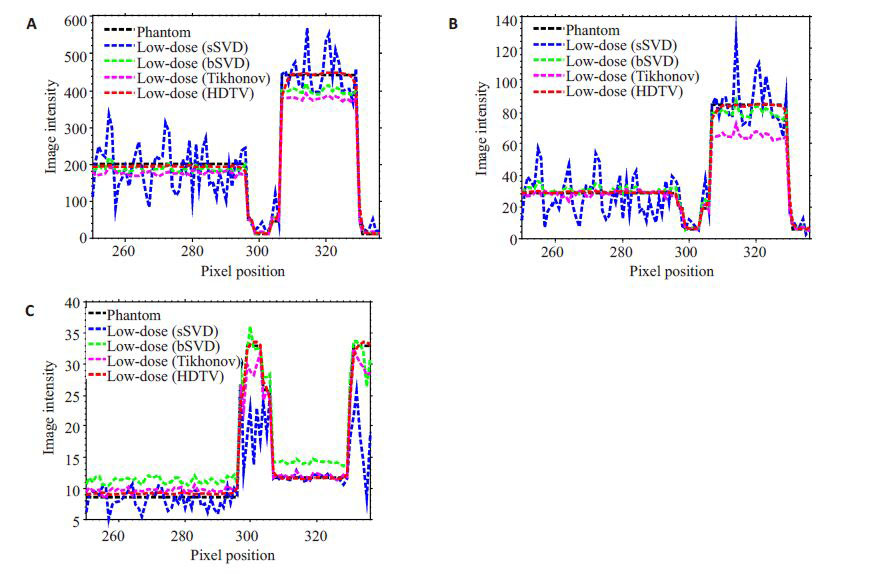
图 3 图 2中血流动力学参数图的水平轮廓图 Figure 3 Horizontal profiles (186 th row,250 th to336 th columns) of hemodynamic parameter maps in figure 2. A: Result from MBF; B: Result from MBV; C: Result from MTT. |
为了定量分析这4种方法的差异性,表 1列出了图 2中各参数图的PSNR和rRMSE测量值。由表 1可以看出,相对于sSVD,bSVD和Tikhonov方法,HDTV方法可以获得最高的PSNR测量值和最小的rRMSE测量值;尤其从MBF参数图的定量分析表明本文方法获得更高的PSNR和更低的rRMSE。
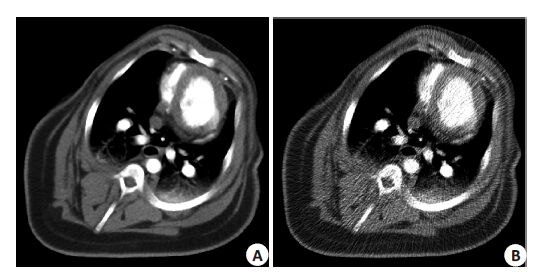
2.2 动物数据实验为进一步验证本文方法的有效性,我们对一组猪的 CT心肌灌注数据进行了测试。实验数据由GE公司 Discovery CT750 64层CT设备采集,射源到扫描物体和探测器的距离分别为538.52 mm和946.746 mm;管电压和管电流分别为120 kV,100 mA,层厚为5 mm,CT机架旋转一周时间为0.4 s;旋转角在[0,2π]间采样值为984,探测器个数888。为了减少辐射剂量避免二次扫描,根据文献[22-23],我们通过获得的高剂量心肌灌注数据仿真猪的低剂量心肌灌注数据。图 4给出了猪的高剂量和低剂量仿真心肌灌注图像。
|
图 4 高剂量和低剂量仿真猪心肌灌注 CT图像 Figure 4 Preclinical porcine high-dose myocardial perfusion image and low-dose image reconstructed from the simulated projection data. A: Highdose CT-MP image reconstructed by the FBP; B: Low-dose CT-MP image reconstructed by FBP. |
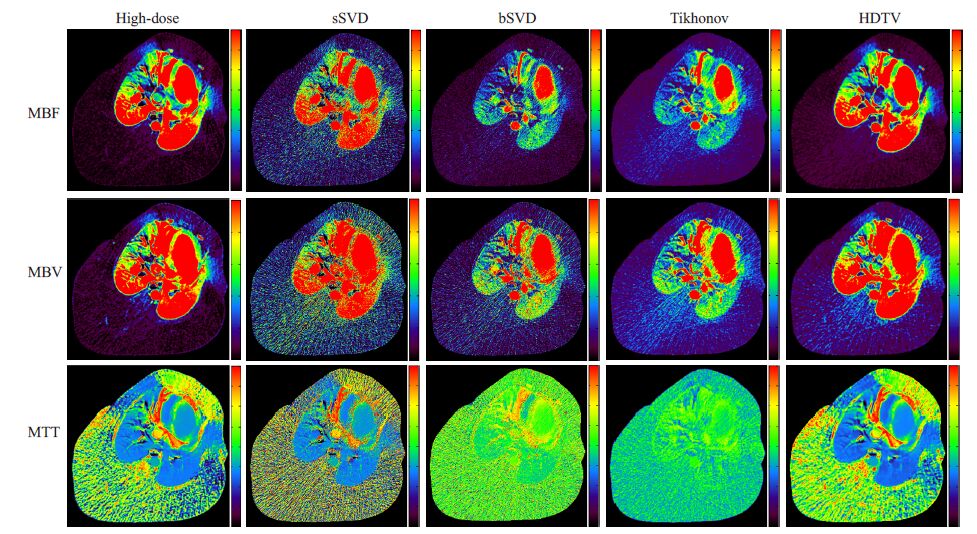
图 5显示了不同方法计算的心肌血流动力学参数图。由图 5可以看出,本文提出的HDTV正则化去卷积方法抑制了噪声和伪影的同时保持了清晰的细节。从 MBF参数图可以看出本文方法估计的MBF和高剂量得到的MBF 具有高度一致性,而sSVD,bSVD 和 Tikhonov方法获得的MTT参数图严重退化。基于奇异值分解的Tikhonov方法获得的三种参数图在噪声较少和条行伪影抑制方面有一定的改善,但是通过总体对比,本文方法在噪声滤除和边缘细节保持两方面表现更为突出。表 2所示为图 5中各参数图的PSNR和rRMSE测量值,可以看出,本文方法较其他方法在真实动物数据实验中具有更好的噪声抑制性能。
|
图 5 不同去卷积方法得到猪的MBF、MBV、MTT血流动力学参数图 Figure 5 Hemodynamic parameter maps of pig myocardial perfusion image by different methods. MBF in unit of mL/100 g/min,MBV in unit of mL/100 g,and MTT in sec. |
针对低剂量CT心肌灌注去卷积估计动力学参数不准确问题,本文提出一种基于HDTV正则化的去卷积方法,其中,HDTV正则化利用心肌血管空间结构相似性和心肌血流信号时间连续性。为了评价本文方法的优异性,我们采用XCAT仿真和猪心肌灌注数据进行实验。通过与SVD、bSVD和Tikhonov 去卷积方法实验结果对比,本文方法实验结果表明能有效抑制心肌血流动力学参数图噪声和伪影,且本文方法的实验结果更加逼近XCAT 真值参数图和高剂量猪参数图。我们从 MBF,MBV和MTT参数图可以清晰判断出缺血心肌的位置和大小,这对于临床有实际的应用意义。
由于算法引入惩罚参数λ来平衡保真项和正则化项,本文未对λ进行自适应优化设计,而是通过去卷积过程的视觉评价,因此存在一定的缺陷;另外,本文仅列出了三种商业软件广泛使用去卷积方法作为对比,还有其他重建和图像后处理方法需要进一步的对比试验;还有本文实验基于XCAT体模仿真和动物实验,若要实现本文方法的临床应用,还需要进行更为广泛的临床实验。
| [1] | Becker A, Becker C. CT imaging of myocardial perfusion: possi- bilities and perspective[J]. J Nucl Cardiol,2013, 20 (2) : 289-96. DOI: 10.1007/s12350-013-9681-7. |
| [2] | George RT, Jerosch-Herold M, Silva C, et al. Quantification of myocardial perfusion using dynamic 64-detector computed tomo- graphy[J]. Invest Radiol,2007, 42 (12) : 815-22. DOI: 10.1097/RLI.0b013e318124a884. |
| [3] | Mehra VC, Ambrose M, Valdiviezo-Schlomp C, et al. CT-based myocardial perfusion imaging-practical considerations: acquisition, image analysis, interpretation, and challenges[J]. J Cardiovasc Transl Res,2011, 4 (4) : 437-48. DOI: 10.1007/s12265-011-9286-y. |
| [4] | Brenner DJ, Hall EJ. Computed tomography-an increasing source of radiation exposure[J]. N Engl J Med,2007, 357 (22) : 2277-84. DOI: 10.1056/NEJMra072149. |
| [5] | Speidel MA, Bateman CL, Tao Y, et al. Reduction of image noise in low tube current dynamic CT myocardial perfusion imaging using HYPR processing: a time-attenuation curve analysis[J]. Med Phys,2013, 40 (1) : 011904. DOI: 10.1118/1.4770283. |
| [6] | Ramirez-Giraldo JC, Yu L, Kantor B, et al. A strategy to decrease partial scan Reconstruction artifacts in myocardial perfusion CT: phantom and in vivo evaluation[J]. Med Phys,2012, 39 (1) : 214-23. DOI: 10.1118/1.3665767. |
| [7] | Tao Y, Chen GH, Hacker TA, et al. Low dose dynamic CT myocardial perfusion imaging using a statistical iterative Reco- nstruction method[J]. Med Phys,2014, 41 (7) : 071914. DOI: 10.1118/1.4884023. |
| [8] | Biao ZY, Gong CF, Zeng D, et al. Motion Adaptive Sparsity Prior for Low-dose Dynamic CT Myocardial Perfusion Imaging[D]. The 13th International Meeting on Fully Three-Dimensional, 2015. |
| [9] | Frindel C, Robini MC, Rousseau D. A 3-D spatio-temporal deco-nvolution approach for Mr perfusion in the brain[J]. Med Image Anal,2014, 18 (1) : 144-60. DOI: 10.1016/j.media.2013.10.004. |
| [10] | Fang R, Zhang S. Chen T, et al. Robust low-dose CT perfusion deconvolution via tensor total-variation regularization[J]. IEEE Trans Med Imaging, 2015, Feb 20.[Epub ahead of print] |
| [11] | Ostergaard L, Weisskoff RM, Chesler D, et al. High resolution measurement of cerebral blood flow using intravascular tracer bolus passages. Part I: Mathematical approach and statistical analysi[J]. Magn Reson Med,1996, 36 (5) : 715-25. DOI: 10.1002/(ISSN)1522-2594. |
| [12] | Wu O, Ostergaard L, Weisskoff RM, et al. Tracer arrival timing- insensitive technique for estimating flow in Mr perfusion-weighted imaging using singular value decomposition with a block-circulant deconvolution matrix[J]. Magn Reson Med,2003, 50 (1) : 164-74. DOI: 10.1002/mrm.v50:1. |
| [13] | Zierler K. Indicator dilution methods for measuring blood flow, volume, and other properties of biological systems: a brief history and memoi[J]. Ann Biomed Eng,2000, 28 (8) : 836-48. DOI: 10.1114/1.1308496. |
| [14] | Fieselmann A, Kowarschik M, Ganguly A, et al. Deconvolution- based CT and MR brain perfusion measurement: theoretical model revisited and practical implementation details[J]. Int J Biomed Imaging,2011 : 467563. |
| [15] | Fahmi R, Eck BL, Vembar M, et al. Dynamic CT myocardial perfusion imaging: detection of ischemia in a porcine model with FFR verification[J]. Proc SPIE,2014 : 9038. |
| [16] | Fahmia R, Eck BL, Vembar M, et al. Dose reduction assessment in dynamic CT myocardial perfusion imaging in a porcine balloon- induced-ischemia mode[J]. Proc SPIE Med Imaging,2014 : 9033. |
| [17] | Calamante F, Gadian GD, Connelly A. Delay and dispersion effects in dynamic susceptibility contrast mri: simulations using singular value decomposition[J]. Magn Reson Med,2000, 44 (3) : 466-73. DOI: 10.1002/(ISSN)1522-2594. |
| [18] | Mouannes-Srour JJ, Shin W, Ansari SA, et al. Correction for arterial-tissue delay and dispersion in absolute quantitative cerebral perfusion DSC Mr imaging[J]. Mag Reson Med,2012, 68 (2) : 495-506. DOI: 10.1002/mrm.23257. |
| [19] | Hestenes M. Multiplier and gradient methods[J]. J Optim Theo Appl,1969, 4 (1) : 303-20. |
| [20] | Yang J, Zhang Y. Alternating direction algorithms for L1-problems in compressive sensing[J]. SIAM J Sci Comput,2011, 33 (1) : 250-78. DOI: 10.1137/090777761. |
| [21] | Segars WP, Sturgeon G, Mendonca S, et al. 4D XCAT phantom for multimodality imaging research[J]. Med Phys,2010, 37 (9) : 4902-15. DOI: 10.1118/1.3480985. |
| [22] | Ma JH, Liang ZR, Fan Y, et al. Variance analysis of x-ray CT sinograms in the presence of electronic noise background[J]. Med Phys,2012, 39 (7) : 4051-65. DOI: 10.1118/1.4722751. |
| [23] | Ma J, Zhang H, Gao Y, et al. Iterative image Reconstruction for cerebral perfusion CT using a pre-contrast scan induced edge- preserving prio[J]. Phys Med Biol,2012, 57 (22) : 7519-42. DOI: 10.1088/0031-9155/57/22/7519. |
 2015, Vol. 35
2015, Vol. 35

