2. 烟台毓璜顶医院核医学科,山东 烟台 264000 ;
3. 广东省人民医院//广东省医学科学院肿瘤中心放疗科,广东 广州 510080
2. Department of Nuclear Medicine, Yantai Yuhuangding Hospital, Yantai 264000, China ;
3. Department of Radiology, Cancer Center, Guangdong General Hospital/Guangdong Academy of Medical Science, Guangzhou 510080, China
与传统的SPECT心肌成像相比,PET心肌灌注成像可以提高诊断准确性,更好地确认病灶位置,还能定量分析心脏血流[1-2]。尤其是PET动态心肌灌注成像还能测量心肌区域放射性药物的生物分布[3-4],这就使得估计动力学参数[例如示踪剂输送速率参数K1和心肌血流量(MBF)]变得非常有意义。然而,PET动态心肌灌注成像主要还处于研究阶段,临床上还缺乏应用。主要的问题是将数据细分到短帧时,会带入噪声,从而影响心肌绝对血流的定量。传统上,标准的动态PET成像由单独的帧独立重建得到,然后在体素或ROI水平上运用动力学模型得到时间活度曲线(TAC)。独立图像重建主要靠统计图像重建方法实现,例如最大似然期望值法(MLEM)[5]。然而,当在低计数情况下,直接采用MLEM算法方差很大[6]。而且方差还会随着采样间隔的增大而增大。有人提出利用PET图像的稀疏特性的重建算法[7]。例如在PET动态图像重建中加入全变分正则约束。这种方法不论是在图像空间[8-9],还是在测度空间[10]上都得到了应用。另外多维小波去噪可以恢复隐藏在动态PET图像中的生物信号保真度,从而准确的定量心肌灌注。学者Su和Shoghi在2008提出小波降噪技术[11],它对噪声敏感度低,在高噪声水平下可以提供更加准确的参数估计。
最近,有研究者提出了利用矩阵的低秩性质恢复图像。该研究首先在动态核磁共振成像[12-13]上受到关注,学者Lingala等[14-15]将其与稀疏先验结合分别运用到磁共振图像的恢复和重建上。在动态PET心肌灌注成像上,连续的图像之间有高度相关的冗余信息,这使得图像矩阵有很好的低秩性。另外在图像某些部分,含有血流灌注信息,这部分是稀疏的。因此,本文在动态PET心肌灌注成像上提出一种结合低秩与稀疏惩罚的重建方法(L & S)。我们利用split Bregman算法求解凸最优化问题,并利用真实的PET心肌82Rb灌注成像来最优化正则化参数。我们在成像视觉上和信噪比上对L & S方法做了评估。同时我们将该算法与传统的MLEM算法以及单独利用稀疏或低秩惩罚的算法进行了比较。
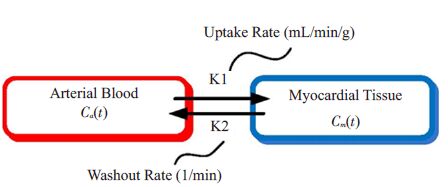
1 材料和方法 1.1 动态82RbPET心肌灌注仿真数据在我们的仿真研究中,我们选用单房室模型,如图 1所示,其中K1( mL/min/g),k2( 1/min)为2个标准的动力学参数。左边红色框内的是动脉血,右边蓝色框内的是心肌组织,放射示踪物以K1的速率从动脉血进入心肌组织,并以反馈速率k2从心肌组织流回动脉血[16-17]。
|
图 1 动态82RbPET心肌灌注单房室模型 Figure 1 One-tissue compartment model for kinetic modeling of82Rb MP PET imaging. |
这两个速率常数与动脉和心肌组织中的放射性活度成线性相关。动态过程可以通过如下方程描述:
| $\frac{d{{C}_{m}}\left( t \right)}{dt}={{K}_{1}}{{C}_{a}}\left( t \right)-{{K}_{2}}{{C}_{m}}\left( t \right)$ | (1) |
其中Ca(t)和Cm(t)分别是动脉血和心肌中82Rb的浓度。通过测定左心室(LV)中心一小区域的82Rb的浓度获得CLV (t),这是一种非侵入方法,几乎可以完全恢复动脉输入曲线,并最大限度减少心肌溢出(Ca(t) = CLV (t))。而且,如果定义Fa为组织中的血浆体积分数,那么心肌中的放射示踪物浓度可以表示成:
| $C\left( t \right)={{F}_{a}}{{C}_{a}}\left( t \right)+\left( 1-{{F}_{a}} \right){{C}_{m}}\left( t \right)$ | (2) |
其中,Fa是0至1之间的实数,代表整个血液中的体积分数,包括:
(a) 由于PET采样时的部分容积效应从血池进入心肌的
(b) 肌肉中的动脉血
对方程(1)和(2)求解可以得到如下结果:
| $C\left( t \right)={{F}_{a}}{{C}_{a}}\left( t \right)+\left( 1-{{F}_{a}} \right){{K}_{1}}{{e}^{-{{k}_{2}}t}}\otimes {{C}_{a}}\left( t \right)$ | (3) |
其中,⊗是卷积算子。
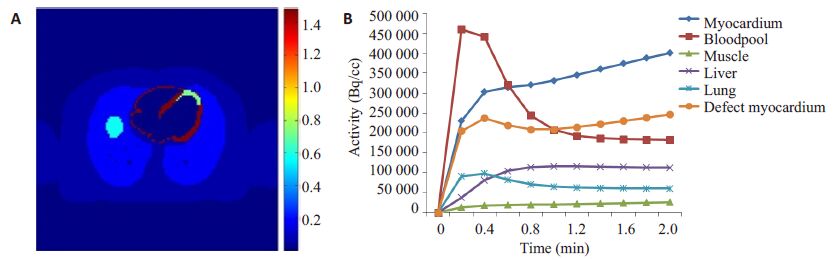
首先为多个区域(心肌,肺等)各自估计K1,k2常数和Fa,然后求其平均值。动脉血放射示踪物浓度Ca(t)通过计算动脉血采样的平均值得到。利用XCAT体模[18],根据(3)式便可以生成一套动态PET心肌灌注图像。如图 2所示,图 2A给出了K1参数图像,图 2B为采用单房室模型产生的时间活度曲线(TAC)。我们在2 min内采样10帧(10×12 s),这是心肌灌注PET成像的常规采样协议。
|
图 2 K1参数图像和采用单房室模型产生的时间活度曲线(TAC) Figure 2 K1 parametric image(A)and TACs generated using one-tissue compartmentalmodel(B) |
我们仿真了GE的RX PET/CT scanner 型号扫描器[19]。仿真器产生无噪声投影数据,该数据经过放大,添加泊松噪声达到真实的临床噪声水平。仿真过程考虑了衰减,正则化的影响,这些影响都包含入了再重建过程。将得到的数据分别采用MLEM、低秩惩罚、稀疏惩罚和L & S四种方法重建。其中MLEM算法,经过63次迭代得到(等于用OSME算法,21个子集,3次迭代重建[19])的动态图像是128 × 128 × 47的三维矩阵,体像素大小为3.27 mm× 3.27 mm× 3.27 mm。
1.3 低秩矩阵的恢复将低秩矩阵X从观测矩阵M恢复的问题,如(4)式所示,其中M是包含误差E的矩阵(M= X + E)。
| $\underset{X}{\mathop{\min }}\,\frac{1}{2}//X-M//_{F}^{2}+\lambda rank\left( X \right)$ | (4) |
其中rank(X)代表矩阵X的秩,∥⋅∥ F为F-范数,λ是超参数,用来平衡第一项(保真项)和第二项(惩罚项)。直接求(4)式中目标函数的极小值是很困难的,因为里面包含秩惩罚。为了简化计算,将秩惩罚用核范数∥X ∥ *表示,
| $//X//*=\sum\limits_{i}{{{\sigma }_{i}}}$ | (5) |
其中σi是矩阵X的奇异值。经过这样的松弛处理,低秩矩阵X的恢复可以简化为:
| $\underset{X}{\mathop{\min }}\,\frac{1}{2}//X-M//_{F}^{2}+\lambda //\left( X \right)//*$ | (6) |
对于PET动态心肌灌注成像,令xt表示第t帧图像的示踪剂活度,t = 1,2,...T,T是动态图像总帧数,xjt表示第t帧第j个体素的示踪剂活度,j = 1,2,...N,N为体素的总个数。由此,我们可以构造矩阵:
| $X=\left( \begin{matrix} x_{1}^{1} & x_{1}^{2} & \cdots & x_{1}^{T} \\ x_{2}^{1} & x_{2}^{2} & \cdots & x_{2}^{T} \\ \vdots & \vdots & \ddots & \vdots \\ x_{N}^{1} & x_{N}^{2} & \cdots & x_{N}^{T} \\ \end{matrix} \right)$ | (7) |
其中,X ∈RN × T代表所有的动态帧图像。矩阵X的每一列表示相应帧图像的示踪剂活度,每一行表示对应体素的时间活度曲线(TAC)。矩阵X实际上是背景部分和动态部分的叠加。背景部分代表帧或区域之间高度相关的部分(例如肌肉组织和肺),这部分的示踪剂活度随时间变化缓慢,可以将其看作低秩部分(L)。动态部分代表帧或区域之间变化的部分(例如心肌和血池),这部分的示踪剂活度随时间快速变化,是稀疏的(S)。因此我们在动态PET心肌灌注成像上同时引入低秩和稀疏惩罚,即L & S模型。求解过程可以表示成对一个凸优化问题的求解[14-15]。
| $\underset{X}{\mathop{\min }}\,\frac{1}{2}//X-M//_{F}^{2}+{{\mu }_{L}}\phi \left( X \right)+{{\mu }_{s}}\varphi \left( X \right)$ | (8) |
其中,μL 和μs 是相关的正则化参数,ϕ(X)是是谱惩罚项,将其用p-范数表示,定义为ϕ(X) =${{\left( \sum\limits_{i}{\sigma _{i}^{p}} \right)}^{\frac{1}{p}}}$,用来惩罚小的奇异值。当p < 1时,该惩罚项为非凸的范数,例如Lingala 选择P=0.1 的谱惩罚[14]。这里,我们选择p = 1,将其简化为核范数。φ(X)定义表示时间空间的全变分项,也就是矩阵在x,y,t方向的梯度的1-范数,通过有限差分估计,定义如下:
| $\varphi \left( X \right)={{\left\| {{\left( \sum\nolimits_{i=1}^{2}{{{\left| \Phi _{i}^{T} \right|}^{2}}} \right)}^{\frac{1}{2}}} \right\|}_{1}}$ | (9) |
其中,Φ0 =Dx,Φ1 =Dy,Φ2 = I
本文采用split Bregman法[20-21]来最优化(8)式中的代价函数,它本质上来说是一种增广拉格朗日法。(8)式中代价函数的求解可以通过下列迭代实现:
| $\begin{align} & {{X}^{k+1}}=\arg \min \left\| X-M+{{Z}^{k}} \right\|_{F}^{2}+{{\beta }_{1}}\left\| X-{{E}^{k}} \right\|_{F}^{2}+ \\ & {{\beta }_{2}}\sum\nolimits_{i=0}^{2}{\left\| \Phi _{i}^{T}X{{\Psi }_{i}}-S_{i}^{k}+V_{i}^{k} \right\|}_{F}^{2} \\ \end{align}$ | (10) |
| ${{E}^{k+1}}=\arg \min \left\| {{X}^{k+1}}+{{L}^{k}}-E \right\|_{F}^{2}+2{{\mu }_{L}}/{{\beta }_{1}}{{\left\| E \right\|}_{*}}$ | (11) |
| ${{S}^{k+1}}=\arg \min \sum\nolimits_{i=0}^{2}{\left\| \Phi _{i}^{T}{{X}^{k+1}}{{\Psi }_{i}}-{{S}_{i}}+V_{i}^{k} \right\|}_{F}^{2}$ | (12) |
| ${{L}^{k+1}}={{L}^{k}}+{{X}^{k+1}}+{{E}^{k+1}}$ | (13) |
| $V_{i}^{k+1}=V_{i}^{k}+\Phi _{i}^{T}{{X}^{k+1}}{{\Psi }_{i}}-S_{i}^{k+1};i=1,1,2.$ | (14) |
| ${{Z}^{k+1}}={{Z}^{k}}+{{X}^{k+1}}+M$ | (15) |
为比较前面提到的不同重建方法的效果,我们比较了定量评价标准。均方误差定义为:
| $MS{{E}_{ROI}}=Bias_{ROI}^{2}+\text{Va}{{\text{r}}_{ROI}}$ | (16) |
其中,
| $Bias_{ROI}^{2}=\frac{\sum\nolimits_{j=1}^{N}{{{\left( {{{\bar{x}}}_{j}}-x_{j}^{\text{tr ue}} \right)}^{2}}}}{\sum\nolimits_{j=1}^{N}{{{\left( x_{j}^{\text{tr ue}} \right)}^{2}}}}$ | (17) |
| $\text{Va}{{\text{r}}_{ROI}}=\frac{1}{R}\frac{\sum\nolimits_{r=1}^{R}{\sum\nolimits_{j=1}^{N}{{{\left( \bar{x}_{j}^{r}-{{{\bar{x}}}_{j}} \right)}^{2}}}}}{\sum\nolimits_{j=1}^{N}{{{\left( x_{j}^{\text{tr ue}} \right)}^{2}}}}$ | (18) |
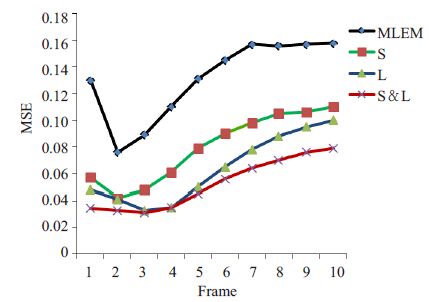
R是方差实现的总数(我们的仿真中R=30),N是ROI中的体素个数,${{{\bar{x}}}_{j}}=\frac{1}{R}\sum\nolimits_{r=1}^{R}{x_{j}^{r}}$代表PET图像在第j个体素点的总平均值,xjr代表在指定ROI第j 个体素经过r 次重建,xjtr ue 代表参考组中第j 个体素点的真实的PET图像值。为了比较不同重建算法的性能,对每一帧动态图像计算其均方误差(MSE),如图 3所示,横坐标是帧,纵坐标是每个重建算法对应的帧的MSE。从图中可以明显地看出MLEM方法每一帧图像的MSE值都明显大于其它3种算法。采用低秩惩罚(L)重建的图像的MSE 要小于采用稀疏惩罚(S)重建的图像的MSE。我们提出的L & S方法重建的图像的MSE是所有方法中最小的。
|
图 3 不同重建算法对应帧的MSE Figure 3 Plots of MSE vs frame number for reconstructedimages by MLEM (black),sparse penalty(green),Lowrank penalty (blue) and L & S (red) algorithm. |
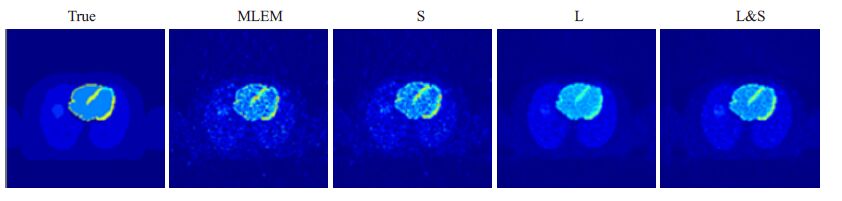
为了提供直接视觉比较,图 4是给出了上述4种算法重建的图像。这些图像是4D动态PET心肌图像第26 层断层图像的第10 帧。从图中可以清楚地看到MLEM算法与稀疏惩罚(S)大幅增加了噪声水平,低秩惩罚(L)和L & S方法明显降低了噪声水平。与低秩惩罚(L)重建相比,L & S重建保留了更多图像特征。
|
图 4 从左到右依次是真实图像(True)以及通过MLEM,稀疏惩罚(S)、低秩惩罚(L)和L & S重建得到的图像 Figure 4 Raw image and reconstructed images by MLEM,sparse penalty,low rank penalty and L & S algorithm. |
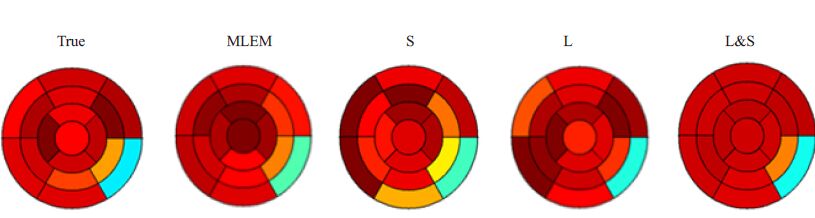
此外,为了评价心肌缺损,我们还生成了左心室靶心图[22]。我们采用美国心脏协会的17段模型,它更适合评价室壁运动和心肌灌注[23]。图 5显示了不同重建算法得到的第10帧图像的17段靶心图。通过比较,我们可以发现L & S方法生成的靶心图的和参考组的真实靶心图最相近。我们可以清楚地看到与其它重建方法相比,L & S重建图像的靶心图无论是在正常心肌区域的还是缺损部分,与参考靶心图的偏差都最小。
|
图 5 从左到右依次是真实图像(True)的靶心图以及通过MLEM,稀疏惩罚(S)、低秩惩罚(L)和L & S算法重建得到的图像的靶心图 Figure 5 Polar map of the raw image and reconstructed images by MLEM,sparse penalty,Low rank penalty and L & Salgorithm. All the polar maps were shown in the same color bar. |
本文提出了一种结合低秩与稀疏惩罚的(L & S)动态PET心肌灌注图像的重建方法。该方法可以表述为一个凸最优化问题。我们采用split Bregman 算法求解这个问题。我们用单房室模型仿真了一套动态PET心肌灌注图像,利用真实的动态PET心肌灌注成像来最优化正则化参数。本文提出的L & S重建算法得到的每帧动态图像的MSE是前面提到的算法中最小的。L & S重建不仅降低了图像噪声,而且保留了更多图像特征。此外比较不同算法重建的图像的靶心图,可以发现L & S方法生成的靶心图的灰度值和参考组的真实靶心图最相近,无论是在正常心肌区域的还是缺损部分,与参考靶心图的偏差都最小。
总之,我们提出的L & S重建算法得到的图像,无论是在直观视觉上,还是定量分析上都优于另外3种方法。
| [1] | Sampson UK, Dorbala S, Limaye A, et al. Diagnostic accuracy of rubidium-82 myocardial perfusion imaging with hybrid positron emission tomography/computed tomography in the detection of coronary artery disease[J]. J Am Coll Cardiol,2007, 49 (10) : 1052-8. DOI: 10.1016/j.jacc.2006.12.015. |
| [2] | Bateman TM, Heller GV, Mcghie AI, et al. Diagnostic accuracy of rest/stress ECG-gated Rb-82 myocardial perfusion PET: comparison with ECG-gated Tc-99m sestamibi SPECT[J]. J Nucl Cardiol,2006, 13 (1) : 24-33. DOI: 10.1016/j.nuclcard.2005.12.004. |
| [3] | Coxson PG, Huesman RH, Borland L. Consequences of using a simplified kinetic model for dynamic PET data[J]. J Nucl Med,1997, 38 (4) : 660-7. |
| [4] | El Fakhri G, Sitek A, Guérin B, et al. Quantitative dynamic cardiac 82Rb PET using generalized factor and compartment analyses[J]. J Nucl Med,2005, 46 (8) : 1264-71. |
| [5] | Mumcuo?lu EU, Leahy RM, Cherry SR. Bayesian Reconstruction of PET images: methodology and performance analysis[J]. Phys Med Biol,1996, 41 (9) : 1777-807. DOI: 10.1088/0031-9155/41/9/015. |
| [6] | Reader AJ, Zaidi H. Advances in PET image Reconstruction[J]. PET Clin,2007, 2 (2) : 173-90. DOI: 10.1016/j.cpet.2007.08.001. |
| [7] | Shidahara M, Ikoma Y, Kershaw J, et al. PET kinetic analysis: wavelet denoising of dynamic PET data with application to parametric imaging[J]. Ann Nucl Med,2007, 21 (7) : 379-86. DOI: 10.1007/s12149-007-0044-9. |
| [8] | Wang CY, Hu ZH, Shi PC, et al. Low dose PET Reconstruction with total variation regularization[C]//2014 36TH Annual international conference of the ieee engineering in medicine and biology society (EMBC), 2014: 1917-20. |
| [9] | Mehranian A, Rahmim A, Ay MR, et al. An ordered-subsets proximal preconditioned gradient algorithm for total variation regularized PET image Reconstruction [C]//Nuclear Science Symposium and Medical Imaging Conference, 2012: 3375-82. |
| [10] | Burger M, Mueller J, Papoutsellis E, et al. Total variation regularization in measurement and image space for PET Reconstruction[J]. Inverse Probl,2014, 30 (10) : 105003. DOI: 10.1088/0266-5611/30/10/105003. |
| [11] | Su Y, Shoghi KI. Wavelet denoising in voxel-based parametric estimation of small animal PET images: a systematic evaluation of spatial constraints and noise reduction algorithms[J]. Phys Med Biol,2008, 53 (21) : 5899-915. DOI: 10.1088/0031-9155/53/21/001. |
| [12] | Zhao B, Haldar JP, Brinegar C, et al. Low rank matrix recovery for real-time cardiac mri[C]//2010 7TH ieee international symposium on biomedical imaging: From Nano To Macro, 2010: 996-9. |
| [13] | Haldar JP, Liang ZP. Spatiotemporal imaging with partially separable functions: a matrix recovery approach[C]//2010 7TH ieee international symposium on biomedical imaging: From Nano To Macro, 2010: 716-9. |
| [14] | Lingala SG, Hu Y, Dibella E, et al. Accelerated dynamic MRI exploiting sparsity and low-rank structure: k-t SLR[J]. IEEE Trans Med Imaging,2011, 30 (5) : 1042-54. DOI: 10.1109/TMI.2010.2100850. |
| [15] | Zhao B, Haldar JP, Christodoulou AG, et al. Image Reconstruction from highly undersampled (k, t)-space data with joint partial separability and sparsity constraints[J]. IEEE Trans Med Imaging,2012, 31 (9) : 1809-20. DOI: 10.1109/TMI.2012.2203921. |
| [16] | Rahmim A, Tang J, Mohy-Ud-Din H. Direct 4D parametric imaging in dynamic myocardial perfusion PET[J]. Frontiers in Biomedical Technologies,2014, 1 (1) : 4-13. |
| [17] | Mohy-Ud-Din H, Karakatsanis NA, Lodge MA, et al. Parametric myocardial perfusion PET imaging using physiological clustering [C]. Proc of Spie, 2014, 9038: 1-11. |
| [18] | Segars WP, Mahesh M, Beck TJ, et al. Realistic CT simulation using the 4D XCAT phantom[J]. Med Phys,2008, 35 (8) : 3800-8. DOI: 10.1118/1.2955743. |
| [19] | Kemp BJ, Kim C, Williams JJ, et al. NEMA NU 2-2001 performance measurements of an LYSO-based PET/CT system in 2D and 3D acquisition modes[J]. J Nucl Med,2006, 47 (12) : 1960-7. |
| [20] | Osher S, Burger M, Goldfarb D, et al. An iterative regularization method for total variation-based image restoration[J]. Multiscale Modeling Simulation,2005, 4 (2) : 460-89. DOI: 10.1137/040605412. |
| [21] | Goldstein T, Osher S. The split bregman method for L1-Regularized problems[J]. SIAM J Imaging Sci,2009, 2 (2) : 323-43. DOI: 10.1137/080725891. |
| [22] | Cerqueira MD, Weissman NJ, Dilsizian V, et al. Standardized myocardial segmentation and nomenclature for tomographic imaging of the heart. A statement for healthcare professionals from the Cardiac Imaging Committee of the Council on Clinical Cardiology of the American Heart Association[J]. Circulation,2002, 105 (4) : 539-42. DOI: 10.1161/hc0402.102975. |
| [23] | Lin GS, Hines HH, Grant G, et al. Automated quantification of myocardial ischemia and wall motion defects by use of cardiac SPECT polar mapping and 4-dimensional surface rendering[J]. J Nucl Med Technol,2006, 34 (1) : 3-17. |
 2015, Vol. 35
2015, Vol. 35

