2. 南方医科大学生物医学工程学院,广东 广州 510515
2. School of Biomedical Engineering, Southern Medical University, Guangzhou 510515, China
环形伪影是X-线计算机断层成像常见的一种伪影,其产生的因素有很多,主要包括探测器的探测单元存在故障,探测单元没有校正,探测器上存在着灰尘和杂质等[1-2]。环形伪影在CT 图像中主要表现为一系列同心圆环或者圆弧,其在线积分投影数据上表现为竖直方向上的直线[3]。环形伪影在一定程度上降低图像质量,给图像噪声处理及图像分割等后续处理带来很大困扰,严重影响影像诊断效果。因此,去除或者最大程度地减少环形伪影是十分必要的。
目前,大量的环形伪影去除方法相继被提出[2, 4-11],主要分为两类,一类是基于线积分投影数据的去除方法,即图像重建前的处理方法。例如,Boin 等[4]采用均值滤波方法去除原始数据中因探测器响应不一致带来的高频信号,该方法可以有效抑制环形伪影,但图像分辨率会略有下降;余晓锷等[5]采用Hough 变换对线积分投影数据中的环形伪影进行准确定位,继而对相应位置上的数据进行线性插值实现校正;Münch 等[6]对线积分投影数据进行小波变换,利用低通滤波方法滤除垂直方向的高频分量,可以实现弱强度环形伪影的去除。第二类是基于CT 重建图像的去除方法,是一种图像后处理方法[2, 8-11]。该类方法的主要思想是,将CT 图像通过坐标变换,将图像从直角坐标系变换到极坐标,在极坐标下对变换后的数据进行滤波处理,去除条形伪影,最后将处理后的数据再经过坐标变换回到直角坐标系。此类方法需经过两次坐标变换,若滤波器的阈值设置不妥当,将导致图像对比度和分辨率的明显下降。
针对上述两类方法各自的不足,本文提出一种基于投影域小波变换的环形伪影去除方法,此方法把线积分投影数据等间隔分成4 个子投影数据,以消除相邻探测器间的影响;接着分别对4 个子投影数据进行小波分解,然后分别对近似分量和垂直细节分量进行滤波处理,以消除具有高频特性的直线信息;随后对处理后的小波系数矩阵进行小波重构生成4 个新的子投影数据,继而合成为新的线积分投影数据;最后再用加权均值滤波方法对新的线积分投影数据进行滤波处理,处理后的线积分投影数据采用滤波反投影方法进行图像重建。实验结果表明,本文所提出的方法可有效地去除环形伪影。
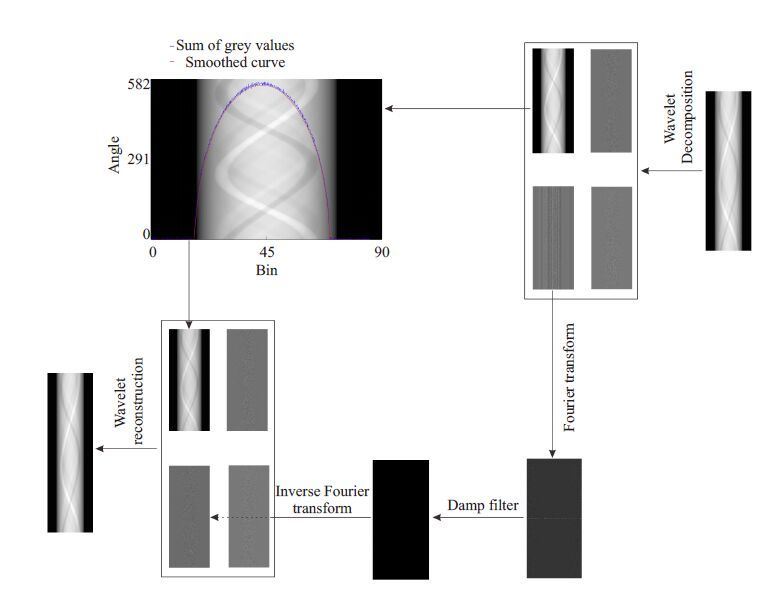
1 方法基于小波变换的CT 图像环形伪影去除方法主要包括3 个步骤:(1)获取子投影数据:将线积分投影数据等间隔分成四个子投影数据;(2)去除条形伪影:对每个子投影数据进行小波分解,生成小波系数矩阵,然后对小波系数中近似分量和垂直方向细节分量进行滤波处理,新的小波系数矩阵进行小波重构生成四个新的子投影数据(如图 1 所示);(3)去除残余条形伪影:采用加权均值滤波方法去除残余的条形伪影以获得最终线积分投影数据。具体步骤详述如下。
|
图 1 条形伪影去除算法流程图 Figure 1 Flowchart of the procedure to remove stripe artifacts. |
相邻探测器通道的数据相关性会影响条形伪影去除效果[1],本文将经对数变换后的线积分投影数据S等间隔分成L个子投影数据Si,以消除相邻探测器通道的数据相关性。子投影数据获取过程如下:
| $\begin{align} & {{S}_{i}}\left( n,{{j}_{m}} \right)=S\left( n,j \right):for1\le {{j}_{m}}\le {{j}_{d}}and \\ & \bmod \left( j,L \right)=\bmod \left( i,L \right) \\ \end{align}$ | (1) |
其中1 ≤ n ≤ ntotal,1 ≤ j ≤ jtotal,ntotal和jtotal分别表示投影个数和探测器通道个数,并且mod(i,L)表示i(1 ≤ i ≤ L)和L做除法运算后的余数。在本文中,L = 4。
1.2 条形伪影去除线积分投影数据经过小波分解后,条形伪影数据信息主要集中在近似分量和垂直方向细节分量中[6]。因此,步骤2.1 所获得的子投影数据Si(i = 1,2,3,4)分别进行一级小波分解,可以获得近似分量(如Ai,i = 1,2,3,4),水平方向细节分量(如Hi,i = 1,2,3,4),垂直方向细节分量(如Vi,i = 1,2,3,4)和对角线方向细节分量(如Di,i = 1,2,3,4)(如图 1所示)。对于垂直方向细节分量的系数,先进行傅里叶变换,然后采用带阻尼滤波器处理环形伪影数据[6, 12]。对于近似分量的系数,采用加权均值滤波去除环形伪影数据。计算步骤如下:
(1)沿投影角度方向求和:
| ${{a}_{i}}\left( m \right)=\sum\nolimits_{k}{{{A}_{i}}\left( k,m \right)}$ | (2) |
其中k,m表示近似分量维度大小。
(2)沿探测器单元方向加权均值滤波:
| ${{{\hat{A}}}_{i}}\left( k,m \right)={{A}_{i}}\left( k,m \right)\frac{{{{\hat{a}}}_{i}}\left( m \right)}{{{a}_{i}}\left( m \right)}$ | (3) |
| ${{{\hat{a}}}_{i}}\left( m \right)=\psi {{a}_{i}}\left( m \right)+\left( 1-\psi \right)\hat{a}{{'}_{i}}\left( m \right),0\le \psi \le 0.5$ | (4) |
| $\hat{a}{{'}_{i}}\left( m \right)=\frac{1}{2N+1}\sum\limits_{q=-N}^{N}{{{a}_{i}}\left( m+q \right)}$ | (5) |
其中
滤波后的小波系数矩阵进行小波重构生成新的子投影数据
如果2.2 中得到的线积分投影数据
为了验证本文方法的有效性,我们通过真实体模和小鼠实验分别进行了定性分析和定量分析。实验数据获取采用Siemens Inveon PET-CT 扫描设备采集,管电压为80 kVp,管电流为100 mAs。我们分别对含有环形伪影的真实体模CT 图像和小鼠CT 图像(图 2)进行环形伪影去除实验。由于本文算法与Munch 提出的方法在环形伪影的处理策略上相似,我们将对两者进行试验对比。实验平台为Windows 7,Intel(R)Core(TM)i5-2400 处理器,3.10 GHz,6 GB 内存,程序设计采用Matlab编程实现。

|
图 2 带有环形伪影的CT测试图像 Figure 2 Original images with artifacts reconstructed from the raw sinogram data. A: Resolution phantom; B: Rat chest. Both of the images are displayed in the same window: [0.030 0.055]. |
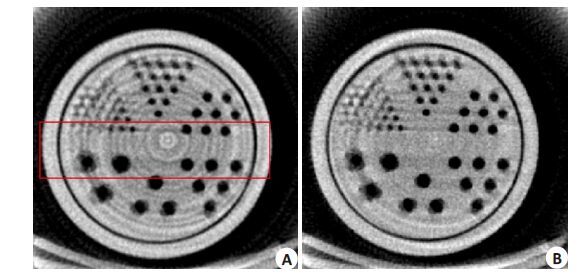
图 3A 是通过Munch 方法校正后的CT 图像,图 3B 是通过本文方法校正后的CT 图像。结合Munch 方法特点,易见,对于强度较大的环形伪影,Munch方法难以很好的去除。为了更清晰地比较两种方法对环形伪影去除效果,图 4 中给出图 3A 中所示的感兴趣区域对应的局部放大图。不难看出,本文方法能有效的进行环形伪影去除,且能保持图像细节。
|
图 3 体模CT图像环形伪影去除 Figure 3 Real phantom ring artifact removal study. A: Corrected image by Munch method; B: Corrected images by the proposed method. Both of the images are displayed in the same window: [0.030 0.055]. |

|
图 4 对应于图 3 的不同方法重建图像的感兴趣区域(ROI)的局部放大图 Figure 4 Zoomed ROI images of Fig. 3. A: Corrected image by Munch method; B: Corrected image by the proposed method. Both of the images are displayed in the same window: [0.030 0.055]. |
为了进一步定量分析本文方法,我们计算了图像的局部信噪比(LSNR),其中计算公式如下:
| $lSNR=\frac{\frac{1}{Q}\sum\limits_{m=1}^{Q}{\mu \left( m \right)}}{\sqrt{\frac{1}{Q}\sum\limits_{m=1}^{Q}{{{\left( \mu \left( m \right)-\frac{1}{Q}\sum\limits_{m=1}^{Q}{\mu \left( m \right)} \right)}^{2}}}}}$ | (6) |
其中μ表示校正后图像,Q表示感兴趣区域(ROI)内像素点个数。其中感兴趣区域如图 2A标记所示。由表 1 的分析可以看出,本文方法较Munch 方法提升了图像的局部信噪比。
| 表 1 不同方法感兴趣区域内的局部信噪比 Table 1 LSNRs of the ROI from different methods |
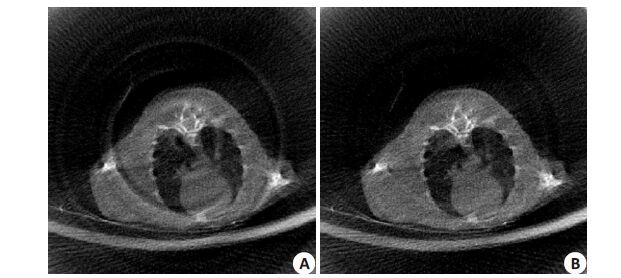
环形伪影去除结果如图 5~6 所示,其中图 5A 是小鼠CT原始投影数据,直线条结构信息明显。图 5B是通过Munch 方法校正后的CT 投影数据,强度较大的条形伪影依然存在。图 5C 是通过本文方法校正后的CT 投影数据,条形伪影可以基本上去除。图 6A 是通过Munch方法校正后的CT图像,图 6B是通过本文方法校正后的CT 图像。可以看到,我们的方法可以去除以图像中心为圆心的环形伪影,周围正常图像基本不受影响。而Munch 方法在靠近圆心的环形伪影能够被去除,但远离圆心的环形伪影无法消除。

|
图 5 小鼠CT投影数据条形伪影去除 Figure 5 Stripe artifact removal from rat chest sinogram data. A: Original sinogram; B: Corrected sinogram by Munch method; C: Corrected sinogram by the proposed method. Both of the images are displayed in the same window: [1.500 3.500]. |
|
图 6 小鼠CT图像环形伪影去除 Figure 6 Ring artifact removal from rat chest data. A: Corrected image by Munch method; B: Corrected image by the proposed method. Both of the images are displayed in the same window: [0.030 0.055]. |
环形伪影严重影响CT 图像质量,给图像噪声处理及图像分割等后续处理带来很大困扰,进而严重影响临床医生对CT 图像的正确诊断。Münch 等[6]对线积分投影数据进行小波变换,利用低通滤波方法滤除垂直方向的高频分量,可以实现弱强度环形伪影的去除,但是对于强度较大的环形伪影,Munch 方法处理的效果比较差,主要是因为在小波变换后,强度较大的条形伪影会被当成组织结构信息,因此Munch 方法不能够消除这些伪影。本文讨论分析了Munch 等提出的环形伪影去除方法,提出了一种基于投影域小波变换的CT 图像环形伪影去除方法。新方法把线积分投影数据等间隔分成四个子投影数据,接着分别对四个子投影数据进行小波分解,然后分别对近似分量和垂直细节分量进行滤波处理,对新的小波系数矩阵进行小波重构生成四个新的子投影数据,并合成为新的线积分投影数据,最后再用加权均值滤波对新的线积分投影数据进行滤波处理,处理后的线积分投影数据采用滤波反投影方法进行图像重建。基于投影域小波滤波处理的CT图像环形伪影去除方法是一种基于线积分投影数据的去除方法,此方法优于基于CT 重建图像的去除方法[2, 8-11],主要原因是经过小波滤波处理后的投影数据通过滤波反投影方法进行图像重建时,由于投影数据中几乎不含有条形伪影数据,使得重建后的CT图像的基本上去除了环形伪影,而且能很好地图像分辨率。试验结果表明,Munch方法虽然去除了部分环形伪影,但不能去除强度较大的环形伪影,而本文提出的方法相比Munch 方法不仅能很好地去除环形伪影,还提高了局部信噪比,较好的保持图像细节信息,使图像质量提高,有利于后续处理和量化分析。
| [1] | Tang X, Ning R, Yu R, et al. Cone beam volume CT image artifacts caused by defective cells in x-ray flat panel imagers and the artifact removal using a wavelet-analysis-based algorithm[J]. Med Phys,2001, 28 (5) : 812-25. DOI: 10.1118/1.1368878. |
| [2] | Sijbers J, Postnov A. Reduction of ring artefacts in high resolution micro-CT reconstructions[J]. Phys Med Biol,2004, 49 (14) : N247-53. DOI: 10.1088/0031-9155/49/14/N06. |
| [3] | Ashrafuzzaman A, Lee SY, Hasan MK. A Self-Adaptive approach for the detection and correction of stripes in the sinogram: suppression of ring artifacts in CT imaging[J]. EURASIP J Adv Signal Process,2011 (1) : 183547. |
| [4] | Boin M, Haibel A. Compensation of ring artefacts in synchrotron tomographic images[J]. Opt Express,2006, 14 (25) : 12071-5. DOI: 10.1364/OE.14.012071. |
| [5] | 余晓锷, 罗君芳, 陈武凡. 基于弦图的CT图像环形伪影校正[J]. 第四军医大学学报,2009 (3) : 207-9. |
| [6] | Münch B, Trtik P, Marone F, et al. Stripe and ring artifact removal with combined wavelet--Fourier filtering[J]. Opt Express,2009, 17 (10) : 8567-91. DOI: 10.1364/OE.17.008567. |
| [7] | Abu Anas EM, Lee SY, Hasan MK. Removal of ring artifacts in CT imaging through detection and correction of stripes in the sinogram[J]. Phys Med Biol,2010, 55 (22) : 6911-30. DOI: 10.1088/0031-9155/55/22/020. |
| [8] | Titarenko S, Titarenko V, Kyrieleis AA. A ring artifact suppression algorithm based on a priori information[J]. Appl Phys Lett,2009, 95 (7) : 71113. DOI: 10.1063/1.3211956. |
| [9] | Anas EM, Kim JG, Lee SY, et al. Comparison of ring artifact removal methods using flat panel detector based CT images[J]. Biomed Eng Online,2011, 10 (8) : 72. |
| [10] | Yang J, Zhen X, Zhou L, et al. Geometric correction for Cone- Beam CT Reconstruction and artifacts reduction [C]//Instru- mentation and Measurement Technology Conference, 2009: 14. |
| [11] | Chen YW, Duan GF. Independent component analysis based ring artifact reduction in cone-beam ct images[C]//2009 16TH Ieee international conference on image processing, VOLS 1-6, 2009: 4189-92. |
| [12] | Raven C. Numerical removal of ring artifacts in microtomography[J]. Rev of Sci Instru,1998, 69 (8) : 2978-80. DOI: 10.1063/1.1149043. |
 2015, Vol. 35
2015, Vol. 35
