2. 南方医科大学 基础医学院电子显微镜室,广东 广州 510515
2. Electron Microscope Lab, School of Basic Medical Sciences, Southern Medical University, Guangzhou 510515, China
透射电子显微镜(TEM)检查是肾活检病理检查的重要组成部分,肾组织内伴特殊有形结构的各种肾脏疾病的诊断及其新疾病的发现,大多通过电镜检查得以确诊[1]。北京大学肾脏病研究所对777例肾活检标本的病理诊断结果表明,电镜对18.5%的病例起决定性诊断作用,对13.5%的病例诊断提供重要参考作用[2]。但是用于透射电镜检测的样品要求标本块很小,通常超薄切片中只含有1~2 个肾小球,本身对于反映病变程度已有一定的局限性,再者目前透射电镜普遍配备的高分辨率CCD 数字化相机的视野都比较小,一张图片只能包含病变的局部,缺乏反映广泛病变区的信息,容易造成漏诊。如果要包含完整的病变区,如一个完整的肾小球,就只能在较低的放大倍率下进行图像采集,丧失了电子显微镜高分辨率的优势,拍摄的图像分辨率难以满足临床诊断的需要。这就产生了一个矛盾:既要保证图像清晰又要包含完整的病变区。目前肾活检所采集的TEM 图像很难达到两全,大大限制了TEM 在临床超微病理活检中的应用[3]。解决此问题最直接的方法就是将多张高分辨率且有一定重叠区域的TEM图像进行配准后拼接出一幅高分辨率、大视野的图像,为临床医生提供完整病变区域的高分辨率图像以提高病变诊断效率。
图像配准的方法主要分为基于像素的配准和基于特征的配准。基于像素配准的方法是利用两幅图像重叠区域的灰度信息构建相似性度量函数,求解匹配参数,从而建立图像的配准。常用的基于像素的配准方法有:基于相关性、互信息以及频域傅里叶方法等[4]。该类配准方法能充分利用图像信息,但对重叠区域小的图像很难估计准确的匹配参数[5]。基于特征的配准方法涉及到点特征、线特征和区域特征[4],点特征是最基本的特征,其适应范围最广且对其计算及描述都相对简单[6],因此,本文选择特征点的配准。基于特征点的方法通过提取具有几何不变性的点,由特征点之间的匹配得出匹配参数,从而建立图像的配准。几何不变性的特征点及其描述子的获取是该类方法的关键。Smith 等[7]用SUSAN 算子提取角点,但对角点的定位不够准确。Harris 等[8]提取出了具有高重复性检测率的harris 角点。Schmid 等[9]在此基础上,加入方向不变性的描述子,使该角点具有方向不变性的特点,但并不具备尺度不变性。Lowe等[10]在高斯差分空间提取出了对图像的尺度、方向具有不变性且有一定仿射不变性的sift 特征点。Yan等[11]对sift特征点的描述子用PCA方法进行降维得到pca-sift 特征点,虽然减少了计算量,但与sift 特征点相比,在尺度变化大以及图像较模糊时,匹配效果较差。Mikolajczyk 等[12]将sift 特征点中描述子转换为对数极坐标中计算,得出gloh特征点,虽然与sift特征点相比,gloh 特征点在光照变化大及图像较模糊时,匹配更有优势,但计算量更大[13]。Bay 等[14]利用hessian 矩阵来提取surf 特征点,提高了运算速度且在图像较模糊时优于sift特征点,但所估计的匹配参数不够稳定。Juan[15]、 Kayning 等[16]将这三种特征点进行比较,指出sift 特征点在尺度、旋转不变性以及匹配纹理复杂图像中均优于以上三种特征点,在仿射不变性中sift 与surf、gloh 相当。
由于sift 特征点具有较好的尺度和旋转不变性,对复杂纹理图像的配准,所估计的参数也相对稳定,因此本文选择基于sift特征点的配准方法对纹理复杂的肾小球TEM图像进行配准。由于显微镜成像系统导致了图像的形变和亮度不均匀,故而本文分别进行了配准的预处理和后处理。本文第1 节介绍了sift 特征点的提取、 两幅TEM图像的拼接过程以及多幅图像的完整拼接过程,第2节是实验结果,第3节为本文讨论。
1 方法 1.1 sift特征点的提取[10]sift 特征点是指图像中具有尺度、方向不变性且有一定仿射不变性的点,提取方法如下:
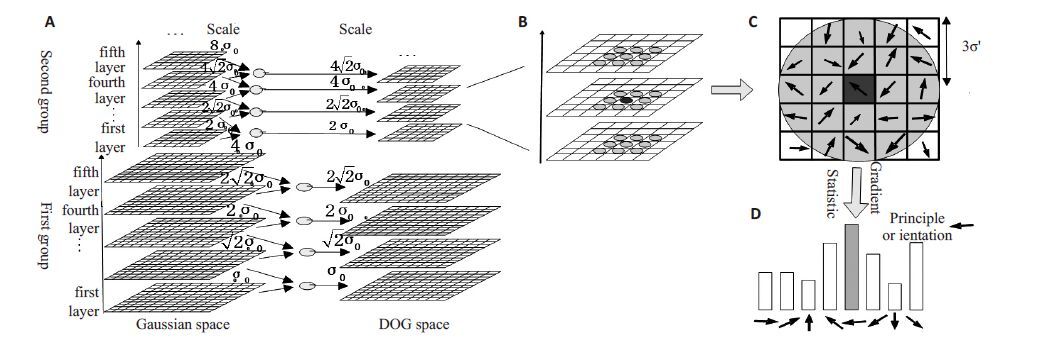
第1 步:构建图像高斯空间和高斯差分DOG(Difference of Gaussian)空间,如图 1A所示。
令I(x,y)为输入图像,由式(1)得到高斯空间第一组第一层图像L11(x,y,σ):
| $L_1^1\left( {x,y,{\sigma _1}} \right) = G{\left( {x,y,{\sigma _1}} \right)^*}I\left( {x,y} \right)$ | (1) |
G(x,y,σ0)表示尺度为σ0的高斯函数。*表示卷积。
然后由公式(2)构建高斯空间的第n组第i层图像Lni(x,y,σ0):
| $\begin{array}{l} L_n^i\left( {x,y,\sigma _n^i} \right) = G{\left( {x,y,{\sigma _1}} \right)^*}L_n^{i - 1}\left( {x,y,\sigma _n^{i - 1}} \right),\\ \left( {\sigma _n^i = k\sigma _n^{i - 1},\sigma = \sqrt {{{\left( {\sigma _n^i} \right)}^2} - {{\left( {\sigma _n^{i - 1},} \right)}^2}} ,i = 2,3,\cdots ,m,n = 1,\cdots ,l,} \right) \end{array}$ | (2) |
其中,l为高斯空间总组数,m为每组图像总层数,k = 21/m- 3为尺度系数。
再由公式(3)构建DOG 空间中第n组第i层图像Dni(x,y,σni):
| $\begin{array}{l} D_n^i\left( {x,y,\sigma _n^i} \right) = L_n^{i + 1}\left( {x,y,\sigma _n^i} \right) - L_n^i\left( {x,y,\sigma _n^{i - 1}} \right),\\ \left( {i = 1,2,\cdots ,m - 1} \right) \end{array}$ | (3) |
本文中取
第2步:提取特征点,并确定特征点方向。特征点在DOG空间中同组且相邻的三层图像中提取,如图 1B所示,若●所示像素点的灰度值是周围26像素点灰度值的极值,则将该像素点作为特征点。若σ′为特征点所在图像层的尺度,以特征点为中心,计算3σ′半径范围内像素点的梯度,如图 1C,再对该范围内梯度进行直方图统计,将统计出的主方向作为特征点的方向,如图 1D。
|
图 1 提取sift特征点[10] Figure 1 Extracting sift features. |
第3步:计算特征点的128维向量描述子。本文在特征点周围16 × 16邻域内计算描述子。先计算出该区域内梯度的方向和幅值,为保持方向不变性,将该区域内所有像素的方向以特征点的方向为基准进行调整。然后将该邻域分解为4 × 4个子区域。最后将各子区域中的梯度统计到8个方向中,获得128维向量描述子。
1.2 图像拼接图像拼接是利用多张有一定重叠范围的小视野的图像,获取一幅高分辨率、无缝的大视野图像的方法。本文图像拼接的方法由图像几何畸变校正、图像配准、 图像融合三部分组成,其中基于sift 特征点的图像配准是图像拼接的关键。
1.2.1 图像配准[10]本文基于sift 特征的图像配准方法包括以下3 步:第1 步:sift 特征点的匹配。令图像i、j为相邻的两张图像,根据1.1 节的方法分别提取图像i 、j 中sift 特征点集
| $x_k^{\left( j \right)} = {H_{ij}}x_k^{\left( i \right)} = \left[{\begin{array}{*{20}{c}} {{h_{11}}}&{{h_{12}}}&{{h_{13}}}\\ {{h_{21}}}&{{h_{22}}}&{{h_{23}}}\\ 0&0&1 \end{array}0} \right]x_k^{\left( i \right)}$ | (4) |
其中,Hij 是一个仿射变换矩阵,可根据RANSAC(Random Sample Consensus)算法计算出;第3步:将图像投影到同一平面中得到配准图像。以图像i所在的平面为参考平面,对于图像j中的任意一点(x,y),其在图像i中的投影(x′,y')由式(5)求得。
| ${\left( {x',y',1} \right)^{\rm{T}}} = H_{ij}^{ - 1}{\left( {x,y,1} \right)^{\rm{T}}}$ | (5) |
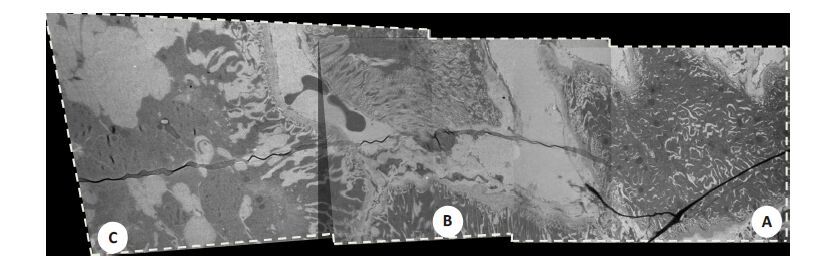
图 2是3张大小相同的图像配准结果。在配准时,从右往左先将两张图配准,再将配准结果与第3张图进行配准。从图中可以看出3张图像能正确配准,只是图像出现了不同程度的形变,图中虚线框表示3张原图的边界投影到同一平面上的结果,从图 2B的边界框可看出边界之间不再完全平行或垂直,并且从图 2C的边界框可看出,随着配准图像数目的增加,这种形变会变大。Kaynig等[16]说明了形变的原因在于聚光透镜系统对图像产生的几何畸变。因此,在图像配准之前,应先进行图像畸变校正预处理。
|
图 2 未经几何校正的图像配准 Figure 2 Image alignment before distortion correction(from A to C). |
Kaynig 等[16]针对TEM 图像畸变提出了用多项式来拟合非线性校正场的方法,并借助匹配的sift 特征点来估计多项式参数。对于任意点(x,y),其校正公式为:
| $\begin{array}{l} F = {\phi _d}\left( {x,y} \right)\beta = \left( {1,x,y,{x^2},xy,{y^2},\cdots ,{y^d}} \right)\\ {\left( {{\beta _1},{\beta _2},\cdots {\beta _{\frac{{\left( {d + 1} \right)\left( {d + 2} \right)}}{2}}}} \right)^T} \end{array}$ | (6) |
其中,d为拟合校正场的最高阶,本文中d = 5,β是由校正系数βi构成的向量。
对于所估计的校正场,当所有特征点经过校正后,通过旋转和平移转换到同一平面坐标时,匹配的特征点能近似对齐。若图像i经过仿射变换A(i)与图像j在同一平面对齐,令R(i)和T(i)为A(i)中提取出的旋转矩阵和平移矩阵,则满足:
| $\underset{\beta ,R,T}{\mathop{\min }}\,\sum\limits_{\begin{smallmatrix} i,j=1 \\ i\ne j \end{smallmatrix}}^{k}{\left( \begin{align} & {{\left\| \left( {{\phi }_{d}}\left( X_{n'}^{\left( i \right)} \right)\beta {{R}^{\left( i \right)}}+{{T}^{\left( i \right)}} \right)-\left( {{\phi }_{d}}\left( X_{n'}^{\left( j \right)} \right)\beta {{R}^{\left( j \right)}}+{{T}^{\left( j \right)}} \right) \right\|}^{2}} \\ & +\lambda {{\left\| \left( {{\phi }_{d}}\left( X_{n'}^{\left( i \right)} \right)\beta -X_{n'}^{\left( i \right)} \right) \right\|}^{2}} \\ \end{align} \right)}$ | (7) |
| $\underset{A}{\mathop{\min }}\,\sum\limits_{\begin{smallmatrix} i,j=1 \\ i\ne j \end{smallmatrix}}^{B}{{{\left\| X_{n'}^{\left( i \right)}{{A}^{\left( i \right)}}-X_{n'}^{\left( j \right)}{{A}^{\left( j \right)}} \right\|}^{2}}}$ | (8) |
其中,k为估计校正场所输入的图像数,本文中k = 9,λ = 0.01。
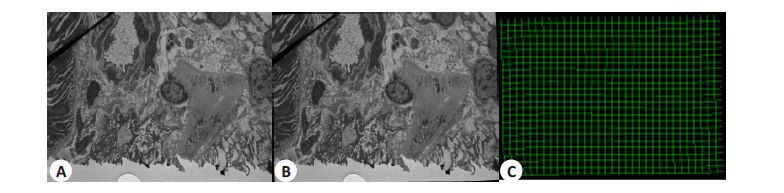
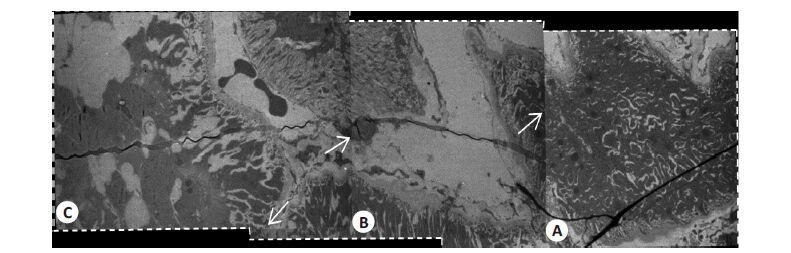
图像校正结果如图 3所示,A为校正前的图像,B为校正后的图像,C 为本文方法中提取的非线性校正场F。通过图 3C可以观察到,该校正方法仅使图像的局部信息发生微小的形变,在校正后仍能保持图像的结构、 形态等细节信息。图 4 为图像经畸变校正后再进行图像配准的结果,将该图中虚线所示的边界线与图 2 中的比较,可以看出图像经过畸变校正后,能有效减小图像形变。然而,图像进行校正及配准后,在图像重叠区域的边缘仍然存在明显的接缝,如图 4 中白色箭头所示,因而需进行后处理以消除接缝。
|
图 3 图像校正前后的结果及非线性校正场F Figure 3 Results before,after distortion correction and non-linear correction field F. A: Original image; B: Image after distortion correction; C: Non-linear correction field F. |
|
图 4 校正后图像配准的结果 Figure 4 Images alignment after distortion correction with white arrows indicating obvious seams. |
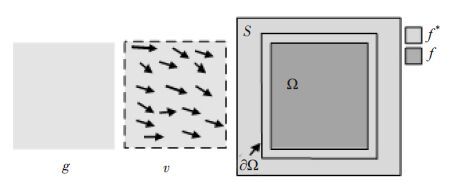
本文采用Poisson 图像编辑方法[17]将重叠区域的图像融合到配准的图像中以去除接缝。如图 5 所示,令g 为重叠区域图像,v 为g 的梯度场,s 为两张配准后的图像,Ω为g 融合于s 时对应的区域,∂Ω为Ω的边界。f 和f*分别为定义在Ω内和Ω外表示灰度的标量函数。
|
图 5 泊松编辑方法示意图 Figure 5 Schematic diagram of poisson image editing. f and f* are intensity functions inside and outside area respectively. |
为确保消除接缝的同时,重叠区域的梯度在融合前后近似相等,构造以下能量函数:
| $\underset{f}{\mathop{\min }}\,{{\iint_{\Omega }{{{\left| \nabla f-v \right|}^{2}},\left. s.t.f \right|}}_{\partial \Omega }}={{\left. {{f}^{*}} \right|}_{\partial \Omega }}$ | (9) |
该方程的解满足如下泊松方程:
| $\Delta f=divv,{{\left. f \right|}_{\partial \Omega }}={{\left. {{f}^{*}} \right|}_{\partial \Omega }}$ | (10) |
(10)式离散化的最优解满足:
| $\left| {{N}_{p}} \right|{{f}_{p}}-\sum\limits_{q\in {{N}_{p}}\cap \Omega }{{{f}_{q}}}=\sum\limits_{q\in {{N}_{p}}\cap \partial \Omega }{f_{q}^{*}}+\sum\limits_{q\in {{N}_{p}}}{{{v}_{pq}}}$ | (11) |
其中p为重建区域f中的任意点,Np为p点的四邻域,q为p 四邻域中任一点,vpq为
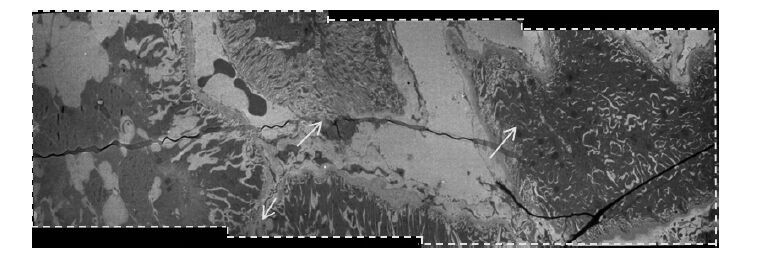
图 6 为泊松图像编辑方法消除图 4 中接缝的结果。从图中白色箭头所指处可以看出该方法能够很好地去除接缝。
|
图 6 泊松图像编辑方法消除接缝 Figure 6 Removing seams using Poisson image editing with white arrows indicatingoriginal seams removed. |
若输入n张有序的TEM图像,先提取相邻9张图像的sift特征点,进行特征点的匹配,根据匹配的特征点对图像进行几何畸变校正,并用所估计的校正场校正所有的图像。然后,对所校正的图像进行两张图像的配准,再进行配准后的无缝融合以得到两张图像的拼接。最后通过图像两两拼接的方式得到多幅图像的拼接。算法流程如下。

|
图 7 n张图像拼接流程图 Figure 7 Flow chart of multiple image stitching. |
本文实验数据来源于南方医科大学电子显微镜室采集的具有30%重叠区域的肾小球横切面图,该组数据为60 张5000 倍放大倍数的TEM 图像。实验选择了目前比较常用的图像处理软件中的拼接方法即fiji[18]中grid/collection stitching[19]功能、photoshop cs4[20]中photomerge功能以及ICE[21],与本文方法进行比较。
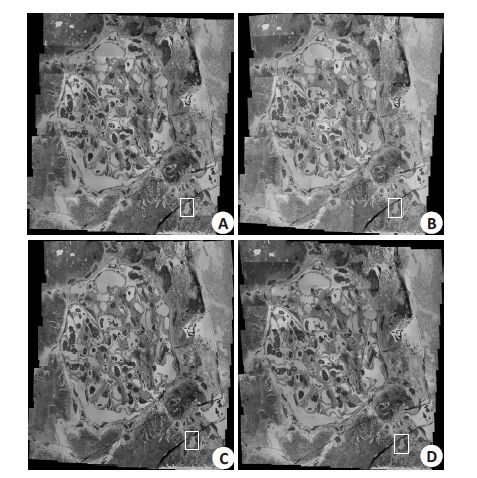
图 8为4种拼接方法对一个完整肾小球截面图的拼接结果,A~D 分别为fiji 软件中grid/collection stitching 功能、photoshop 中photomerge 功能、ICE 软件的拼接功能以及本文方法的结果。图像采集的范围是样本中包含肾小球的矩形区,由图 8 可以看出,各种拼接方法的结果均有一定程度的形变—锯齿样边缘,而比较四幅拼接图边缘与白色边框的距离可知:本文方法的形变最小,其主要原因是图像配准之前进行过图像校正。
|
图 8 四种不同拼接结果 Figure 8 Results of four different stitching methods,while white rectangular areas stitched juggling 3 adjacent imageand enlarged results show in Fig. 9 B~E. A: Stitching result of fiji; B: Stitching result of photoshop; C: Stitching result of ICE; D: Stitching result of proposed method. |
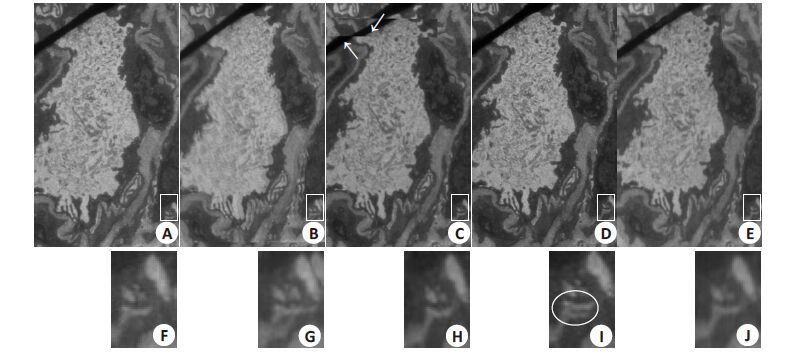
在图像的配准与缝融合的处理中,图像的部分重叠区域往往需要兼顾多张图像的配准与融合,因此处理好该局部是图像拼接的难点。图 9 中A 图截取于原采集图像,B~E 图为图 8 白色边框区域对应的放大图,该区域的拼接需要兼顾3 张图像,F~J 图为A~E 图白色边框区域对应的放大图。从图中可以看出:B 图整个区域都产生了伪影且在底部矩形框所示区域有明显的不对齐,C 图在箭头所指区域存在严重的不对齐,D 图中没有出现图像不对齐,但会造成图像细节信息的错误,如I图中椭圆标示处。
通过比较可以得出:本文采用的校正方法能够减小整幅图像拼接产生的形变,而且经校正后再配准能够得到比fiji、photoshop 更准确的配准结果,同时本文采用的图像融合的方法能够避免fiji方法中图像融合后产生的伪影以及ICE方法中图像细节信息的错误。
|
图 9 局部拼接结果 Figure 9 Stitching results of local area. A:Original image; B: Stitching result of fiji; C:Stitching result of photoshop; D: Stitching result of ICE; E:Stitching result of proposed method; F~J: Enlargedregions of rectangular areasin A~E. The white oval in image I indicatesartifact. |
本实验随机选取6 组相邻的图像,通过计算图像配准的误差作为对本文方法的评价。以误差函数即公式(12)作为量化评价的指标,误差值越小,说明配准方法越有效。
| ${{e}_{k}}={{\left\| x_{k}^{\left( j \right)}-{{H}_{ij}}x_{k}^{\left( i \right)} \right\|}^{2}}$ | (12) |
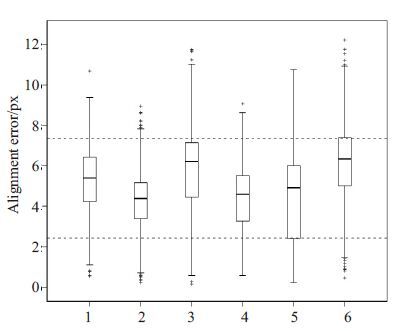
图 10 是由匹配的6 组图像中特征点的误差制成的箱图,每组中箱的上下两端各表示特征点误差的1/4 和3/4 的分位数,箱中的粗横线表示每组误差的平均值。“+”表示异常点。原图中像素的边长为25 nm,本文配准误差范围是62.5~187.5 nm。
|
图 10 6组图像中特征点的配准误差(px) Figure 10 Alignment errorsbetween matched features in six group of images. |
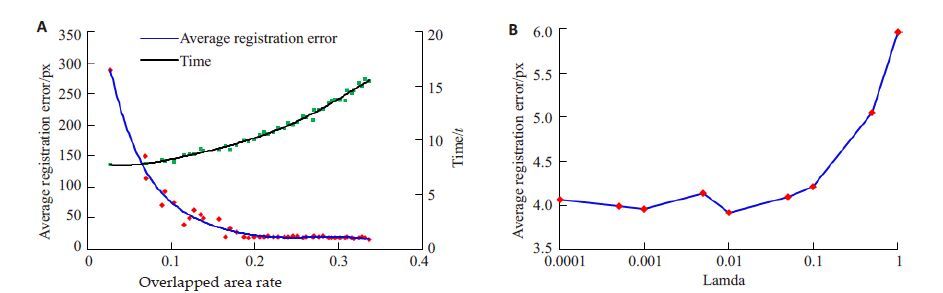
图像的重叠面积直接影响着特征点的个数以及计算的复杂程度。图 11A 反映了图像的重叠率对配准结果及运行时间的影响。实验结果表明图像面积的重叠率越大,图像平均配准误差越小但是配准时间越长,在重叠率超过0.2时,图像的平均配准误差变化不大,但是配准时间却显著上升。综合考虑配准误差以及时间,建议图像面积重叠率取0.2。
|
图 11 图像重叠面积对平均配准误差及时间的影响 Figure 11 Meters on average alignment error. A: Overlapped rate on average alignment error and time; B: Lamda on average alignment error. |
公式(7)中的正则化项是用来惩罚校正前后偏离太远的特征点对,在λ取适当值时,图像能在校正后保留图像细节信息,有助于图像正确配准。图 11B的实验结果表明,当λ小于0.01 时,平均配准误差在4px 附近波动,当λ大于0.01时,配准误差迅速上升。本文建议λ取0.01。
在多张图像的拼接中,通过图像的两两拼接会造成配准误差的累积,为减小整体配准误差可以先对所有配准参数进行整体优化后再进行图像配准。这将是本文今后的研究方向。
TEM图像能够在高分辨率下真实准确地反应组织和器官的内部信息,在临床病理活检标本的分析诊断中起着重要的作用。然而,TEM 图像难以兼顾高分辨率和大视野的需求,为此,本文提出了一种基于特征点的TEM 多幅图像拼接方法。该方法不仅能够避免图像产生伪影,增加图像配准的准确性,还能真实地保留图像信息。实验结果表明,本方法能够实现大视野高分辨率的TEM图像,获得高分辨率下的完整肾小球,为肾活检病理诊断提供有价值的信息,期待将来可以将此技术方法推广至透射电镜其它临床活检标本的超微病理诊断中。
| [1] | 王素霞, 柴立军, 谢燕玲, 等. 肾组织内特殊有形结构形成的肾脏病的电镜诊断[J]. 电子显微学报,2014, 33 (2) : 163-7. |
| [2] | 章友康, 王素霞. 超微病理在肾脏疾病诊断中的作用及其评价[J]. 诊断学理论与实践,2007, 6 (6) : 505-6. |
| [3] | 韩冬, 黄霞, 李波, 等. 透射电镜多图像拼接法测量纳米氧化镍的颗粒粒径[J]. 电子显微学报,2009, 28 (3) : 200-3. |
| [4] | 马俊, 曾玉龙, 范冲. 一种基于Keren 亚像素配准方法的改进算法[J]. 测绘与空间地理信息,2007, 30 (5) : 106-9. |
| [5] | Szeliski R. Image alignment and stitching: a tutorial[J]. Foundations and Trends in Computer Graphics and Vision,2006, 2 (1) : 1-104. DOI: 10.1561/0600000009. |
| [6] | 范大昭, 任玉川, 贾博, 等. 一种基于点特征的高精度图像配准方法[J]. 地理信息世界,2007, 5 (5) : 66-70. |
| [7] | Smith SM, Brady JM. SUSAN-a new approach to low level image processing[J]. Int J Comput Vision,1997, 23 (1) : 45-78. DOI: 10.1023/A:1007963824710. |
| [8] | Harris C, Stephens M. A combined corner and edge detector[C]// Proc of the Alvey Vision Conf, 1988: 147-51. |
| [9] | Schmid C, Mohr R. Local grayvalue invariants for image retrieval[J]. IEEE Trans Pattern Anal Mach Intell,1997, 19 (5) : 530-5. DOI: 10.1109/34.589215. |
| [10] | Lo we, David G. Distinctive image features from scale-invariant keypoints[J]. Int J Comput vision,2004, 60 (2) : 91-110. DOI: 10.1023/B:VISI.0000029664.99615.94. |
| [11] | Ke, Yan, and Rahul Sukthankar. PCA-SIFT: A more distinctive representation for local image descriptors[C]. Computer Vision and Pattern Recognition, 2004. CVPR 2004.// Proceedings of the 2004 IEEE Computer Society Conference on. Vol. 2.IEEE, 2004. |
| [12] | Mikolajczyk K, Schmid C. A performance evaluation of local descriptors[J]. Pattern Analysis and Machine Intelligence, IEEE Transactions on,2005, 27 (10) : 1615-30. DOI: 10.1109/TPAMI.2005.188. |
| [13] | T ao, Yuehua. Research progress of the scale invariant feature transform(SIFT)descriptors[J]. J Convergence InforTechnol,2010, 5 (1) : 116-21. DOI: 10.4156/jcit. |
| [14] | B ay, Herbert, TinneTuytelaars, Luc Van Gool. Surf: Speeded up robust features[J]. Computer Vision-ECCV 2006. Springer Berlin Heidelberg,2006, 110 (3) : 404-17. |
| [15] | Juan L, Oubong G. A comparison of sift, pca-sift and surf[J]. International Journal of Image Processing(IJIP),2009, 3 (4) : 143-52. |
| [16] | Kaynig V, Fischer B, Müller E, et al. Fully automatic stitching and distortion correction of transmission electron microscope images[J]. J StructBiol,2010, 171 (2) : 163-73. |
| [17] | Pérez PG, Andrew B. Poisson image editing[J]. ACM Transactions on Graphics(TOG),2003, 22 (3) : 313-8. DOI: 10.1145/882262. |
| [18] | Fiji. An image processing package based on imagej[Z], 2010. |
| [19] | Preibisch S, Saalfeld S, Tomancak P. Globally optimal stitching of tiled 3D microscopic image acquisitions[J]. Bioinformatics,2009, 25 (11) : 1463-5. DOI: 10.1093/bioinformatics/btp184. |
| [20] | Photoshop. An software for Image editing and compositing[Z], 2009. |
| [21] | ICE. An advanced panoramic image stitcher[Z], 2011. |
 2015, Vol. 35
2015, Vol. 35
