脑部磁共振图像是临床上对脑功能研究及脑组织疾病预测、诊断的主要手段。通过分割脑部磁共振图像中的海马,测量海马体积及形态研究[1-2],可对老年痴呆、颞叶癫痫、精神分裂等多种脑部疾病进行分析与诊断。然而,海马形状不规则,与周围灰质结构关系复杂,在磁共振图像中边缘模糊,边缘难以界定,对比度与信噪比均较低,使得传统的图像分割方法难以准确分割。目前常见的图像分割方法主要有:阈值分割、区域生长法、聚类算法、马尔科夫随机场及水平集的分割方法。阈值分割[3]实现简单、运行速度快,但阈值分割没有考虑空间信息,对噪声和不均匀性敏感。区域生长法[4]是一种鲁棒性强、速度快、无调节参数的分割算法。但它需要人机交互来选取种子像素,而且对噪声敏感。聚类算法[5]简单有效,是一种无监督的统计方法,但聚类算法没有考虑空间信息,对噪声敏感,而且聚类算法需要初始聚类数目、聚类中心,这对最终分割影响很大。基于马尔科夫随机场(Markov Random Field,MRF)分割方法[6]的关键是参数估计,如果没有足够的先验知识,就不能准确的估计参数,分割也就不准确。水平集方法[7]计算稳定、规划容易、可灵活的加入先验信息。但水平集分割方法对参数选择敏感,并且容易陷于局部极值。目前,海马的手动分割被视为所有分割方法的金标准,但手动分割耗时费力,重复性低,且非常依赖分割者的经验及解剖学知识。基于图谱配准的分割方法充分利用手动分割的形状先验知识,通过图谱与待分割图像配准,把图谱中存储的形状先验信息直接映射到待分割图像中,实现一种全自动的“专家”(图谱)指导下的图像分割。基于图谱配准的分割方法引入了形状先验信息,无需手动设置初始边界、对噪声和偏移场不敏感,因而获得了广泛的应用与认可。Baillard等[8]利用基于单图谱的分割方法分割出脑部结构,得到较好的分割结果。但考虑到人体解剖结构的差异,单图谱分割难以适应不同个体脑部结构的差异,容易产生错误分割,特别是边界处的分割。基于多图谱配准的分割方法[9]利用多组医学图谱来降低图谱选择的不确定性。基于多图谱配准的分割方法采用了多组图谱,因此需要融合算法将多组分割结果融合在一起,图 1是基于多图谱配准的分割过程。
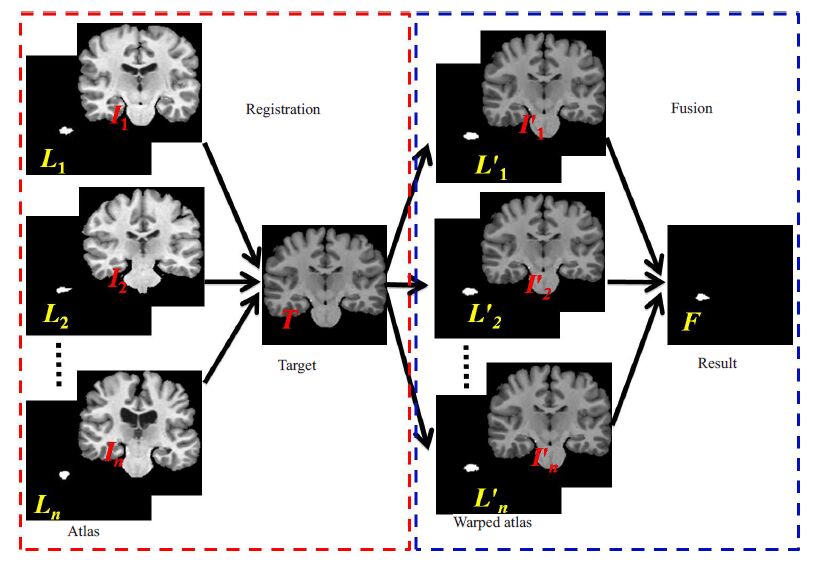
|
图 1 基于多图谱配准分割的图示说明 Figure 1 The description of the multi-atlas based segmentation. |
标号融合是基于多图谱配准分割的关键步骤,标号融合算法也是近几年基于多图谱配准分割的研究重点,常见的标号融合算法主要有Major Voting[10]、WeightVoting[11]、STAPLE[12]、Spatial STAPLE[13]、SIMPLE[14]。这些融合算法都只利用了图谱标号图像,没有考虑待分割图像的灰度与结构信息,因此得到的分割结果表面不光滑,在边界出现阶梯状。本文考虑待分割图像与图谱配准的局部相似性测度,将其作为权重计算海马的局部权重概率图谱,配准的相似性测度加权考虑配准的精度,提高概率图谱计算的准确性。并在计算概率图谱时,引入距离场的概念并用距离场对图谱标号图像进行加权,距离场加权考虑了图谱标号图像提供的位置信息。然后根据待分割图像中像素与其局部邻域内像素的相似性,称之为自相似性,利用它对包含位置信息的局部权重概率图谱进行优化,自相似性优化考虑待分割图像提供的灰度与结构信息,保证了信息的完整性,降低噪声的影响,同时考虑邻域像素的分割情况,提高分割精度。
1 材料与方法 1.1 实验数据为了验证本文方法的正确性与有效性,将本文方法与国际上主流的分割方法进行对比实验,包括MajorVoting,Weight Voting 和SIMPLE,STAPLE,SpatialSTAPLE 算法。实验数据采用在线图像数据库MICCAI 2013(http://www.miccai2013.org/index.html)公开的脑部数据,该数据集包含35组T1加权的脑部磁共振图像三维数据,每组数据包含图谱灰度图像及对应的专家手动勾画的标号图像。实验运行环境:Windows 7 Service Pack 1,Intel(R) Core(TM)i5-3330 CPU,4.0 G内存。
1.2 算法流程本文方法包括预处理、图像配准、配准的相似性测度加权、标号图像的距离场加权、待分割图像的自相似性加权、阈值处理六部分。本文方法的系统流程图如下图 2所示。
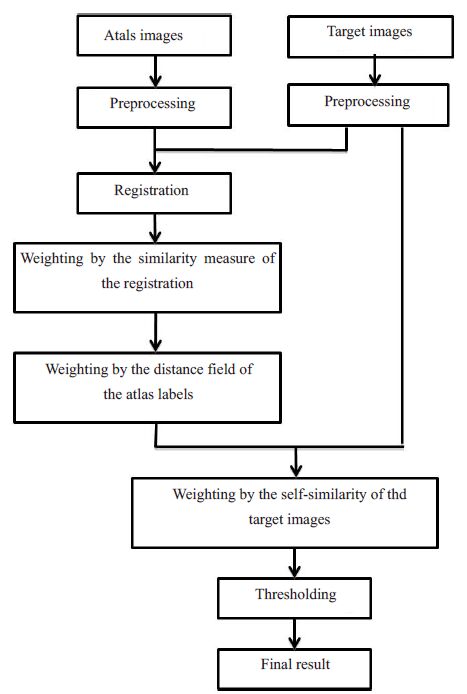
|
图 2 系统流程图 Figure 2 Flowchart of the proposed method. |
在前期工作中[15]我们发现:脑壳、偏移场、灰度归一化都会对配准和分割有一定的影响,我们利用BET算法去除脑壳[16];N4算法对MR图像中的偏移场[17]进行校正;并对图像进行灰度归一化从而完成图像的预处理,下图 3为预处理后的图像。
|
图 3 预处理后的脑部磁共振图像 Figure 3 Preprocessed brain MR image. |
为了利用手动分割精度高的优势,将图谱中存储的形状先验信息映射到待分割图像,采用DRAMMS算法[18]将图谱灰度图像Ii配准到待分割图像T,得到变形场和形变后的图谱灰度图像Ii’,然后利用变形场对相应的图谱标号图像进行变形Li,得到形变后的图谱标号图像Li’。
1.2.3 配准的相似性测度加权概率图谱理论[19]的基本思想是选取一组图谱,通过图谱与待分割图像配准,得到形变后的标号图像,再通过一定的算法,由形变后的标号图像计算出每个像素属于目标的概率值,即目标的概率图谱。传统的概率图谱算法为平均概率图谱,其计算公式为:
| $P\left( x,y,z \right)=\frac{1}{n}\sum\limits_{i=1}^{n}{{{{{L}'}}_{i}}\left( x,y,z \right)}$ | (1) |
式中n为图谱个数,Li’为像素(x,y,z)的标号,在实验中,为了方便计算,标号取+1及-1,分别表示是否为目标。平均概率图谱的计算精度依赖于配准的精度,在图谱与待分割图像配准精度不高时,容易产生误差。本文考虑待分割图像中像素点与形变后图谱中像素点的局部相似性即配准的相似性测度,将其作为权重来计算概率图谱,本文称之为局部权重概率图谱,局部权重概率图谱计算公式为:
| ${{P}_{w}}\left( x,y,z \right)=\frac{\sum\limits_{i=1}^{n}{{{w}_{i}}\left( x,y,z \right)\times {{{{L}'}}_{i}}\left( x,y,z \right)}}{\sum\limits_{i=1}^{n}{{{w}_{i}}\left( x,y,z \right)}}$ | (2) |
其中wi为形变后图谱图像Ii’与待分割图像T配准的局部相似性测度。传统方法如互信息量、互相关系数、归一化的互相关或者其它的相似性测度在计算变形后的图谱与待分割图像的相似性时,额外增加了计算量,比较耗时,而且这种整体的相似性测度并不能很好的度量每个像素点在配准、分割时的作用。我们使用NCC(normalized correlation coefficient)[11]计算配准的局部相似性测度,并将其作为权重,相似性测度越高的像素点,说明配准更加准确,对最后的分割结果影响就越大。
1.2.4 标号图像的距离场加权局部权重概率图谱利用配准的相似性测度对图谱标号图像进行加权,但局部权重概率图谱仅仅只利用了标号图像提供的标号信息,没有利用其暗含的位置信息。我们将图谱标号图像Li’进行距离变换,得到包含位置信息的距离场di,然后用距离场di对标号图像进行加权,得到包含位置信息的标号图像DL,称之为距离标号图像。则包含距离信息的概率图谱计算公式为:
| ${{P}_{dw}}\left( x,y,z \right)=\frac{\sum\limits_{i=1}^{n}{{{w}_{i}}\left( x,y,z \right)\times D{{L}_{i}}\left( x,y,z \right)}}{\sum\limits_{i=1}^{n}{{{w}_{i}}\left( x,y,z \right)}}$ | (3) |
| $D{{L}_{i}}\left( x,y,z \right)={{d}_{i}}\left( x,y,z \right)\times {{{{L}'}}_{i}}\left( x,y,z \right)$ | (4) |
利用距离标号图像DLi替换掉原来的标号图像Li’的理论依据是:图谱标号图像中,标号为+1的像素点,到边界的距离越大,刚它周围的像素属于目标的可能性也越大;反之,标号为-1 的像素,如果它到边界的距离越大,则它周围的像素不属于目标的可能性也越大。
1.2.5 待分割图像的自相似性加权自相似性衡量像素与其邻域内像素基于邻域的相似程度。本文考虑待分割图像中像素与其局部邻域内像素的自相似性,利用它对包含距离信息的局部权重概率图谱进行优化。自相似性优化的原理:区域内相邻像素的相似度越高,它们属于同一目标的概率就越大,即标号相同的可能性越大。图 4为自相似性的图示说明。
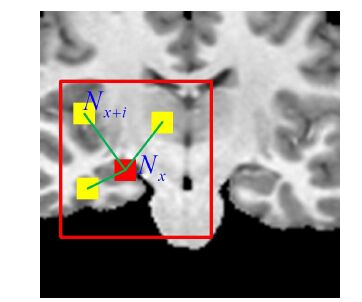
|
图 4 自相似性的图示说明 Figure 4 The description of self-similarity. x is the centerpixel of the red image patch Nx,x+i is neighbour pixel ofpixel x,and it is the center pixel of the yellow image patchNx+i.。The red box is search area of pixel x. |
自相似性的计算公式:
| ${{S}_{i}}\left( x \right)=\exp \left( -\frac{{{D}_{P}}\left( {{N}_{x}},{{N}_{x+1}} \right)}{V\left( {{N}_{x}},i \right)} \right),i\in R$ | (5) |
| ${{D}_{P}}\left( {{N}_{{{x}_{1}}}},{{N}_{{{x}_{2}}}} \right)={{\sum\limits_{j\in P}{\left( A\left( {{x}_{1}}+j \right)-A\left( {{x}_{2}}+j \right) \right)}}^{2}}$ | (6) |
式中Si为自相似性,衡量像素x
| ${{P}_{sdw}}\left( x,y,z \right)=\frac{\sum\limits_{i=1}^{R}{{{S}_{i}}\left( x,y,z \right)\times P_{sdw}^{i}\left( x,y,z \right)}}{\sum\limits_{i=1}^{R}{{{S}_{i}}\left( x,y,z \right)}}$ | (7) |
由公式(7)得到自相似性优化的局部权重概率图谱,对其进行阈值处理,即可得到最终的分割结果F。
| $F\left( x,y,z \right)=\left\{ \begin{array}{*{35}{l}} 1,{{P}_{sdw}}\left( x,y,z \right)>0 \\ 0,{{P}_{sdw}}\left( x,y,z \right)<0 \\ \end{array} \right.$ | (8) |
为验证本方法的有效性,我们与目前国际上主流的几种方法进行了比较,分别为Major Voting,WeightVoting 和SIMPLE,STAPLE,Spatial STAPLE。采用Dice 相似度(Dice Similarity Coefficient,DSC)作为评价分割结果的标准,其定义式为:
| $DSC\left( A,B \right)=\frac{2V\left( A\bigcap B \right)}{V\left( A \right)+V\left( B \right)}$ | (9) |
其中V(A)、V(B)分别表示自动分割结果和专家手动勾画结果的体积,V(A ⋂B)表示自动分割结果和专家手动勾画结果重叠部分的体积。
图 5给出了不同分割方法对左、右海马分割结果与手动分割结果的重叠率箱线图。观察比较箱线图,Major Voting、Weight Voting、SIMPLE、STAPLE 和Spatial STAPLE 五种方法对左海马分割,五种方法中仅Spatial STAPLE的Dice 相似度为85.8%左右,而本文方法可达到87%,提高了1.2%;对右海马传统方法分割的Dice相似度为86.5%左右,而本文方法为87.5%左右,提高了1%。而且本文方法的箱线图比较短,说明本文方法具有较好的一致性。
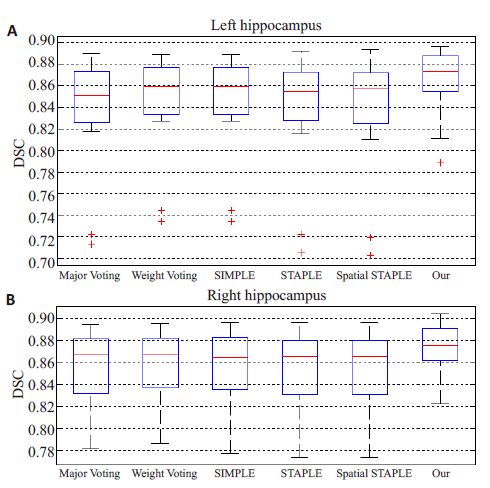
|
图 5 不同分割方法对左、右海马分割结果与手动分割结果重叠率箱线图 Figure 5 Box-plot of performance metric for segmentation methods,ascompared against manual segmeatation. A is the left hippocampusresult and B is the right hippocampus result |
图 6A-F 给出了Major Voting、Weight Voting、SIMPLE、STAPLE和Spatial STAPLE 及本文方法对编号为1002数据中的左海马分割的截面图。图中的绿色轮廓为专家手动分割的结果,红色轮廓为不同方法的分割结果。从图 6F中可以看出本文方法与专家手动分割的结果更加接近,而且本文方法的结果更加光滑,这是因为自相似性加权考虑待分割图像的灰度与结构信息对分割结果进行了优化,从而得到光滑、准确的分割结果。
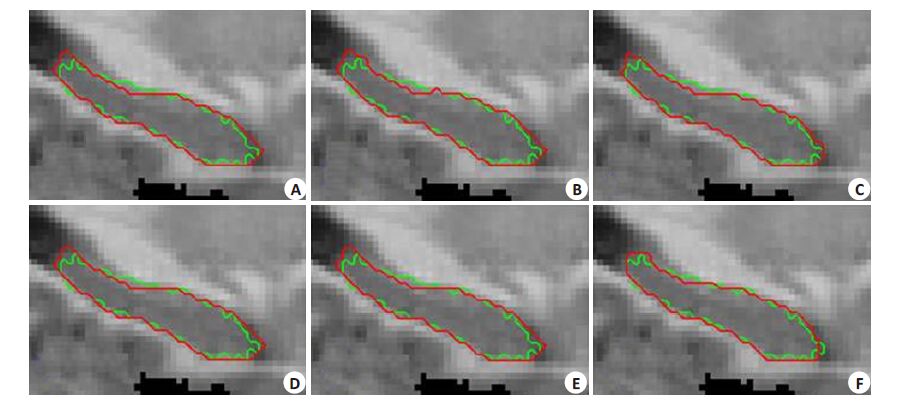
|
图 6 不同方法分割左海马的截面图 Figure 6 Sagital view of the various segmetation results. A-F:Major Voting,Weight Voting,SIMPL,STAPLE,Spatial STAPLEand the proposed method. The manually segmentation result are illustrated in green contour,the automatic segmentationresults are illustrated in red contour. |
表 1给出了不同分割方法对编号为1002号数据中左、右海马分割时的标号融合时间。Major Voting、Weight Voting、SIMPLE、STAPLE 和Spatial STAPLE及本文方法都为标号融合算法,使用以上方法对海马进行分割时,图像预处理及图谱与待分割图像配准花费的时间是相同的,总分割时间的差别是在标号融合这一步,所以只比较标号融合花费的时间。由表 1 可以看出,本文方法与传统方法相比,花费时间略有增加,这主要是利用自相似性进行加权花费的时间,而且MajorVoting、Weight Voting、SIMPLE、STAPLE 和SpatialSTAPLE的程序都是经过优化好的工具包,而本文程序采用Matlab进行编程实验,再次本文的标号融合时间与传统方法相比是可以接受的。
| 表 1 不同方法标号融合时间 Table 1 Fusion time for various label fusion methods(s) |
为了进行对照实验,验证每种加权的有效性,分别对平均概率图谱、局部权重概率图谱、包含位置信息的局部权重概率图谱及自相似性加权的局部权重概率图谱进行阈值处理得到分割结果。为了方便画图,我们分别称平均概率图谱、局部权重概率图谱、包含位置信息的局部权重概率图谱及自相似性加权的局部权重概率图谱得到的分割结果为Mean、W、WW、及WWW。图 7给出了左、右海马的分割结果。观察比较箱线图中的红线可以看出,配准的相似性加权、距离场加权及自相似性加权都能明显的提高分割精度。
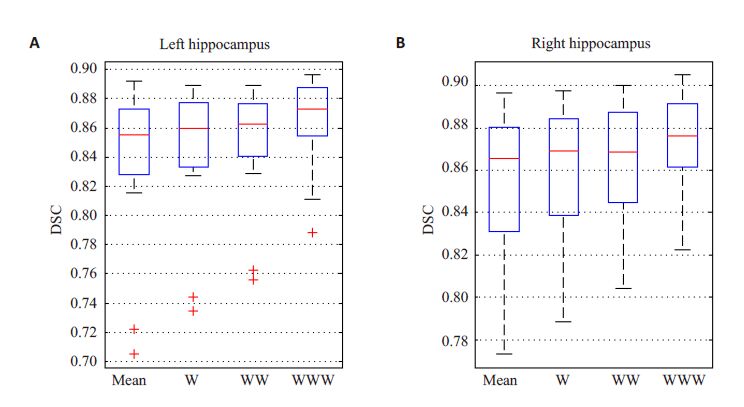
|
图 7 不同分割方法对左、右海马分割结果与手动分割结果重叠率箱线图 Figure 7 Box-plot of performance metric for segmentation methods, as compared against manual segmeatation. A is the left hippocampus result and the B is the right hippocampus result. |
大脑内部结构的位置、体积与形态变化与多种疾病息息相关,而要确定和分析这些变化首先需要对这些脑结构进行精确的分割。我们对目前脑内结构分割方法进行了详细分析,并针对这些方法存在的缺点和不足,提出了一种新的基于多权重概率图谱的脑部图像分割方法。新方法中包含三种加权:配准的相似性测度加权、标号图像的距离场加权和待分割图像的自相似性加权。通过三种加权来保证概率图谱计算的准确性,而概率图谱的准确性将直接影响到分割的精度,实验结果表明,本文分割方法可准确、鲁棒性地分割海马。
| [1] | Morra JH, Tu Z, Apostolova LG, et al. Validation of a fully automated 3D hippocampal segmentation method using subjects with Alzheimer's disease mild cognitive impairment, and elderly controls[J]. Neuroimage,2008, 43 (1) : 59-68. DOI: 10.1016/j.neuroimage.2008.07.003. |
| [2] | Yushkevich PA, Wang H, Pluta J, et al. Nearly automatic segmentation of hippocampal subfields in in vivo focal T2-weighted MRI[J]. Neuroimage,2010, 53 (4) : 1208-24. DOI: 10.1016/j.neuroimage.2010.06.040. |
| [3] | Manikandan S, Ramar K, Willjuice Iruthayarajan M, et al. Multilevel thresholding for segmentation of medical brain images using real coded genetic algorithm[J]. Measurement,2014, 47 (0) : 558-68. |
| [4] | Lu XQ, Wu JS, Ren XY, et al. The study and application of the improved region growing algorithm for liver segmentation[J]. Optik-Internation Journal for Light and Electron Optics,2014, 125 (9) : 2142-7. DOI: 10.1016/j.ijleo.2013.10.049. |
| [5] | Yao H, Duan QL, Li DL, et al. An improved K-means clustering algorithm for fish image segmentation[J]. Mathematical and Computer Modelling,2013, 58 (3-4) : 790-8. DOI: 10.1016/j.mcm.2012.12.025. |
| [6] | Park SH, Lee S, Yun ID, et al. Hierarchical MRF of globally consistent localized classifiers for 3D medical image segmentation[J]. Pattern Recognition,2013, 46 (9) : 2408-19. DOI: 10.1016/j.patcog.2013.02.014. |
| [7] | Li CM, Huang R, Ding ZH, et al. A level set method for image segmentation in the presence of intensity inhomogeneities with application to MRI[J]. IEEE Trans Image Process,2011, 20 (7) : 2007-16. DOI: 10.1109/TIP.2011.2146190. |
| [8] | Baillard C, Hellier P, Barillot C. Segmentation of brain 3D Mr images using level sets and dense registration[J]. Med Image Anal,2001, 5 (3) : 185-94. DOI: 10.1016/S1361-8415(01)00039-1. |
| [9] | Jia HJ, Yap PT, Shen DG. Iterative multi-atlas-based multi-image segmentation with tree-based registration[J]. Neuroimage,2012, 59 (1, SI) : 422-30. DOI: 10.1016/j.neuroimage.2011.07.036. |
| [10] | Aljabar P, Heckemann RA, Hammers A, et al. Multi-atlas based segmentation of brain images: Atlas selection and its effect on accuracy[J]. Neuroimage,2009, 46 (3) : 726-38. DOI: 10.1016/j.neuroimage.2009.02.018. |
| [11] | Sjöberg C, Ahnesjö A. Multi-atlas based segmentation using probabilistic label fusion with adaptive weighting of image similarity measures[J]. Comput Methods Programs Biomed,2013, 110 (3) : 308-19. DOI: 10.1016/j.cmpb.2012.12.006. |
| [12] | Warfield SK, Zou KH, Wells WM. Simultaneous truth and performance level estimation (STAPLE): An algorithm for the validation of image segmentation[J]. IEEE Trans Med Imaging,2004, 23 (7) : 903-21. DOI: 10.1109/TMI.2004.828354. |
| [13] | Commowick O, Akhondi-Asl A, Warfield SK. Estimating a reference standard segmentation with spatially varying performance parameters: local MAP STAPLE[J]. IEEE Trans Med Imaging,2012, 31 (8) : 1593-606. DOI: 10.1109/TMI.2012.2197406. |
| [14] | Langerak TR, Van Der Heide UA, Kotte AN, et al. Label fusion in atlas-based segmentation using a selective and iterative method for performance level estimation (SIMPLE)[J]. IEEE Trans Med Imaging,2010, 29 (12) : 2000-8. DOI: 10.1109/TMI.2010.2057442. |
| [15] | 胡昊, 张明慧, 卢振泰, 等. 基于多图谱配准的海马自动分割[J]. 计算机工程与设计,2014, 35 (3) : 975-80. |
| [16] | Popescu V, Battaglini M, Hoogstrate WS, et al. Optimizing parameter choice for FSL-Brain Extraction Tool (BET) on 3D T1 images in multiple sclerosis[J]. Neuroimage,2012, 61 (4) : 1484-94. DOI: 10.1016/j.neuroimage.2012.03.074. |
| [17] | Tustison NJ, Avants BB, Cook PA, et al. N4ITK: improved N3 bias correction[J]. IEEE Trans Med Imaging,2010, 29 (6) : 1310-20. DOI: 10.1109/TMI.2010.2046908. |
| [18] | Ou YM, Aristeidis S, Nikos P, et al. DRAMMS: Deformable registration via attribute matching and mutual-saliency weighting[J]. Medical Image Analysis,2011, 15 (14) : 622-39. |
| [19] | Mazziotta JC, Toga AW, Evans A, et al. A probabilistic Atlas of the human brain: theory and rationale for its development[J]. Neuroimage,1995, 2 (2) : 89-101. DOI: 10.1006/nimg.1995.1012. |
 2015, Vol. 35
2015, Vol. 35
