2. 南方医科大学生物医学工程学院 广东省医学图像处理重点实验室, 广东 广州 510515 ;
3. 南方医科大学生物医学工程学院 华南理工大学电子与信息学院, 广东 广州 510640
2. Guangdong Provincial Key Laboratory of Medical Image Processing, School of Biomedical Engineering, Southern Medical University, Guangzhou 510515, China ;
3. Institute of Medical Information, School of Electronic and Information Engineering, South China University of Technology, Guangzhou 510640, China
运动康复训练有助于恢复运动功能障碍患者的中枢神经系统功能,并可防止肌肉萎缩[1],以减轻运动功能障碍给患者及其家庭、社会带来的沉重负担。运动康复训练时,不仅要对患者施加精确的运动控制、记录治疗数据,更需要及时了解肌肉功能的改善情况,以改进训练方法和强度。肌肉结构特征参数,如肌肉厚度、肌纤维长度、羽状角等,常用于评估肌肉功能的变化[2-4]。
超声影像(US)技术具有无创、实时和便捷的优点,已经被越来越多地用于肌肉的研究。然而,临床医生往往是通过图像处理软件依靠手工标注的方法来确定这些肌肉结构参数[5],这限制了超声影像技术在骨骼肌肉临床研究中的应用。近几年,研究学者尝试通过各种算法对肌肉超声图像进行处理分析,以期自动获得这些参数[6-11]。Zhou 与Zheng[6]提出迭代霍夫变换(RevotingHough Transform)计算超声图像中肌纤维的羽状角,取得了良好的效果,并进一步应用该算法在肌肉运动过程中动态获取羽状角[8]。Zhao 和Zhang[11]采用雷登变换(Radon Transform)实现肌肉羽状角的自动跟踪和计算。这些方法基于超声灰度图像,斑点噪声对跟踪结果影响较大,需要对超声图像进行一些专门的预处理[6],例如降采样、插值、希尔伯特变换、幅度-亮度转换、去噪滤波等[10],以获得较好结果。而经预处理的超声灰度图像往往会丢失一部分超声射频原始信号所包含的有用信息,例如相位信息。
超声射频信号是原始信号,是入射超声波经生物组织反射、散射后形成的回波,富含组织内部信息。与基于灰度图的跟踪方法相比,基于射频信号的跟踪方法可利用更多的有用信息,且受斑点噪声影响较小。Luo和Konofagou[12]提出一种基于超声射频信号的快速归一化互相关方法进行心肌组织的位移估计,取得了较好的结果。
肌肉痉挛等腿部疾病都与腓肠肌有着直接或者间接的关系。当肌肉拉伸或收缩时,羽状角会随之变化[13]。羽状角的变化可反映肌肉的功能与状态,为临床上腓肠肌病变诊断以及运动康复训练提供重要的参考信息。本文提出腓肠肌羽状角的一种基于超声射频信号的自动测量方法,通过选定肌束的超声射频信号,利用互相关算法,分析射频信号的幅值和相位信息,自动跟踪肌束方向和肌腱膜方向,计算肌肉的羽状角。本方法分别用于人体和仿真体膜的超声数据,所检测的羽状角数值分别与手工测量结果和理论数值相比较,检验该算法的有效性。
1 材料和方法 1.1 人体超声数据的获取采用开放式综合超声系统(Sonix RP,Ultrasonix,Canada),该系统配有主机箱(包函PIV 3.0 GHz的双CPU、80 GB的系统硬盘、及1GB的存储器)、显示器、一张内置10 位模/数转换卡(采样频率40 MHz),以及一个中心频率10 MHz 的线阵超声探头(-6dB 带宽5~14 MHz)。该系统采用开放式PC 平台-Microsoft®Visual Studio®环境,可以同时保存超声图像、超声视频和超声射频信号。
受试者为正常男性,22~26 岁,坐姿,膝关节成近90°,脚着地,以脚跟为定点,踝关节背屈40°,保持不动。腓肠肌内侧头为研究对象,将超声探头沿腓肠肌纵向放置。当显示器清晰地显示出腓肠肌的羽状肌束结构时,采集超声射频信号(图 1A),并重建超声图像(图 1B)。然后,利用本文所提出的互相关自动测量的方法进行羽状角检测(详见1.3节),检测结果将与3位有经验临床超声医师的手动测量结果进行比较。
|
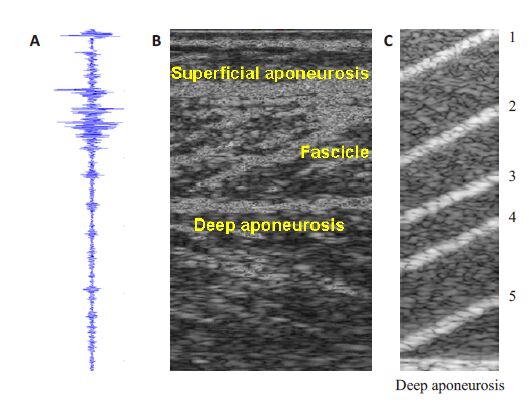
图 1 腓肠肌的超声射频信号、由射频信号重建的B-型超声图及仿真腓肠肌的超声图 Figure 1 Ultrasound radiofrequency (RF) signals (A),B-mode image of gastrocnemius musclereconstructed using RF signals (B),and a simulatedultrasound image of the gastrocnemius muscle (C). |
编写仿真程序,调用Field II程序包,设计1块40mm×10 mm×90 mm的腓肠肌体模,其中100 000个散射因子随机分布在体模内部。线阵超声探头为128晶振,中心频率为3 MHz,系统采样频率为100 MHz,然后利用Field II计算出128根反射射频信号线,图像动态显示范围压缩到40 dB。腓肠肌的仿真超声结果如图 1C所示,体模具有5 条不同角度的仿真肌束和一条仿真肌腱膜。利用本文所提出的互相关自动测量的方法进行羽状角检测(详见1.3节),测量值与仿真设计时的理论值进行比较,分析本文所提出的方法的有效性。
1.3 基于超声射频信号的互相关自动测量算法如图 1B所示,羽状肌的肌肉层中含有浅层肌腱膜、多根肌束、和深层肌腱膜,根据肌束的排列方向和深层肌腱膜的方向可以画出肌束线和深层肌腱膜线,两线的夹角即为肌束与深层肌腱膜之间的夹角,称为羽状角[14]。本文仅以跟踪一条肌束为例介绍本文所提出的羽状角测量方法。
利用Matlab7.11自编“肌肉形态分析软件”,功能主要包括射频信号读入、超声图像重建、参数选择、测量结果显示与保存等。首先,读入所采集的腓肠肌的超声射频信号(.rf文件),然后,将超声信号沿纵向方向进行降采样,沿横向方向进行插值,保证重建的超声图像与超声设备所显示的B-型超图像大小一致(340×321),如图 1B所示。选择羽状角参数,即可按照下面的互相关算法自动测量羽状角,并将结果显示在结果框中。
互相关自动测量算法
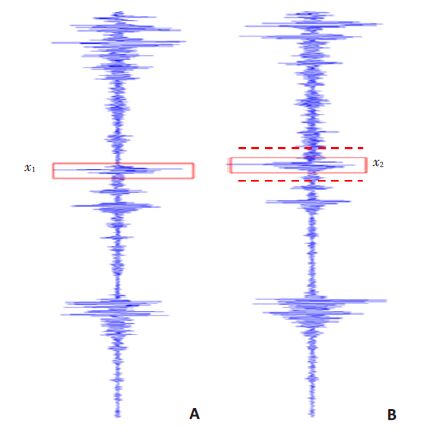
在超声图像中选择一条清晰的、长度适中的肌束作为被测肌束,在其上确定一跟踪起始点,以该点为中心沿该条信号线选取一段信号(含20个采样点)作为感兴趣的肌束信号x1 ,如图 2A所示,然后沿两侧相邻的超声射频信号线搜索与x1 相关性最大的肌束信号,搜索范围设定为以该中心点两侧各20个点的范围,如图 2B所示。公式(1)为互相关算法公式。
|
图 2 当前超声射频信号与相邻超声射频信号 Figure 2 Ultrasound RF signals of the current line and theneighbor line. A: Current ultrasound RF signals. x1presents the signal of muscle fascicle (marked by redbox); B: Adjacent ultrasound RF signals. Two dashedlines indicate the searching range (-20,20). x2 presentsthe signal with the maximum cross-correlation value. |
| ${{R}_{{{x}_{1}},{{x}_{2}}}}\left( t \right)=E{{\left( {{x}_{1}}\left( t \right) \right)}^{*}}{{x}_{2}}\left( t+\tau \right)$ | (1) |
其中,E表示期望值,x1 是当前射频信号线上感兴趣的肌束信号,x2 是相邻射频信号线的肌束信号,*表示卷积。搜索范围为(-20,20),τ表示x2 相对于x1 的位移偏移量,τ ∈(-20,20)。当R值最大时,表明x2 与x1 匹配,x2 就是所要找的肌束信号,并记录其位置[公式(2)]。
| ${{A}_{2}}={{A}_{1}}+\tau $ | (2) |
其中,A2 是相邻信号线上肌束x2 的中心位,A
然后,以这两条相邻超声射频信号为当前信号线,分别向左右方向重复上述互相关搜索过程,跟踪肌束方向。评判跟踪是否结束有两个标准:
(1)跟踪到边界,即搜索到第一条信号线或者最后一条信号线;
(2)跟踪到肌束的终点(若该点的R值远远小于前一个点的R值,则该点为肌束终点。本文设定肌束终点的R值小于前一个点的R值的1/10)。
当跟踪完成时,将各个信号线上的肌束信号位置进行线性拟合,得到跟踪目标——腓肠肌肌束线。
最后,进行深层肌腱膜线的跟踪,算法同上。公式(3)和公式(4)分别为肌束线和深层肌腱膜线的线性表达公式,由斜率值k1 和k2 便可计算肌束线和深层肌腱膜线的夹角α,即羽状角[公式(5)]。
| ${{y}_{1}}={{k}_{1}}\cdot x+{{b}_{1}}$ | (3) |
| ${{y}_{2}}={{k}_{2}}\cdot x+{{b}_{2}}$ | (4) |
| $a=\arctan \left| \frac{{{k}_{2}}-{{k}_{1}}}{1+{{k}_{1}}\cdot {{k}_{2}}} \right|$ | (5) |
本文通过计算变异系数(CV)和均方根误差(RMSE)2个统计学参数来评价本文所提出的互相关自动测量方法的可重复性。
变异系数是衡量各测量值变异程度的一个统计量,定义如公式(6):
| $CV = \frac{S}{X} \times 100\% $ | (6) |
其中,X及S分别为测量数据的样本平均数和标准差。由定义可以看出,CV是一种相对分散度的衡量指标,可以消除平均数不同对各组数据变异程度比较的影响[15]。
均方根误差的定义如公式(7):
| $RMSE = \sqrt {\frac{{\sum\limits_{i = 1}^n {d_i^2} }}{n}} $ | (7) |
式中,n为测量次数,di为第i个测量值与均值的差值。
通过绘制Bland-Altman 差值图,分析手动测量方法和互相关自动测量方法的一致性。
2 结果 2.1 仿真实验结果利用本文所提出的互相关自动测量方法检测仿真超声图中的腓肠肌肌束的羽状角,图 3A显示该算法可以很好地跟踪肌束及肌腱膜。表 1列出仿真超声图中5条肌束线与肌腱膜线之间的夹角(羽状角)和肌腱膜角度的理论值和测量值,以及两者之间的误差值。测量值的均值与理论值之间的差异在1°之内。
|
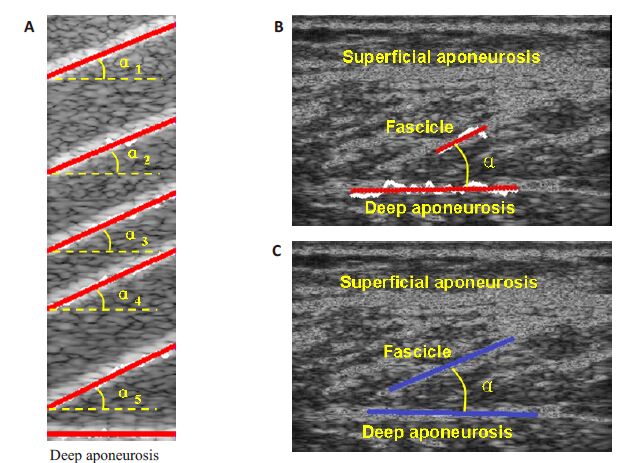
图 3 仿真超声图和人体腓肠肌超声图的肌束线和深层肌腱膜线的检测结果 Figure 3 The tracking results of muscle fascicles and deep aponeurosis. A: Five musclefascicles and one deep aponeurosis are automatically tracked (marked by red line) inthe simulated ultrasound image. The five muscle fascicle pennation angles aremarked α1-α5; B: In reconstructed ultrasound image,the muscle fascicle and deepaponeurosis are automatically detected using the proposed method (marked by redlines). The pennation angle is marked α; C: In the same ultrasound image as B,themuscle fascicle and deep aponeurosis are drawn by hand (marked by the blue lines).The pennation angle is marked by α. The white curves in A and B present the tracesdetected using the proposed method. |
| 表 1 仿真实验结果 Table 1 Results of the simulation test |
如图 3B-C及表 2所示,本文算法自动跟踪人体腓肠肌的肌腱膜线与超声医师手动绘制结果近似,而所跟踪的肌束线的长度往往要短于手动绘制结果。但是,从结果看,这对羽状角的计算影响不大,两种方法所测量的羽状角平均值的差值约为1°,手动测量的羽状角为21.49°±1.79°,自动跟踪的羽状角为20.48°±0.47°。
| 表 2 临床实验结果 Table 2 Results of the clinical test |
自动测量方法与手动测量方法所获得的两组数据的变异系数CV(2.32%,2.98%)和均方根误差RMSE(0.46°,0.61°),分析两种方法的可重复性。可看出两种方法的CV值都小于3%,RMSE均小于1°,表明互相关自动测量方法的可重复性与手动测量方法相似。
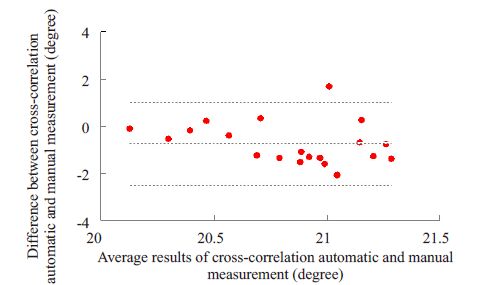
图 4显示的是Bland-Altman差值法分析结果。手动工测量和自动测量两组数据的差值均值与差值方差分别为-0.73°与0.90°,则95%一致性界限为-0.73°±1.96×0.90°,即(1.04°,-2.49°),其一致性界限较窄,且只有一个数据点落到95%一致性界限外,表明手动测量与自动测量这两种方法的一致性较良好。
|
图 4 互相关自动测量方法与手动测量方法的Bland-Altman图 Figure 4 The Bland-Altman plot of the pennation angle measuredwith cross-correlation automatic and manual measurements. |
本文结果表明,互相关自动测量方法可通过跟踪肌束的超声射频信号,在较严重的斑点噪声情况下仍可准确地跟踪腓肠肌肌束和肌腱膜的方向,自动测量腓肠肌的羽状角,与手动测量结果相差较小。羽状角的大小易受多种因素影响,例如受试者的个体差异(年龄、性别、体质量等)、测试姿势、测量位置、肌肉的健康状况、及超声设备的因素。因此,通过限制受试者的年龄体重性别,可减少受试者的个体差异对羽状角测量的影响。而由于测试姿势的不同,腓肠肌的状态不一样,会导致测量的羽状角数值有所不同。本文的受试者取坐姿,膝关节成近90°,踝关节背屈40°,腓肠肌处于拉伸状态,腓肠肌羽状角的测量值为20.48°±0.47°。这一结果与文献[17]的测量结果近似,其实验对象采取踝关节跖屈45°姿势,健侧的腓肠肌羽状角为20.38°±5.42°。最近有文献报道羽状角的动态测量,在跖屈过程中羽状角变化范围在19.3°±0.7°至35.4°±6.3°之间[18]。另有文献报道腓肠肌内侧头远端的羽状角约为13°[16],可见腓肠肌的观测位置对羽状角的影响较大。
不同的超声设备也会导致与羽状角测量结果的差异,主要原因是成像算法和图像后处理算法的差异。超声设备系统在超声成像时,会将原始超声射频信号经过降采样或插值处理后,转化为灰度图像,因此不同的成像算法就会影响到羽状角的测量结果。成像处理后,往往还要经过去噪、滤波等处理,以得到的清晰的超声灰度图像。但是,经过这些处理后超声射频信号所含有的生物组织原始信息将部分丢失[13]。本文所提出的互相关自动测量方法直接对超声射频信号进行运算,利用射频信号幅值和相位的信息,受噪声影响小。
然而,这种基于超声射频信号的互相关自动测量方法尚有不足之处,例如有些肌束纤维的连续性不好,在超声图像中呈小段显示,对于射频信号的肌肉纤维,互相关自动测量方法虽然依靠小段肌束仍可确定肌束方向,对羽状角的计算影响不大,但是会对肌束长度的测量产生较大误差,因为羽状肌的肌束长度定义为肌束从浅层肌腱膜到深层肌腱膜之间的长度[17]。因此,若增加肌束长度测量功能时,可基于本文结果,利用先验知识增大搜索范围和改进跟踪终止条件,将断开的肌束纤维连接起来,然后跟踪计算,以期提高肌束参数测量的准确性。
超声定量评价对评估肌肉功能的变化,以及对肌肉运动康复训练都有着重要的意义[2-3, 18-19]。然而,肌肉结构化参数的测量目前大多是手工标注测量,面对大量的肌肉超声图像,这样测量工作费时费力,自动测量方法的研究具有现实意义。目前,所报道的腓肠肌羽状角检测方法大多是基于超声灰度图像,通过对超声图像处理分析,自动获得肌肉的结构参数,取得了良好的效果[6-11, 17, 20-21]。而本文直接对超声射频信号跟踪肌束方向,计算羽状角,在噪声环境中也得到了较好的结果。
总之,本文提出一种基于超声射频信号的自动追踪肌束方向并测量羽状角的互相关算法,通过仿真数据和人体数据的检验,该算法的可重复性良好,与手动测量结果基本一致。本方法在较严重的噪声情况下仍可跟踪腓肠肌的肌束走向,自动测量腓肠肌的羽状角。在此研究的基础上可进一步改善以自动测量肌肉厚度和肌束长度等参数形成肌肉形态定量分析软件,用于评估肌肉功能的变化,指导肌肉运动康复的训练。
| [1] | Van Der Kooi EL, Vogels OJ, Van Asseldonk RJ, et al. Strength training and albuterol in facioscapulohumeral muscular dystrophy[J]. Neurology,2004, 63 (4) : 702-8. DOI: 10.1212/01.WNL.0000134660.30793.1F. |
| [2] | Fried GW, Fried KM. Spinal cord injury and use of botulinum toxin in reducing spasticity[J]. Phys Med Rehabil Clin N Am,2003, 14 (4) : 901-10. DOI: 10.1016/S1047-9651(03)00097-4. |
| [3] | Strasser EM, Draskovits T, Praschak M, et al. Association between ultrasound measurements of muscle thickness, pennation angle, echogenicity and skeletal muscle strength in the elderly[J]. Age (Dordr),2013, 35 (6) : 2377-88. DOI: 10.1007/s11357-013-9517-z. |
| [4] | Chleboun GS, France AR, Crill MT, et al. In vivo measurement of fascicle length and pennation angle of the human biceps femoris muscle[J]. Cells Tissues Organs,2001, 169 (4) : 401-9. DOI: 10.1159/000047908. |
| [5] | Maganaris CN, Baltzopoulos V, Sargeant AJ. Repeated contractions alter the geometry of human skeletal muscle[J]. J Appl Physiol (1985),2002, 93 (6) : 2089-94. DOI: 10.1152/japplphysiol.00604.2002. |
| [6] | Zhou Y, Zheng YP. Estimation of muscle fiber orientation in ultrasound images using revoting hough transform (RVHT)[J]. Ultrasound Med Biol,2008, 34 (9) : 1474-81. DOI: 10.1016/j.ultrasmedbio.2008.02.009. |
| [7] | Ling S, Chen B, Zhou YJ, et al. An efficient framework for estimation of muscle fiber orientation using ultrasonography[J]. Biomed Eng Online,2013, 12 (1) : 98. DOI: 10.1186/1475-925X-12-98. |
| [8] | Zhou Y, Li JZ, Zhou G, et al. Dynamic measurement of pennation angle of gastrocnemius muscles during contractions based on ultrasound imaging[J]. Biomed Eng Online,2012, 11 : 63. DOI: 10.1186/1475-925X-11-63. |
| [9] | Zhou Y, Zheng YP. Longitudinal enhancement of the hyperechoic regions in ultrasonography of muscles using a Gabor filter bank approach: a preparation for semi-automatic muscle fiber orientation estimation[J]. Ultrasound Med Biol,2011, 37 (4) : 665-73. DOI: 10.1016/j.ultrasmedbio.2010.12.011. |
| [10] | Rana M, Hamarneh G, Wakeling JM. Automated tracking of muscle fascicle orientation in B-mode ultrasound images[J]. J Biomech,2009, 42 (13) : 2068-73. DOI: 10.1016/j.jbiomech.2009.06.003. |
| [11] | Zhao H, Zhang LQ. Automatic tracking of muscle fascicles in ultrasound images using localized Radon transform[J]. IEEE Trans Biomed Eng,2011, 58 (7) : 2094-101. DOI: 10.1109/TBME.2011.2144593. |
| [12] | Luo J, Konofagou E. A fast normalized cross-correlation calculation method for motion estimation[J]. IEEE Trans Ultrason Ferroelectr Freq Control,2010, 57 (6) : 1347-57. DOI: 10.1109/TUFFC.2010.1554. |
| [13] | Lévénez M, Timmermans B and Duchateau J. Effect of myoaponeurotic crocheting of the sural triceps on passive pressure and muscle architecture during stretching[J]. Kinesither Rev,2009, 9 : 56-61. |
| [14] | Legerlotz K, Smith HK, Hing WA. Variation and reliability of ultrasonographic quantification of the architecture of the medial gastrocnemius muscle in young children[J]. Clin Physiol Funct Imaging,2010, 30 (3) : 198-205. DOI: 10.1111/cpf.2010.30.issue-3. |
| [15] | 吴冬友, 杨玉坤. 统计学[M]. 北京: 中国税务出版社, 2005 . |
| [16] | 叶攀, 胡海涛. 腓肠肌羽状角的高频超声测量及其临床意义[J]. 中华医学超声杂志: 电子版,2014, 11 (3) : 46-9. |
| [17] | Zhou GQ, Chan P, Zheng YP. Automatic measurement of pennation angle and fascicle length of gastrocnemius muscles using real-time ultrasound imaging[J]. Ultrasonics,2015, 57 : 72-83. DOI: 10.1016/j.ultras.2014.10.020. |
| [18] | 刘鹏, 王艳君, 毛玉瑢, 等. 减重步行训练改善脑卒中患者小腿肌肉形态结构的生物力学研究[J]. 中国康复医学杂志,2012, 27 (9) : 792-6. |
| [19] | 杨远滨, 张京, 冷振鹏, 等. 抗痉挛治疗前后脑卒中患者超声肌肉结构参数的比较[J]. 中国康复理论与实践,2014, 20 (7) : 641-4. |
| [20] | Kawamoto S, Imamoglu N, Gomez-Tames JD, et al. Ultrasound imaging and Semi-Automatic analysis of active muscle features in electrical stimulation by optical flow[C] //2014 36TH abbyak international conference of the ieee engineering in medicine and biology society (EMBC), 2014: 250-3. |
| [21] | Lee D, Li Z, Sohail QZ, et al. A three-dimensional approach to pennation angle estimation for human skeletal muscle[J]. Comput Methods Biomech Biomed Engin,2015, 18 (13) : 1474-84. DOI: 10.1080/10255842.2014.917294. |
 2015, Vol. 35
2015, Vol. 35
