2. 南方医科大学 生物医学工程学院信息技术系电子技术系,广东 广州 510515 ;
3. 南方医科大学 基础医学院病理 系,广东 广州 510515 ;
4. 南方医科大学 南方医院乳腺外科,广东 广州 510515
2. Department of Electronic Technology, School of Biomedical Engineering; Department of Pathology, School of Basic Medicine Nanfang Hospital, Southern Medical University, Guangzhou 510515, China ;
3. Southern Medical University, Guangzhou510515, China Nanfang Hospital, Southern Medical University, Guangzhou 510515, China ;
4. Department of Breast Surgery, Nanfang Hospital, Southern Medical University, Guangzhou 510515, China
B型超声对液体与实质性组织表现出显著的图像差别,在发现肿物、畸形、结石等引致局部结构明显形态改变的疾病方面有着明显优势,无创方便廉价实时等优点使得它在体检和医疗诊治中的应用十分广泛[1]。由于成像原理和过程中的多种因素影响,B超图像常表现出对比度较低、噪声干扰严重、边界模糊等缺点,自动分割在B超中的应用具有较大局限性。人们从多种角度采用多种方法进行B超图像的自动分割探索,如区域增长法、动态阈值分割法、模糊聚类法、分水岭法、HMM融合法、EM算法和高斯混合分布模型、小波变换法等,现有解决方案尚存在较大的改进空间。基于变分的水平集方法是近年来发展迅速的一个分支,它将图像分割问题表达为能量函数的最小化问题,由变分原理将其转化为偏微分方程的求解[1-2]。相比于传统的区域分割方法,水平集方法允许在能量函数中加入与图像内容有关的约束条件等综合信息,获得更加准确和合理的分割效果。
水平集方法的主要思想是将移动的界面作为零水平集嵌入高一维的水平集函数中,由封闭超曲面零水平集的演化方程得到水平集函数的演化方程,通过水平集函数曲面的演化来隐含地求解轮廓曲线。水平集方法可分为全局水平集、边界水平集和区域水平集三类。
以CV模型[3]为代表的全局水平集模型利用图像的全局灰度信息驱动曲线形变和移动,主要优点是当两种区域的灰度差别较大时具有较强的抗噪能力,能够有效分割出模糊边缘;对初始轮廓线位置不敏感;经理论证明能够收敛到全局最优。但是,它以图像灰度分布均匀、前景背景有明显差异为前提条件,不能直接用于B超图像的病灶分割。以GAC模型[2]为代表的边界模型利用目标边界的梯度变化信息引导曲线运行,优点是曲线在平滑区域演化很快,而在目标边界处停止运动,在低噪图像中分割准确且运算代价小,但在高噪情况下容易受到噪声干扰而使曲线停顿在错误的位置上。以RSF模型[4]为代表的区域水平集模型利用曲线内外部局部区域的拟合能量信息促使曲线形变,能够较好地处理灰度不匀的情况,但运算代价比全局和局部模型显著增加,使用的核函数的方差为定值,容易陷入局部极值解。近年来围绕RSF模型的改进主要分为两个方向:核函数的选择,如用其他函数(均值、方差)来代替高斯分布函数[5];融合其他方法,如文献[6-7]向RSF模型中加入了模糊聚类方法,在一定程度上提高了像素点的判断精度,文献[7]还提出了快速计算方案,但对复杂图像仍存在模糊度选取问题,可能造成过分割或欠分割。文献[8-10]融合了CV和RSF模型,可利用两者的优点,但双模型的计算量显著增加。
本文针对B超图像特点,利用区域水平集模型的优点,定义反映曲线像素点受到目标和背景两个区域动态权重的因子,通过概率分布估计模型计算像素点被动态权重的程度,以此为依据对像素点进行区域划分,以提高水平集曲线抗干扰能力和定位模糊边界能力;同时本文将B超图像目标分割看作对感兴趣目标区域的局部分割,将水平集的计算求解约束到局部分割范围,减少计算量,实现特定目标区域的高效提取。
1 动态权重因子的定义和融入区域水平集模型设C={ Cin,Cout}是图像I关于轮廓线C的两个划分,Cin代表轮廓线内部即目标区域,Cout代表轮廓线外部即背景区域,RSF模型的能量函数定义为:
| $ {E_{RSF}}\left( {C,{f_1}\left( x \right),{f_2}\left( x \right)} \right) = \sum\limits_{i = 1}^2 {{\lambda _i}\int_{{\Omega _i}} {K\left( {x - y} \right)\left| {I\left( y \right) - {f_i}\left( x \right)\left| {^2dy,i = 1,2} \right.} \right.} } $ | (1) |
其中,Ω1和Ω2分别为轮廓线内部和外部区域,K为核函数,一般选择为高斯函数,f1(x)和f2(x)为像素点x处的拟合值,λ1和λ2为常系数。
分析图像,在目标内部和背景内部,局部灰度分布一般是均匀的,而在目标与背景的交界处,局部灰度分布的差异性较为显著。因此,某个区域内部的灰度分布越均衡,则越应当作为一个整体被划分,即对曲线像素点的权重作用越大,曲线最后应当包绕在该区域的边界上;反之,如果某个区域内部的灰度分布不均衡即差异较大,则表明它很可能既包含了目标部分又包含了背景部分,或者带有强噪声点,曲线不应当收拢到该区域的边界上,也就是该区域对像素点的权重作用应当较小。RSF模型中轮廓线内部和外部区域的作用力的权重由常系数λ 1和λ2来规定,一则需要手工指定,依赖经验值,二则不利于动态调整。图像区域灰度分布均衡度常用的度量指标有均值、方差、熵等,其中熵(entropy)作为概率系统的不确定程度指标,当系统越确定时,熵值越小,反之,系统越不确定,熵值越大。在统计学中,熵的玻尔兹曼函数S定义为
| $ S = \kappa \cdot Ln\Omega $ | (2) |
其中,κ为(玻尔兹曼)常数,Ln为对数运算符,Ω为系统分子的状态数。
熵的概念同样可以映射到图像灰度分布的均衡性上。图像中一个区域的灰度分布越均匀,则熵值越小,反之,熵值越大。但是,熵是信息论中信息量的度量,直接引入它到图像处理中还有一些不足,因为熵不能反映图像中的几何形状、像素的空间分布等重要的处理信息[9, 12]。本文利用熵的基本含义,对它在图像处理中的定义做了修改:图像的熵表示为图像灰度级集合的比特平均数,描述了图像信源的平均信息量,即图像的信息丰富程度。设x(i, j)为图像的像素点,图像熵对应着图像分布的直方图,近似于采样均值。全局采样均值不能准确反映图像各个部分的像素分布情况和变化情况,所以,本文设计了局部熵,即局部区域采样均值,局部熵的定义为
| $ H\left( p \right) = - \sum\limits_{z \in B\left( {x,\varepsilon } \right)} {{p_x}\left( z \right) \cdot \ln \;{p_x}\left( z \right),{p_x}\left( z \right) = \frac{{\left| {\left\{ {z \in B\left( {x,\varepsilon :I\left( x \right) = z} \right.} \right\}} \right|}}{{\left| {B\left( {x,\varepsilon } \right)} \right|}}} $ | (3) |
其中,px(z)表示以像素点x为中心的半径为ε的窗口中的灰度级概率密度。局部熵比均值和方差能更有效地反映灰度阶梯变化状况。轮廓线上的像素点x受到局部熵的作用,用一个新的因子:动态权重因子来表示。动态权重因子定义为半径为ε的区域的局部熵A ε(I(x)):
| $ {A_\varepsilon }\left( {I\left( x \right)} \right) = - \sum\limits_{i,j \in {\Omega _\varepsilon }} {p\left( {i,j} \right)\ln \;P\left( {i,j} \right)} $ | (4) |
其中Ω ε为关于像素点x的半径为ε的区域,i, j为像素点x的坐标。
RSF模型的水平集表示为
| $ {{\rm{E}}_{RSF}}\left( {\varphi ,{f_1}\left( x \right),{f_2}\left( x \right)} \right)\sum\limits_{i = 1}^2 {\int_{{\Omega _i}} {K\left( {x - y} \right){{\left| {I\left( y \right) - {f_i}\left( x \right)} \right|}^2}{M_i}\left( {\varphi \left( y \right)} \right)dy,i = 1,2} } $ | (5) |
其中M1(φ)=H(φ), M2(φ)=1 -H(φ), Hε(x)为Heaviside函数,
| $ {f_i}\left( x \right) = \frac{{K\left( x \right) * \left[{{M_i}\left( {\varphi \left( x \right)} \right)I\left( x \right)} \right]}}{{K\left( x \right) * {M_i}\left( {\varphi \left( x \right)} \right)}} $ |
将(3)式代入RSF模型能量函数,用高斯函数表示核函数,得到动态权重因子区域水平集模型公式:
| $ \begin{array}{l} {{\rm{E}}_A}\left( {C,{f_1}\left( x \right),{f_2}\left( x \right)} \right)\sum\limits_{k = 1}^2 {{{\left( { - 1} \right)}^{k + 1}}\int_{{\Omega _k}} {{G_\varepsilon }\left( {x - y} \right){A_\varepsilon }\left( {I\left( x \right){{\left| {I\left( y \right) - {f_i}\left( x \right)} \right|}^2}dy} \right.} } \\ \;\; = \sum\limits_{k = 1}^2 {{{\left( { - 1} \right)}^k}\int_{{\Omega _k}} {{G_\varepsilon }\left( {x - y} \right)\left( {\sum\limits_{i,j \in {\Omega _\varepsilon }} {p\left( {i,j} \right)\ln p\left. {\left( {i,j} \right)} \right){{\left| {I\left( y \right) - {f_i}\left( x \right)} \right|}^2}dy} } \right)} } \end{array} $ | (6) |
其中,G ε(I(x))为以像素点x为中心半径为ε的区域内的高斯分布,Ω1和Ω2分别为轮廓线内部和外部的区域。
可以看到,(6)式中的两项分别为像素点受到曲线内部和外部区域的动态权重力,方向相反,当二力相等时(6)式能量函数EA达到最小值,此时水平集停止在目标和背景的边界上,得到分割轮廓线。动态权重因子的作用相当于一个变化的系数,随着轮廓线形变和位移到图像的不同区域,动态调节两项力的大小,促使轮廓线较快地向目标边界移动和形变。
引入水平集表示法,得到动态权重因子水平集演化方程:
| $ \frac{{\partial \varphi }}{{\partial t}} = \partial \left( \varphi \right)\left[ {\sum\limits_{k = 1}^2 {{{\left( { - 1} \right)}^k}\int_{{\Omega _1}} {{G_\varepsilon }\left( {x - y} \right)(\int\limits_{{\Omega _\varepsilon }} {p\left( {i,j} \right)\ln p(i,j)){{\left| {I\left( y \right) - {f_i}\left( x \right)} \right|}^2}dy} } } } \right] $ | (7) |
其中
区域水平集模型将图像中的所有目标分割出来,计算量很大。本文根据B超图像病灶的分割要求,将初始轮廓设为一个接近并包绕B超图像目标的闭合曲线,为简便起见,统一采用手工勾勒包围目标规则图形(矩形、椭圆形或圆形)。为提高计算效率,本文采用局部计算方案,定义基于局部近似符号距离函数,放宽对初始水平集函数的要求,不再要求初始水平集必须是符号距离函数。如果直接对轮廓线上的每个像素点都做对数及求和运算,求解水平集式需要离散化迭代实现求解偏微分方程,计算量很大,因此采用局部计算思路以减少运算量和运算时间。本文采用改进的FTC(Fast two-cycle)算法[10-11],在不用求解偏微分方程的基础上近似实现水平集函数的进化,定义局部近似符号距离函数(LASDF)为
| $ \varphi \left( {x,y} \right) = \left\{ {\begin{array}{*{20}{c}} {d,点x为外部点}\\ {1,点x为轮廓线外邻域点}\\ {0,点x在轮廓线上}\\ { - 1,x为轮廓线内邻域点}\\ { - d,点x为内部点} \end{array}} \right. $ | (8) |
LASDF确定当前像素点到水平集曲线的最短距离和该距离的符号(曲线内为负,曲线外为正),计算过程只关注包绕水平集曲线的一条半径为d(宽度为2d)的狭窄带区,由于d≪n,所以可将计算复杂度由O(n2 ln S)减少为O(nd ln S),n为图像中的像素点数,S为计算每一个像素点到水平集曲线的最短距离的耗费。水平集迭代过程伪代码如下:
function phiy=activecontourCV (u0, center, d, side, d_it, m_it, m_name)
%输入图像为double型,灰度为0-255
%水平集初始化为椭圆形,center为轮廓线原点,d为窄带半径,side=1表示目标在起始轮廓线内,=0表示在外
%初始化参数
ITERATIONS=2000; %迭代次数
delta_t=0.1; %时间步长
%轮廓内外能量参数
lambda1=1; lambda2=1; nu=0; d=3;
%曲率项参数
h=1; h_sq=h^2; epsilon=1; mu=0.01 * 255^2;
%初始化LASDF
phi=initLASDF (size (u0), center, d, side);
for ii=1: ITERATIONS;
%显示并保存图像
if (mod (ii-1, d_it)==0)
segim=createim (u0, phi);
imshow (segim);
segim=createim (u0, phi);
filename=strcat (m_name, sprintf ('%d', ii, '.jpg');
imwrite (segim, filename);
end;
dirac_delta_t=delta_t * diracfunction (phi, epsilon);
%计算轮廓线内外能量
[inside, outside]=calcenergyf (u0, phi, epsilon);
energy_term=-nu -lambda1.* inside + lambda2.* outside;
dx_central=(circshift (phi, [0, -1])-circshift (phi, [0, 1]))/2;
dy_central=(circshift (phi, [-1,0])-circshift (phi, [1,0]))/2;
abs_grad_phi=(sqrt (dx_central.^2 + dy_central.^2) +0.00001);
x=dx_central./ abs_grad_phi;
y=dy_central./ abs_grad_phi;
grad_term=(mu / h_sq).* divergence (x, y);
phi=phi + dirac_delta_t.* (grad_term + energy_term);
phiy (:, :, ii)=phi;
end;
%检测零水平集的位置
function front=isfro (phi)
[n, m]=size (phi);
front=zeros (size (phi));
for i=2: n-1;
for j=2: m-1;
maxVal=max (max (phi (i:i+1, j:j+1)));
minVal=min (min (phi (i:i+1, j:j+1)));
front (i, j)=((maxVal>0) & (minVal < 0)) | phi (i, j)==0;
end
end
%初始化水平集函数,局部近似符号距离函数
function phi=initLASDF (imsize, center, d, side)
m=imsize (1); n=imsize (2);
phi=zeros (imsize);
for i=1:m;
for j=1:n;
distance=sqrt (sum ((center-[i, j]).^2));
phi (i, j)=distance-d;
if (side==0)
phi (i, j)=-phi (i, j);
end
end
end
% dirac
function y=diracfunction (x, epsilon)
y=(1./ pi).* (epsilon./(epsilon.^2+x.^2));
%求轮廓内外能量
function value=heavisidef (z, epsilon)
value=0.5.* (1+(2./pi).* atan (z./epsilon));
function[inside, outside]=calcenergyf (u0, phi, epsilon)
H_phi=heavisidef (phi, epsilon);
H_phi_minus=1-heavisidef (phi, epsilon);
A=calcuProb (d);
c1=A.*sum (sum (u0.* H_phi))/ sum (sum (H_phi));
c2=A.*sum (sum (u0.*H_phi_minus))/sum (sum (H_phi_minus));
inside=(u0-c1).^2;
outside=(u0-c2).^2;
3 结果分割实验待测图像来自南方医科大学附属医院影像库,通过对相同B超图像样本进行分割来检验本文模型的效果,并与几种水平集模型进行比较。编程平台为Matlab7,计算机配置为Intel? CoreTM(2) Duo CPU. 3.0 GHz,2 GB RAM,Windows XP操作系统。所有实验采用相同的终止阈值△E=10-4或最大迭代次数2000(考虑到用户等待时间)。图 1~3为实验结果举例,比较CV模型[2]、RSF模型[4]、SLGS模型[9]、LGF模型[10]、本文模型和专业医师手工分割结果。所有模型均按原文献方法进行相应参数设置,其中公共参数:时间步长△t=0.1,空间步长△h=1,长度惩罚项参数μ=0.01 * 255^2~0.1 * 255^2,邻域半径ε根据图像内容调整为最合适值(为5或7),尽可能达到每种模型最优的分割效果。本文方法中的窄带半径d取3,即计算水平集曲线内外各3个像素的LASDF。
|
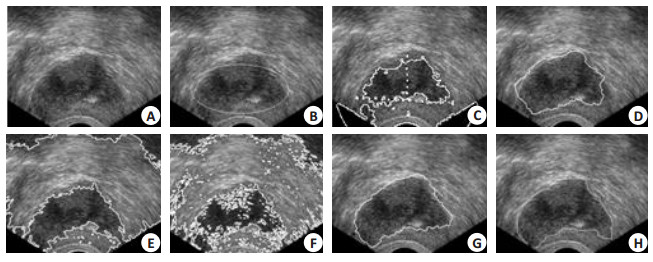
图 1 分割测试1 Figure 1 Segmentation test 1. A: Sample image to be segmented; B: Initial contour by manual; C: Segmentation result by CV model; D: Segmentation result by RSF model; E: Segmentation result by SLGS model; F: Segmentation result by LGF model; G: Segmentation result by the proposed model; H: Result of manual segmentation. |
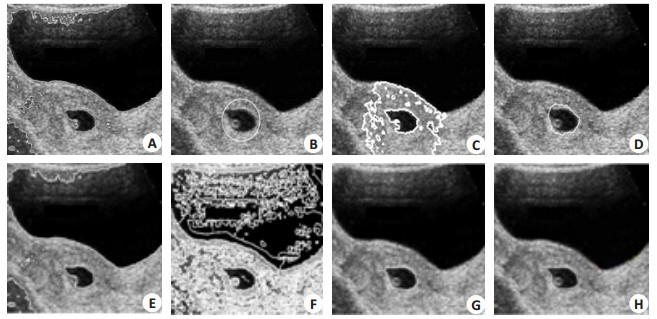
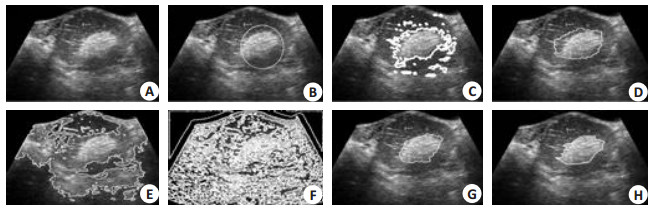
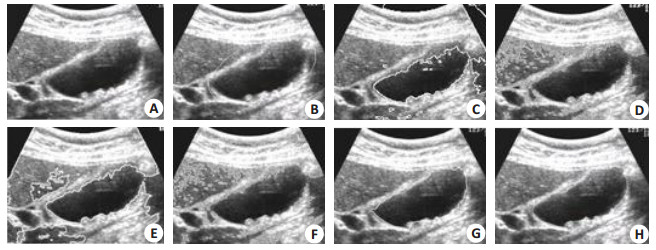
图 1A子图为待测样本390*290像素的前列腺增生B超图像,分割目标为中下部团块暗区。图 2A子图为待测样本488*415像素的盆腔(卵巢)B超图像,分割目标为中下部的卵黄囊部分。图 3A子图为待测样本615*369像素的盆腔(子宫肌瘤)B超图像,分割目标为中部偏右的子宫肌瘤体。图 4A子图为待测样本361* 252像素的胆囊B超图像,分割目标为中部横向暗色团块区域。待分割图像均存在明显的灰度分布不匀,存在不同数量的多处伪影,存在散布的不同强度的噪声杂质,病灶部分边界比较模糊。
|
图 2 分割测试2 Figure 2 Segmentation test 2. A: Sample image to be segmented; B: initial contour by manual; C: Segmentation result by CV model; D: Segmentation result by RSF model; E: Segmentation result by SLGS model; F: Segmentation result by LGF model; G: Segmentation result by the proposed model; H: Result of manual segmentation. |
|
图 3 分割测试3 Figure 3 Segmentation test 3. A: Sample image to be segmented; B: initial contour by manual; C: Segmentation result by CV model; D: Segmentation result by RSF model; E: Segmentation result by SLGS model; F: Segmentation result by LGF model; G: Segmentation result by the proposed model; H: Result of manual segmentation. |
|
图 4 分割测试4 Figure 4 Segmentation test 4. A: Sample image to be segmented; B: initial contour by manual; C: Segmentation result by CV model; D: Segmentation result by RSF model; E: Segmentation result by SLGS model; F: Segmentation result by LGF model; G: Segmentation result by the proposed model; H: Result of manual segmentation. |
根据医学诊断特异性的标准采用4个精度指示器:真阳性率(TP),假阳性率(FP),假阴性率(FN),真阴性率(TN),结合临床诊断要求定义4个分割精度指标:
可接受率accept rate:由专业医师判断自动分割结果是否可接受(含经过后续处理),是否有参考价值。
测准度
灵敏度
特异度
表 1为5种模型处理图 1~4的迭代次数、耗时和分割精度指标。对于分割结果存在多个连续区域的,取最大的区域或医师手工指定的区域。分割失败案例的指标无法计算,用“-”表示。
| 表 1 5种模型的迭代次数、耗时(秒)和分割精度比较 Table 1 Comparison of 5 models in iteration times, time consumption (seconds) and segmentation precision |
从南方医院临床医学影像图像库中随机抽取20幅B超图像,用5种模型分别进行处理,以获得处理精度的统计结果(只取全部分割成功的结果)。由于各幅图像大小、内容和质量不一致,所以不进行迭代次数和耗时的比较,只进行处理结果精度的统计比较,结果见表 2。
| 表 2 5种模型对20幅随机图像的平均分割精度比较 Table 2 Comparison of average segmentation precision of 20 random images by 5 models |
从以上实验及统计数据可以得出结论:在分割精度方面,本文模型不同程度地优于其它模型,各次实验的可接受率与CV、PSF模型相当,基本上可全部被人工接受,而平均测准度、平均灵敏度和平均特异度几乎都高于其他模型,其他模型的总体分割精度排序依次是:RSF模型、CV模型、SLGS模型和LGF模型,后两种模型效果受B超图像内容或质量的影响较大,均有分割不成功的样本。表明本文模型较为适合分割B超病变组织,同时筛检非病灶的能力较强。分析原因,CV模型借助全局信息提高了抗噪能力,但未考虑局部区域信息,水平集曲线粗略逼近目标边界,无法准确分割灰度不匀、伪影干扰和目标背景差别小的目标,且需要对所有图像点进行迭代计算,耗时较多;RSF模型运用局部拟合信息能够较好反映区域图像属性,在初始轮廓接近目标时分割较为准确,但依靠常数权重确定形变作用的比例关系,不能准确反映曲线位于不同区域时的动态变化,对模糊边界和噪声点容易出现错误;SLGS模型能够较好地提取弱边界,又有一定的抗噪性,但由于采用了全局分割策略,所以无法剔除背景中与病灶相似的成分,导致较多的碎片结果和误判断;LGF模型通过小邻域高斯函数能够较准确地表现局部的不规则变化,但容易产生大量冗余轮廓碎片而无法连成完整区域;本文方法在RSF模型的基础上引入图像熵的作用,计算动态权重因子,能够根据曲线不同时刻的变化位置实时调节作用力的权重,更为合理地判断弱边界上像素点的归属,并且具有一定的抗噪能力,分割结果最接近专业医师的手工分割结果,效果最好。
在运算代价与分割速度方面,本文模型迭代次数多于SLGS模型和LGF模型,少于CV模型和RSF模型,实验耗时在部分情况下仅比LGF模型略多,比其他模型均有明显减少,说明本文模型的计算法则以及局部计算方案具有一定的降低计算复杂度的能力,有效地减少了总计算量。
5 结论本文提出一种面向B超图像病灶分割的动态权重因子区域水平集方法,利用图像熵计算动态权重因子,动态更新轮廓线内外区域对像素点的动态权重作用,决定曲线移动方向和形变趋向。在计算方法上,不采用传统的解偏微分方程方法,不需要扫描整个图像,仅对轮廓曲线内外邻域点实行转换判断处理,更新水平集演化趋势,减小了计算量。与几种水平集模型的比较,本文模型在平均测准度、平均灵敏度和平均特异度方面都表现较好,并且起伏很小,不容易受图像内容和质量的影响,较好地解决了B超图像灰度分布不匀、低对比度和模糊边界的问题。本文方法的局限性是动态权重因子是依据区域灰度分布进行计算的,而人眼视觉注意机制的研究表明,对人眼影响较大的低层视觉显著性特征还包括亮度、对比度、目标区域大小、目标位置、目标形状等,今后将根据不同内容的图像和不同需求的分割任务探索多种描述算子的表达和融合,以实现面向应用需求的更好分割。
| [1] | Saini K, Dewal ML, Rohit M. Ultrasound imaging and image segmentation in the area of ultrasound: a review[J]. International Journal of Advanced Science and Technology,2010, 24 (2) : 41-60. |
| [2] | Saini K, Lee LK, Liew SC, et al. A review of image segmentation methodologies in medical image[M]. Advanced Computer and Communication Engineering Technology Lecture Notes in Electrical Engineering, 2015 : 1069 -80. |
| [3] | Chan TF, Vese LA. Active contours without edges[J]. Image Processing, IEEE Transactions on,2001, 10 (2) : 266-77. DOI: 10.1109/83.902291. |
| [4] | Li C, Kao CY, Gore JC, et al. Minimization of region-scalable fitting energy for image segmentation[J]. IEEE Trans Image Process,2008, 17 (10) : 1940-9. DOI: 10.1109/TIP.2008.2002304. |
| [5] | Christos PL. A review of ultrasound common carotid artery image and video segmentation techniques[J]. Medical & Biological Engineering & Computing,2014, 52 (12) : 1073-93. |
| [6] | Shyu KK, Pham VT, Tran TT, et al. Global and local fuzzy energybased active contours for image segmentation[J]. Nonlinear Dyn,2012, 67 (2) : 1559-78. DOI: 10.1007/s11071-011-0088-1. |
| [7] | Alipour S, Shanbehzadeh J. Fast automatic medical image segmentation based on spatial kernel fuzzy c-means on level set method[J]. Mach Vis Appl,2014, 25 (6) : 1469-88. DOI: 10.1007/s00138-014-0606-5. |
| [8] | Liu RJ, He CJ, Yuan Y. Active contours driven by local and global image fitting energy[J]. 计算机辅助设计与图形学学报,2012, 24 (3) : 364-71. |
| [9] | Zhang KH, Zhang L, Song HH, et al. Active contours with selective local or global segmentation: A new formulation and level set method[J]. Image Vis Comput,2010, 28 (4) : 668-76. DOI: 10.1016/j.imavis.2009.10.009. |
| [10] | Wang L, He L, Mishra A, et al. Active contours driven by local Gaussian distribution fitting energy[J]. Signal Processing,2009, 89 (12) : 2435-47. DOI: 10.1016/j.sigpro.2009.03.014. |
| [11] | 潘改, 高立群, 赵爽. 基于局部熵的主动轮廓模型[J]. 中国图象图形学报,2013, 18 (1) : 78-85. |
| [12] | Mitiche A, Ayed IB. Variational and level set methods in image segmentation[M]. New York: Springer, 2010 : 105 -7. |
| [13] | Goldstein T, Bresson X, Osher S. Geometric applications of the split bregman method: segmentation and surface Reconstruction[J]. SIAM J Sci Comput,2010, 45 (1/3) : 272-93. |
| [14] | Estellers, V, Zosso, et al. Efficient algorithm for level set method preserving distance function[J]. UCLA CAM Report,2011 : 11-58. |
 2015, Vol. 35
2015, Vol. 35