冠状动脉粥样硬化是心血管疾病的主要病理基础，血管内超声（intravascular ultrasound, IVUS）是一种基于导管的成像技术，实时提供冠脉血管的截面图像^[1]。图像分辨率高，能准确获取冠状动脉的管壁厚度、管腔形态及动脉粥样硬化斑块成分等信息。在辅助诊断冠脉粥样硬化方面，IVUS已经发展成为传统冠状动脉造影（CAG）非常重要的辅助工具。然而，由心脏运动所引起的运动伪影给IVUS序列血管面积、血管容积、管腔面积、管腔容积、管腔最大最小直径、管腔面积狭窄率、斑块负荷等诊断指标的定量分析带来很大的困难，影响临床冠心病的诊断和治疗^[1-3]。

运动伪影在IVUS图像序列中表现非常显著，在纵切图上，IVUS图像序列呈锯齿状分布（如图 6上部所示）。ECG门控法是传统的抑制运动伪影的方法，分为在线（on-line）门控^[4]和离线（off-line）门控^[5]。在线ECG门控法在每个心动周期的R波处采集图像，需要结合专门的硬件设备，导管介入时间长。离线ECG门控同时采集ECG信号和IVUS图像，医生对照ECG信号从IVUS序列中标记出门控帧，介入时间减少，缺点是难以选择最佳采样点，主观性强。临床上难以同时获得ECG信号和IVUS信号^[6]。因此，近年来，研究者们致力于利用IVUS图像序列本身来寻找门控序列，即基于图像的门控法^[6-12]。基于图像的门控法完全利用图像处理技术，提取反映IVUS图像的显著性特征量作为参考点，参考点随着图像序列变化，形成一个类似ECG的时间变化信号。据此将IVUS图像分为心脏舒张末期图像和非心脏舒张末期图像两类，由关键帧组成门控序列。所谓的关键帧定义为心脏舒张末期采集到的IVUS图像。在心动周期中，舒张末期心室进入等容收缩期，心脏运动较慢，超声探头和管腔的相对位移小，此时的IVUS图像具有很好的稳定性和一致性^{[9, 13]}。目前已有的基于图像的门控方法有：以像素点局部灰度均值^[6]，感兴趣区域（ROI，人工设定）的平均灰度和绝对灰度差^[7]，管腔轮廓线^[8]等局部信息作为特征的方法。文献[6]提出的方法对带通滤波器参数敏感，难以提取心律不齐患者的IVUS序列门控帧，文献[7-8]提出的方法都需要精准的边缘检测方法，然而目前尚未存在有效的IVUS图像分割方法，降低了特征精度。文献[9]提出一种基于图像的“理解（Intelligate）”的门控方法，选择图像互相关系数，空频域特征等全局特征作为特征信息，缺点是难以准确选择主要特征。为了降低对特征提取与选择的要求，研究者利用同序列中不同帧之间的非相似性程度作为特征信息^[10-12]，构造差异矩阵，采用动态规划（dynamic programming, DP），在差异矩阵中搜索一条累计差异值最小的路径，提取出心脏舒张末期门控帧，算法复杂，计算量大。

图 6(Figure 6)

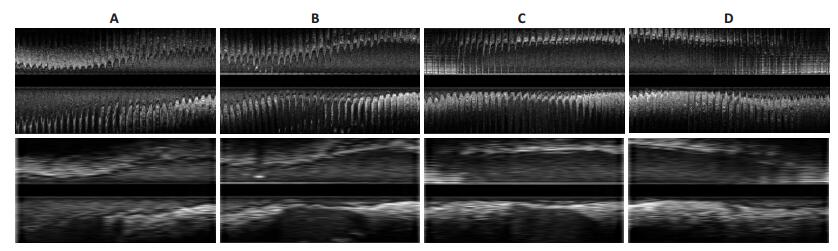
图 6 同一组序列不同方向（0°（A），45°（B），90°（C），145°（D））的原始和门控序的纵切图 Figure 6 An original IVUS set longitudinal cuts at different angles (0°, 45°, 90°, 145°) and its gated cuts.

流形学习是一种非线性降维方法，将高维非线性数据映射到低维流形，同时保持了数据集的固有属性，在图像处理中得到广泛应用^[14]。在门控方面，流形学习已用于IVUS心脏门控^[15]、4D超声^[16-17]、MRI图像的呼吸门控^[17]。本文提出一种基于流形学习的关键帧门控方法，在流形学习的指导下，将高维非线性的IVUS数据集降到低维流形中，利用低维流形中的特征向量，构造一个特征明显的距离函数，来反映心脏运动规律，检索距离函数局部最小值，将关键帧从IVUS图像中提取出来，组成门控序列。通过对门控前后序列的血管面积、血管容积、管腔面积、管腔容积、斑块负荷等量化指标的定量比较分析，以及门控前后序列纵切图分布和与已有的方法比较来评价本文算法。

在IVUS图像序列采集过程中，心脏周期性搏动引起超声探头与血管之间的相对位移、短轴方向上的平面振荡、血管尺寸连续变化、冠脉血管部分位置重采样或未采样等，在IVUS纵切图像上产生锯齿形状的运动伪影。但这些变化都是缓慢平滑的，且同一相位处的IVUS图像具有很高的相似性。因此，IVUS图像序列处于一个环绕空间（ambient space）的低维平滑流形上，每一帧图像代表高维空间中的一个样本点。IVUS图像序列具有数据量大、维数高、非线性的特点，一幅图像中包含成千上万的图像特征。心脏运动只需用几个基本参数描述就能实现，有效选择反映心脏运动的特征参数是本文的重要内容。本文采用拉普拉斯特征映射算法（laplacian eigenmap，LE）对IVUS序列图像进行降维，LE算法保持了数据流形内在的几何特性，求解过程可转化为对稀疏矩阵的特征分解问题，计算简单。

拉普拉斯特征映射算法的基本思想是利用图的谱理论，寻找某种意义上最优地保持局部邻域信息的低维表达，使得在高维空间中距离近的点在映射到低维流形后它们之间的距离仍旧很近^[18]。给定高维空间${\Re ^N}$中的一组样本点X={x₁, ..., x_n}，寻找低维空间${\Re ^t}\left( {N \gg t} \right)$中的一组点Y={y₁, ..., y_n}，用低维y_i描述高维x_i。LE算法主要由三个步骤组成：

（1）选择邻域，构建局部邻域图G。计算每个样本点x_i和其余样本点之间欧氏距离，如果样本点x_i和x_j是近邻点，则图G有边x_ix_j。可采用以下两种方法确定邻域：

①k-nn算法：如果x_j是x_i的k近邻点或者x_i是x_j的k近邻点，则x_i和x_j有边连接；

②ε-ball算法：若x_i与x_j的距离小于ε，则点x_i和x_j有边连接，与x_i相连接的点都是其近邻点。

（2）选择权值W。在邻域关系图G中，设置权值，有以下两种方法：

①高斯核方法：$W = \left\{ {\begin{array}{*{20}{l}} {{e^{-\frac{{{{\left\| {{x_i}-{x_j}} \right\|}^2}}}{\lambda }}}, {x_i}{\rm{与}}{x_j}{\rm{近邻}}, {\rm{其中}}\lambda {\rm{为一个调节参数；}}}\\ {\;\;\;\;0\;\;\;\;\;, {\rm{其他}}} \end{array}} \right.$

②简单核方法：$W = \left\{ \begin{array}{l} 1\;\;\;\;, {x_i}{\rm{与}}{x_j}{\rm{近邻}}\\ 0\;\;\;\;, 其他 \end{array} \right.$。

（3）特征映射，最小均方误差，计算样本的低维嵌入。为保持数据的局部近邻关系，最小化误差函数：

在YDY^T=I约束下，公式（1）可转化为广义特征值的求解问题

公式（2）中，L=D -W为拉普拉斯矩阵，${D_{ii}} = \sum\limits_j {{W_{ij}}} $，Y为L的前t个不为零的最小广义特征值对应的广义特征向量组成的矩阵。

在LE的指导下，提取原始序列关键帧，主要过程为：（1）坐标转换。将直角坐标下的IVUS图像转换到极坐标下，去除非成像区域信息，减少计算量；（2）LE降维。采用LE算法，将高维的IVUS数据集降到低维流形中，提取低维特征向量；（3）距离函数构造。利用选择的特征向量构造一个距离函数，反映心脏的运动规律；（4）提取关键帧。检索距离函数的局部最小值，将关键帧从IVUS图像中提取出来，组成门控序列。

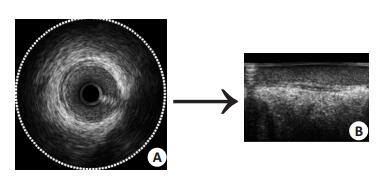
流形学习的第一步是构造邻域距离矩阵，要求对所有的数据进行存储。对于一组像素为512×512，长度为1024的IVUS图像序列，所占用的内存空间是2 GB，这对计算机存储空间和程序运行时间的损耗都是很大的。首先对图像进行坐标转换，将IVUS图像转换到极坐标下存储运算。同一组序列，极坐标下占用的内存为0.7031 G，只占直角坐标系下容量的35%。统计直角坐标系和极坐标下LE降维后，其特征向量之间的绝对误差仅是0.9%。因此，对IVUS图像序列进行极坐标转换后，既能保持原有的特质，又能减少计算机负担。图 1为IVUS图像坐标转换图，A为直角坐标系下的IVUS图像，B为对应的极坐标图像。

图 1(Figure 1)

图 1 IVUS图像坐标转换 Figure 1 Coordinate conversion for an IVUS image.

在一组包含多个心动周期，长度为n的IVUS图像序列u={u₁, ..., u_n}中，对每一帧图像u_i，希望寻找一个特征向量ϕ_i来描述反映u_i的心脏运动规律信息。利用流行学习理论，令原始高维空间x_i=u_i，低维流形空间y_i=ϕ_i。高维空间的维数N等于整幅图像像素，低维流形的维数为t。这样，流形学习m表示为：

在心脏周期中，每一帧图像用一个列向量表示，代表高维空间中的一个点，随着心脏的运动，序列图像沿着高维空间或低维流形周期性地变化。应用流形学习降维最基本的问题是维持局部信息的一致性，使得相似的图像在低维流形中有相邻的分布。心脏运动信息包含在拉普拉斯矩阵L的前t个非零的最小广义特征值所对应的特征向量中。

邻域选择是LE算法的关键内容，目前已有的多数邻域选择算法只适应于数据点分布均匀的流形，对于结构复杂的流形不能自适应的选择合理的邻域，主要依据经验来选择邻域大小。本文采用k-nn邻域算法，选择邻域k> n_cycle，n_cycle为一个心动周期内的IVUS图像帧数。IVUS图像序列的欧氏距离矩阵呈一定的周期性，这个周期就是心脏运动的周期n_cycle。图 2为同一组IVUS图像序列的前200帧（A），前1024帧（B）图像的欧氏距离矩阵，灰度值越低，表明图像的距离越近。由患者的心率f_c来确定n_cycle，f_c选择过程如下：（1）图像u_i的欧氏距离函数为E_i（图 2中第i行或者第i列），对E_i做傅里叶变换，E_i的幅度谱在正常心率范围内（50-140 beats/min）的峰值所对应的频率就是图像u_i估计得到的心率f_i；（2）所有图像估计得到的心率均值即为心率估计值：${f_c} = \frac{1}{n}\sum\limits_{i = 1}^n {{f_i}} $。这样，一个心动周期内的IVUS图像帧数为：n_cycle=round(f_sam/f_c)，f_sam为每分钟采集IVUS图像的帧数。

图 2(Figure 2)

图 2 同一组IVUS序列前200帧（A），1024帧（B）图像的欧氏距离矩阵 Figure 2 Visualization of the euclidean distance matrix from the first 200 frames (A) and 1024 frames (B) of an IVUS set.

LE算法的另一个主要内容是低维流形的维数t的确定，目前还没有固定的方法指导低维维数的选择。本文实验表明，对IVUS图像序列LE降维，当t大于4时，对距离函数影响不大，因此本文选择内蕴维数t=4。

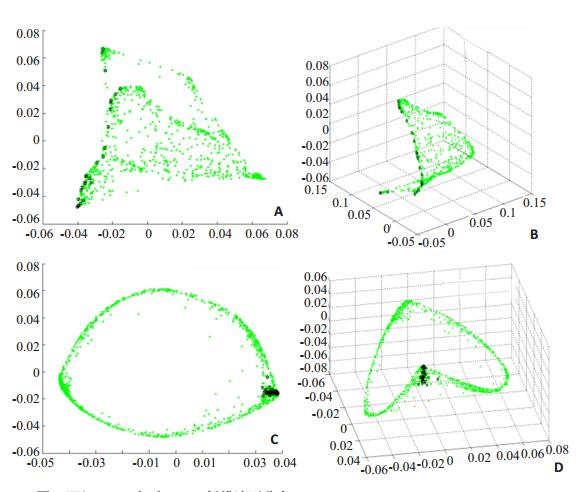
利用LE算法对IVUS图像序列降维，IVUS序列在低维流形中的分布主要有两种情况，如图 3所示。图 3为两组IVUS序列降低到2D、3D空间的分布图，“绿色圆实点”是图像在低维流形中的分布，“黑色六角星符”是文献[6]方法寻找到的关键帧的分布。图 3上部虚框内对应的IVUS图像序列血管结构变化大，序列进展方向上出现斑块且血管面积变化大，低维流形中关键帧分布离散；图 3下部黑色虚框内对应的IVUS图像序列血管结构变化不明显，无斑块，序列进展方向上血管面积变化小，低维流形中关键帧分布集中。统计13组临床IVUS图像序列，其中10组序列低维分布属第一种情况，另3组序列低维分布属第二种情况。可见，在低维流形中，仅用样本点分布的聚类性质很难寻找关键帧。文献[15]将低维流形中前后帧欧式距离函数的局部极大值作为关键帧所处位置，但欧式距离函数特征不明显，容易漏检或误检关键帧。根据心脏运动的特点，心脏舒张末期的IVUS图像稳定，相邻帧之间的差异性小。本文构造距离函数来提取关键帧，距离函数定义为：

图 3(Figure 3)

图 3 两组IVUS序列2D、3D低维流形分布 Figure 3 2D and 3D manifold of two IVUS sequences.

公式（4）中，d_s(i -s, i + s)为降维后图像u_{i -s}与u_{i + s}的欧氏距离，即d_r(i -s, i + s)=║ϕ_{i + r} -ϕ_i║，ϕ_i为原始图像u_i在低维流形中的映射，w_s为权重值，取w_s=e^-s2/(2δ2)，δ为常数，m为正整数，取$m = round\left( {\frac{1}{4}{n_{cycle}}} \right)$。

归一化公式（4），得到最终的距离函数表达式：

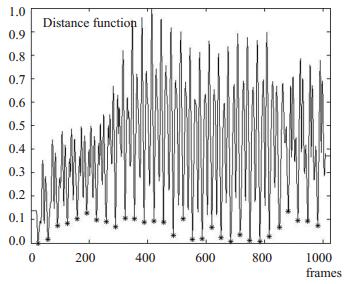
在一个心动周期中，当u_i处于心脏舒张末期时，距离函数值达到最小。图 4为一组长度为1024的IVUS图像序列距离函数曲线，在一定程度上反映了心脏周期性的运动规律。

图 4(Figure 4)

图 4 一组IVUS图像序列距离函数曲线 Figure 4 Distance function of an IVUS sequence.

距离函数的局部最小值对应序列图像关键帧的位置，本文采用以下方法寻找距离函数局部最小值：

（1）搜索起始点。以距离函数d的最小值作为搜索起点p_start；（2）向前搜索局部最小值。以p_start为搜索起点，n_cycle为搜索步长。round(0.4 × n_cycle)为窗宽，向前搜索上一个局部最小值点p_{start -1}。再以p_{start -1}为新的起点，寻找p_{start -1}的上一个局部最小值点p_{start -2}，重复此过程，直到向前搜索完毕；（3）向后搜索局部最小值。类似（2）的方法，以p_start为起点，向后搜索局部最小值点；（4）所有局部最小值点位置上的图像构成关键帧，形成门控序列。

图 4中，“星号”点为检索到的距离函数局部最小值，即关键帧图像所在位置。

临床实验数据来源于南方医院7名患者（4男3女，年龄62±9岁，图像915±142帧，血管长度25.24±2.37 mm，像素512 × 512，256阶灰度），13组IVUS图像序列。数据采集设备是是波士顿科学公司的iLabTM Ultrasound Imaging System，超声探头为机械式旋转型，频率40 MHz，回撤速度0.5 mm/s，采样频率为30帧/s。实验平台采用个人计算机（CPU：英特尔第三代酷睿i3-3240 @ 3.40 GHz双核，4 G内存），Matlab2011a编程。

临床诊断和治疗冠心病，常用到的诊断指标中，血管容积、管腔容积、斑块负荷、面积狭窄率是几个最重要的参数，这些参数的定量计算需要检测外弹力膜（external elastic membrane, EEM）界面和管腔内膜（lumen-intima）界面，EEM界面近似为血管壁，管腔内膜界面近似为管腔边界。但目前未存在精准的提取这两个界面的方法，在临床医生的指导下，人工标记这两个界面。EEM界面可近似为椭圆^[19]，在IVUS图像中标记EEM的八个边界点，最小二乘拟合出椭圆的一般方程，以确定血管面积及血管最大最小直径。管腔内膜界面不能用确定的模型模拟，人工标记管腔边界。管腔中心定义为^[20]：

公式（6）中，[μ_i, ν_i]为边界点的坐标，N为管腔/内膜边界点数，以此来确定管腔面积、最大最小直径。结合两界面参数获得斑块负荷等血管参数。原始序列和门控序列血管容积分别定义为：

公式（7, 8）中，L, l分别是原始序列和门控序列的帧数，S_oV(i)，S_gV(i)分别是原始序列和门控序列第i帧图像的血管横截面积，d为一帧图像对应的血管厚度，本文d=1/60(mm)，h(i)为相邻门控帧之间的帧距。原始序列和门控序列管腔容积的计算类似。

斑块负荷定义为：

公式（9）中，S_v为血管横截面积，S_l为管腔横截面积。

在临床医生的指导下，人工勾画13组IVUS图像序列的EEM界面和管腔内膜界面。计算门控前后序列的血管容积、管腔容积、平均斑块负荷；检验原始序列和门控序列这三个参数的差异显著性；对每一组IVUS原始序列和门控序列的血管横截面积方差、管腔横截面积方差进行右边检验。参数差异显著性检验采用配对秩和检验方法。原始和门控序列血管横截面积方差右边检验方法是：设原始序列和门控序列的血管横截面积序列分别为X，Y，方差δ₁²，δ₂²。做出检验假设，原假设H₀：δ₁²>δ₂²，备择假设H₁：δ₁²≤δ₂²。先对X，Y的分布进行k检验，检验它们是否符合正态分布；若X，Y都符合正态分布，再对这两个正态分布的方差进行右边检验（F检验）。管腔横截面积方差的右边检验类似。实验统计结果如表 1所示，门控序列的血管容积，管腔容积显著小于原始序列。同时，门控前后的平均斑块负荷无显著性差异，说明门控序列保留了原始序列中管腔面积和血管面积的相关信息，符合临床诊断需要。并且，通过原始序列和门控序列的血管横截面积方差、管腔横截面积的方差进行右边检验得出：门控序列的血管面积方差和管腔面积方差小于原始序列，即门控序列的管腔面积及血管面积变化比原始序列小，表明门控序列比原始序列稳定。

表 1(Table 1)

表 1 13组IVUS图像原始序列及关键帧门控序列的血管参数和分析统计 Table 1 Vascular parameters and statistic analysis on 13 IVUS non-gated versus key-frames gated sequences No Segment length (frames) Vessel volume (mm3) Lumen volume (mm3) Mean plaque burden (%) Variance test of vessel area Variance test of lumen area Original Gated Original Gated Original Gated No.1 891 175.87 174.41 146.56 143.95 16.66 17.46 H0 H0 No.2 883 268.37 265.63 239.08 236.50 10.91 10.97 H0 H0 No.3 916 131.89 123.62 118.41 109.80 10.22 11.18 H0 H0 No.4 711 194.96 191.71 94.83 94.82 51.36 50.54 H0 H0 No.5 912 107.28 103.93 50.61 48.85 52.82 53.00 H0 H0 No.6 873 430.72 427.64 270.01 264.92 37.31 38.05 H0 H0 No.7 915 133.97 129.66 94.10 90.67 29.76 30.07 H0 H0 No.8 893 121.52 119.88 103.69 102.18 14.68 14.77 H0 H0 No.9 785 120.41 119.45 81.82 81.25 32.05 31.98 H0 H0 No.10 933 196.49 191.98 117.21 117.86 40.35 38.61 H0 H0 No.11 890 303.50 296.11 273.27 267.41 9.96 9.69 H0 H0 No.12 921 256.41 246.32 215.28 206.88 16.04 16.01 H0 H0 No.13 748 107.29 103.83 52.89 51.94 50.70 49.98 H0 H0 Significant difference test 0.001 0.003 NS The confidence level of all hypothesis test is 0.05. NS indicates no significant difference between the original and the gated sequences. H0 represents a greater variance of the vessel cross-sectional area or the variance of the lumen cross-sectional area of the original sequence than the gated ones, while H1 indicates the opposite conclusion.

表 1 13组IVUS图像原始序列及关键帧门控序列的血管参数和分析统计 Table 1 Vascular parameters and statistic analysis on 13 IVUS non-gated versus key-frames gated sequences

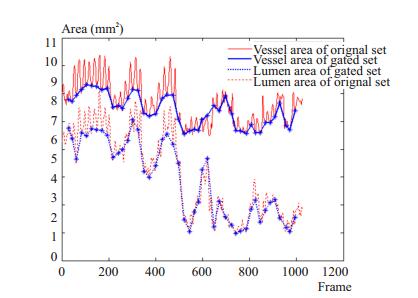
图 5为一组含有斑块的IVUS序列（No.7）及其门控序列的血管面积，管腔面积变化曲线。红色实线为原始序列血管面积变化曲线，红色虚线为原始序列管腔面积变化曲线，蓝色实线为门控序列血管面积变化曲线，蓝色虚线为门控序列管腔面积变化曲线，蓝色星号对应关键帧血管、管腔面积。门控序列面积变比原始序列平缓，保留了原始序列中的信息，具有更加直观的视觉效果。

综上所述，本文方法提取到的关键帧组成的门控序列的血管容积、管腔容积显著小于原始序列，门控前后序列的平均斑块负荷差异性不显著，满足临床诊断要求。门控序列的血管面积方差和管腔面积的方差显著小于原始序列，表明门控序列较原始序列稳定。

图 5(Figure 5)

图 5 原始序列和关键帧门控序列血管及管腔面积变化曲线 Figure 5 Vessel and lumen cross-sectional area of an original and key-frames gated set.

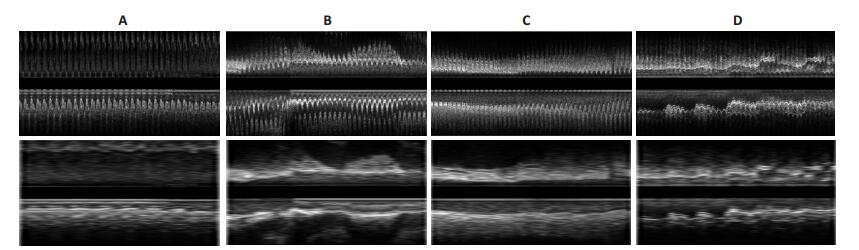
图 6为一组IVUS序列在不同的纵切方向上（0°，45°，90°，145°）的纵切图，上部为原始序列，下部为门控序列。图 7为四组序列关键帧检索的结果，上部为原始序列，下部为门控序列。从纵切图上观察到：由关键帧所组成的门控序列的管壁、管腔、斑块与原始序列具有高度的相似性，血管内腔和管壁轮廓和斑块比原始序列要平滑，连续性更好，抑制了锯齿状振荡，具有更好的视觉效果。

图 7(Figure 7)

图 7 4组IVUS原始序列及其门控序列的纵切图 Figure 7 Four original IVUS sequences and their longitudinal cuts and gated cuts.

文献[6]提出一种基于IVUS图像序列灰度的门控方法，其3个步骤为：（1）选择每帧图像像素点局部均值为参考点，沿序列形成一维信号簇，通过幅值滤波和光流滤波保留与心脏运动信息相关性很强的一维信号簇；（2）带通滤波一维信号簇，组成一个心动周期剖面图；（3）寻找滤波后的一维信号簇极值，提取关键帧。该方法能快速准确的提取门控序列。本文方法与文献[6]所提出的方法进行比较，N为实验序列长度，分别统计了两种方法得到的门控序列中关键帧帧数（N_p、N^_[6]），关键帧平均距离E_seq^[6]，以及关键帧之间的距离占心脏周期的比例分数E_seq^[6]，结果见表 2，可见两种方法得到的门控序列中的总帧数接近，E_seq，EF_seq值较小，说明两种方法检索到的关键帧比较一致。但文献[6]中方法对带通滤波器参数敏感，难以提取心率不齐患者及冠脉血管结构多变的IVUS图像序列的门控帧。

表 2(Table 2)

表 2 13本文方法与文献[6]方法对比结果 Table 2 Comparative results of our method and the method proposed in reference[6] No N N[6] Np Eseq(frames) EFseq(%) No.1 958 28 28 1.50±1.17 4.52±3.45 No.2 984 29 29 2.45±1.83 7.75±5.83 No.3 1006 42 42 0.86±0.57 3.86±2.57 No.4 1255 58 58 1.72±1.42 8.18±6.67 No.5 726 34 34 1.00±1.04 4.50±4.96 No.6 743 43 42 3.02±2.95 12.72±9.94 No.7 933 44 43 2.23±1.93 9.15±7.62 No.8 995 42 42 0.93±1.05 4.48±5.05 No.9 845 40 40 0.38±0.54 1.82±2.62 No.10 839 31 31 0.58±1.09 7.97±3.70 No.11 945 33 33 0.58±0.61 2.04±2.20 No.12 912 44 43 3.45±1.38 4.52±3.52 No.13 748 35 35 1.14±1.12 7.75±5.29

表 2 13本文方法与文献[6]方法对比结果 Table 2 Comparative results of our method and the method proposed in reference[6]

因为门控序列包含了原始序列中的关键信息，提取关键帧门控序列，降低了临床血管数据的分析量，相比于原始序列，门控序列具有更好的视觉效果。本文提出了一种简单的、稳定的基于IVUS图像序列的门控方法。应用流形学习的方法，将高维的IVUS数据降到低维流形中，减少了计算机存储和分析量。以低维流形中的特征分量作为显著性特征，构造距离函数，检索并提取心脏舒张末期的IVUS图像，组成关键帧门控序列。本文算法的优势体现为两方面：（1）存储和计算量减少；（2）对于心率不齐的患者，能准确地寻找门控序列。流形学习中的特征分量含有复杂的运动规律，如图像局部平移、旋转、尺寸变化等运动参数，本文仅针对IVUS图像序列纵向运动伪影的抑制进行研究，对短轴旋转伪影的抑制和补偿有待进一步探讨。