2. 南方医科大学南方医院 PET中心,广东 广州 510515
2. Southern Medical University, School of Biomedical Engineering, Guangzhou 510515, China
PET成像中部分容积效应(partial volume effect, PVE)会使图像模糊,图像中组织活度衰减,病灶边界识别不清,从而影响临床诊断[1]。因此减轻部分容积效应对PET图像的影响,对提高PET在肿瘤诊断和指导治疗上的应用至关重要。当前,诸多方法相继被提出以实现PET图像部分容积效应校正(partial volume correction, PVC)。其中一类方法是引入MR/CT解剖先验对PET图像进行部分容积校正,如在图像重建或后重建过程,通过分割和配准解剖图像,引入解剖图像的边缘或者区域信息[2-3]。然而这些方法首先要对解剖图像进行精确分割,而解剖图像分割尚无绝对鲁棒的方法。此外,此类方法主要针对大脑区域,极大限制了此类方法的应用。
基于图像后重建的去卷积校正技术提供了另一类解决方法。去卷积方法只需考虑PET图像本身信息,方法实现简单易行,更重要的是可以针对全身区域进行部分容积校正,如Teo等[4]首先应用Van Cittert(VC)去卷积算法[5]在PET肿瘤图像进行部分容积校正。然而,去卷积过程会引起高水平噪声,故作者提出应用这种算法只是针对特定的感兴趣区域(regions of interest, ROIs),例如经过很好勾勒出的肿瘤区域。Tohka和Reihac[6]应用VC和Richardson-Lucy(RL)[7-8]去卷积算法进行脑PET图像的部分容积校正,结果表明这两种去卷积方法都会导致图像噪声的增加。为解决校正过程中噪声增加的问题,本文将正则化项引入到去卷积模型中。全变分(total variation, TV)[9]已广泛应用于图像处理领域,能够在保持图像边缘的同时取得良好去噪效果。针对PET部分容积效应图像活度衰减、边缘模糊特点和传统去卷积方法噪声增加问题,本研究将全变分方法与传统迭代去卷积方法二者有机结合,提出基于全变分正则化的VC和RL去卷积算法,并与中值先验正则化[10]和贝叶斯正则化[11]的去卷积方法比较。
1 方法一般而言,去卷积方法的通用框架是基于以下模型:
| $ O\left( x \right) = I\left( x \right) \otimes h\left( x \right) + N\left( x \right) $ | (1) |
式中,O是探测得到的图像,I是真实理想的图像,h代表着点扩散函数(point spread function, PSF),N为加性噪声,x为空间坐标,⊗是卷积操作。
1.1 经典去卷积方法 1.1.1 Van Cittert(VC)去卷积算法Van Cittert(VC)去卷积算法是从探测得到的退化图像O中迭代恢复真实理想的图像I,将(1)式改写成最小二乘形式为:
| $ {J_1} = \sum\limits_x {{{\left\| {O\left( x \right)-\left( {I \otimes h} \right)\left( x \right)} \right\|}^2}} $ | (2) |
运用梯度下降法求解得到:
| $ {\tilde I^{n + 1}}\left( x \right) = {\tilde I^n}\left( x \right) + \alpha \left( {O\left( x \right)-h\left( x \right) \otimes {{\tilde I}^n}\left( x \right)} \right) $ | (3) |
式中,α是收敛参数一般设为1,
Richardson和Lucy提出了RL去卷积算法,依据贝叶斯理论,由(1)式可以得到:
| $ p\left( {I\left| O \right.} \right) = p\left( {O\left| I \right.} \right) \cdot \frac{{p\left( I \right)}}{{p\left( O \right)}} $ | (4) |
其中p(I|O)是后验概率,p(O|I)是似然概率,p(I)是目标图像的先验概率,p(O)是常数。
在去卷积问题中,假设PET图像统计过程为泊松过程,故似然概率p(O|I)能写成:
| $ p\left( {O\left| I \right.} \right) = \prod\limits_x {\frac{{{{\left[{\left( {h \otimes I} \right)\left( x \right)} \right]}^{O\left( x \right)}}\exp \left( { -\left( {h \otimes I} \right)\left( x \right)} \right)}}{{O\left( x \right)!}}} $ | (5) |
求解(5)式可以得到需要最小化求解的代价函数:
| $ {j_2} = \sum\limits_x {\left[{\left( {h \otimes I} \right)\left( x \right)-O\left( x \right) \cdot \log \left( {h \otimes I} \right)\left( x \right)} \right]} $ | (6) |
通过(6)式最小化求解,可以得到RL算法的最终形式:
| $ {\tilde I^{n + 1}}\left( x \right) = {\tilde I^n}\left( x \right) \cdot \left[ {\left( {\frac{{O\left( x \right)}}{{h\left( x \right) \otimes {{\tilde I}^n}\left( x \right)}} \otimes h\left( { - x} \right)} \right)} \right] $ | (7) |
式中,h(-x)是h(x)的共轭,
VC和RL两种去卷积方法都能用于PET图像的部分容积校正,但缺点是会引起高水平的噪声。因此,为了减少校正过程中噪声的增加,需要在去卷积步骤中引入正则化项。
1.2 全变分正则化全变分(total variation, TV)去噪模型是一种应用很广的滤波方法,优点是在保持边缘信息同时具有良好的去噪效果,三维情况下的TV式为:
| $ TV\left( I \right) = \int {\left| {\nabla I} \right|dxdydz = \int {\sqrt {\frac{{\partial {I^2}}}{{\partial x}} + \frac{{\partial {I^2}}}{{\partial y}} + \frac{{\partial {I^2}}}{{\partial z}}} dxdydz} } $ | (8) |
其与经典去卷积算法结合的正则化形式分为两种。
第一种是与VC去卷积算法结合,在(2)式中引入TV正则化项,则变为:
| $ {J_{TVI}} = \sum {{{\left\| {O\left( x \right)-\left( {I \otimes h} \right)\left( x \right)} \right\|}^2} + {\lambda _{TV}}\sum\limits_x {\left| {\nabla I\left( x \right)} \right|} } $ | (9) |
运用梯度下降法求解,则(9)式的迭代求解式为:
| $ \begin{array}{l} {{\tilde I}^{n + 1}}\left( x \right) = {{\tilde I}^n}\left( x \right) + \alpha \left( {O\left( x \right)-h\left( x \right) \otimes {{\tilde I}^n}\left( x \right)} \right) + \\ \alpha {\lambda _{TV}}{\rm{div}}\left( {\frac{{\nabla {{\tilde I}^n}\left( x \right)}}{{\left| {\nabla {{\tilde I}^n}\left( x \right)} \right|}}} \right) \end{array} $ | (10) |
式中,λTV是正则化参数,α是收敛参数一般设为1,div代表的是散度算子,▽为梯度算子,其余与(3)式定义相同。
第二种是与RL去卷积算法结合,在(6)式中引入TV正则化项,则可以改写成:
| $ \begin{array}{l} {J_{TV2}} = \sum\limits_x {\left[{\left( {h \otimes I} \right)\left( x \right)-O\left( x \right) \cdot \log \left( {h \otimes I} \right)\left( x \right)} \right]} \\ + {\lambda _{TV}}\sum\limits_x {\left| {\nabla I\left( x \right)} \right|} \end{array} $ | (11) |
求解(11)式可以得到:
| $ \begin{array}{l} {{\tilde I}^n}\left( x \right) = \left( {\frac{{O\left( x \right)}}{{{{\tilde I}^n}\left( x \right) \otimes h\left( x \right)}} \otimes h\left( {-x} \right)} \right) \cdot \\ \frac{{{{\tilde I}^n}\left( x \right)}}{{1-{\lambda _{TV}}{\rm{div}}\left( {\frac{{\nabla {{\tilde I}^n}\left( x \right)}}{{\left| {\nabla {{\tilde I}^n}\left( x \right)} \right|}}} \right)}} \end{array} $ | (12) |
式中,各变量定义与(10)式相同。
1.3 中值先验正则化为了抑制去卷积迭代过程中噪声的增加,在RL去卷积框架下,Kirov提出将中值先验(median root prior, MRP)[12]应用于去卷积过程中,用来构建迟一步MRP算法:
| $ {{\tilde I}^{n + 1}}\left( {\vec r} \right) = \frac{{{{\tilde I}^{n + 1, dec}}\left( {\vec r} \right)}}{{1 + \beta \frac{{{{\tilde I}^n}\left( {\vec r} \right)-{M_R}}}{{{M_R}}}}} $ | (13) |
这里的
贝叶斯正则化去卷积方法在Naqa文章中指的是在求解(1)式过程中使用最大后验方法,引入自身图像作为先验,在贝叶斯框架下,得到贝叶斯去卷积迭代公式为:
| $ {\tilde I^{n + 1}}\left( x \right) = {\tilde I^n}\left( x \right) \cdot \exp \left[{\left( {\frac{{O\left( x \right)}}{{h\left( x \right) \otimes {{\tilde I}^n}\left( x \right)}}-1} \right) \otimes h\left( {-x} \right)} \right] $ | (14) |
式中,各变量定义与(7)式相同,公式中的指数项强制正向收敛,从而起到正则化作用。
1.5 数值解法对于三维数据的的
| $ \begin{array}{l} \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\rm{div}}\left( {\frac{{\nabla I\left( x \right)}}{{\left| {\nabla I\left( x \right)} \right|}}} \right)\\ \begin{array}{*{20}{l}} {\Delta _ - ^x\frac{{\Delta _ + ^x + {I_{ijk}}}}{{\sqrt {{{\left( {\Delta _ + ^x{I_{ijk}}} \right)}^2} + m{{\left( {\Delta _ + ^y{I_{ijk}},\Delta _ - ^y + {I_{ijk}}} \right)}^2} + m{{\left( {\Delta _ + ^z + {I_{ijk}},\Delta _ - ^z + {I_{ijk}}} \right)}^2}} }} + }\\ {\Delta _ - ^y\frac{{\Delta _ + ^y + {I_{ijk}}}}{{\sqrt {{{\left( {\Delta _ + ^y{I_{ijk}}} \right)}^2} + m{{\left( {\Delta _ + ^x{I_{ijk}},\Delta _ - ^x + {I_{ijk}}} \right)}^2} + m{{\left( {\Delta _ + ^z + {I_{ijk}},\Delta _ - ^z + {I_{ijk}}} \right)}^2}} }} + }\\ {\Delta _ - ^z\frac{{\Delta _ + ^y + {I_{ijk}}}}{{\sqrt {{{\left( {\Delta _ + ^z{I_{ijk}}} \right)}^2} + m{{\left( {\Delta _ + ^x{I_{ijk}},\Delta _ - ^x + {I_{ijk}}} \right)}^2} + m{{\left( {\Delta _ + ^y + {I_{ijk}},\Delta _ - ^y + {I_{ijk}}} \right)}^2}} }}} \end{array} \end{array} $ | (15) |
其中,i=1...Nx, j=1...Ny, k=1...Nz
| $ \begin{array}{l} \Delta _ \pm ^x{I_{ijk}} = h_x^{-1}\left( { \mp {I_{ijk}} \pm {I_{\left( {i \pm 1} \right)jk}}} \right), \\ \Delta _ \pm ^y{I_{ijk}} = h_y^{-1}\left( { \mp {I_{ijk}} \pm {I_{i\left( {j \pm 1} \right)k}}} \right), \Delta _ \pm ^z{I_{ijk}} = h_z^{-1}\left( { \mp {I_{ijk}} \pm {I_{ij\left( {k \pm 1} \right)}}} \right)\\ \;\;\;\;\;\;\;\;\;\;\;m\left( {a, b} \right) = \frac{{\sin a + \sin b}}{2}\min \left( {\left| a \right|, \left| b \right|} \right) \end{array} $ |
同时hx, hy, hz是指像素的维数,一般都取1,在边界点,我们定义以下关系:
| $ \begin{array}{l} {I_{0jk}} = {I_{1jk}}, {I_{\left( {{N_x} + 1} \right)jk}} = {I_{_{{N_x}jk}}}, \\ {I_{j0k}} = {I_{j1k}}, {I_{i\left( {{N_y} + 1} \right)k}} = {I_{_{{N_y}jk}}}, \\ {I_{jk0}} = {I_{jk1}}, {I_{ij\left( {{N_z} + 1} \right)}} = {I_{ij{N_z}}} \end{array} $ | (16) |
计算平台是Intel Core i5-2400 @ 3.10GHz四核处理器、4GB内存的PC机。Matlab版本为7.11.0.584(R2010b)。
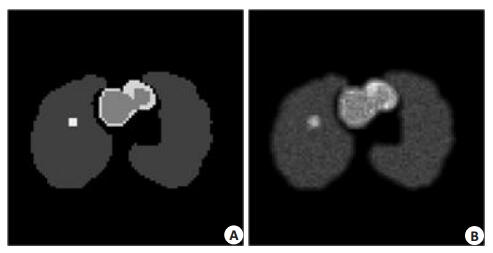
2 实验设计与评价 2.1 NCAT仿真实验本图 1A是大小为128 × 128的NCAT仿真PET图像,参数均来自文献[13]。图 1B是仿真存在部分容积效应和噪声的退化PET图像,退化图像的部分容积效应是在图像域中对体模图像进行半高宽为6 mm的高斯平滑,随后加入均值为0,方差为0.1的高斯噪声。
|
图 1 仿真NCAT图像 Figure 1 Simulated NCAT image. A: simulated PET image; B: degraded PET image with partial volume effect and noise. |
PET物理体模数据采用基于NEMA NU 4-2008标准的图像质量体模[14]。图 2为采用有机玻璃加工的体模,其圆柱长度为50 mm,直径为30 mm,包含直径为30 mm、高为30 mm的圆柱形空腔,还有高20 mm的固体部分。其中固体部分有5个直径依次为1、2、3、4、5 mm的可填充空腔棒,空腔棒与圆柱形空腔联通。

|
图 2 NEMA NU4-2008 IQ体模 Figure 2 NEMA NU4-2008 image-quality (IQ) phantom. |
我们在体模中注入21 ml活度浓度为174.8 kBq/ml的18F-FDG溶液,得到的总活度为3.67 MBq。在南方医院PET中心小动物Invoen micro PET上进行扫描。PET系统设置为默认设置,能量和事件符合时间分别为350~650 keV和3.432 ns。我们对体模进行20 min扫描,数据存储为list-mode格式,然后采用2D有序子集最大似然法(2D ordered subset expectation maximization, OSEM2D)重建图像(16个子集,4次迭代)。最终得到的三维图像数据是256 × 256 × 159,体素大小为0.39 × 0.39 × 0.79 mm。
2.3 肿瘤小鼠实验临床FDG数据是鼠源EMT6乳腺癌小鼠数据。我们使用南方医院Invoen microPET对注射18F-FDG总活度为12.95 MBq的肿瘤鼠进行10 min扫描,扫描过程机器的设置为默认设置。重建算法为OSEM2D,参数设置为16个子集,4次迭代。最终得到的三维图像数据是256 × 256 × 159,像素大小为0.39 × 0.39 × 0.79 mm。
2.4 定量评价指标针对部分容积效应校正后的图像,分别采用恢复系数(recovery coefficient, RC)和标准方差(standard deviation, SD)进行定量评价。
2.4.1 恢复系数恢复系数定义为:
| $ RC = \frac{{{X_{ROI}}}}{{X_{ROI}^{{\rm{tr}}ue}}} $ | (17) |
式中,XROI为探测图像感兴趣区域的活度值,XROItrue是真实图像感兴趣区域的活度值。
2.4.2 标准方差标准方差表示图像的噪声水平,定义如下:
| $ SD = \sqrt {\frac{1}{{N-1}}\sum\nolimits_j {{{\left( {{X_j}-\bar X} \right)}^2}} } \times 100\% $ | (18) |
式中,N是感兴趣区域的像素个数,Xj为感兴趣区域像素j(j=1, ..., N)处的像素值,X是感兴趣区域的均值。
同时,为了表示噪声的增加率,定义了标准方差的增加率:
| $ S{D_{increase}} = \frac{{S{D_{correct}}-S{D_{original}}}}{{S{D_{original}}}} \times 100\% $ | (19) |
式中,下标increase代表增加率,correct代表校正图像计算值,original代表校正前图像计算值。
2.4.3 参数优化针对重建得到的3D体模图像数据,记为Uncorrected data,分别用六种不同的方法进行部分容积校正。方法1是对图像数据进行VC去卷积,记为VC;方法2是对图像数据进行RL去卷积,记为RL;方法3是引入TV正则化项的VC去卷积,记为VC-TV;方法4是引入TV正则化项的RL去卷积,记为RL-TV;方法5是在RL框架下引入中值先验,记为MRP;方法6是对图像数据进行贝叶斯去卷积,记为Ba。在实验中,所有方法的迭代步数参数都为20。PSF作为影响算法校正结果的重要参数,本文选取半高宽(full width at half maximum, FWHM)参数为1.5 mm[15]。RL-TV和VC-TV的TV正则化参数为0.005;RL-MRP的滤波核大小设为3 × 3 × 3,β的取值为0.3。
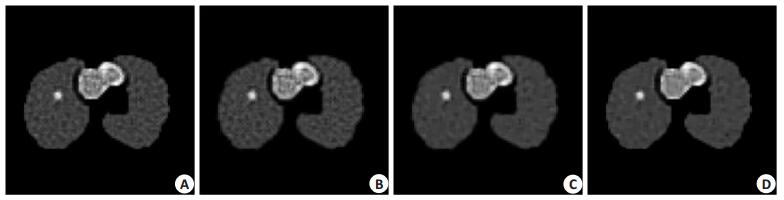
3 结果 3.1 仿真实验结果图 3是传统RL和VC去卷积算法和引入TV正则化项去卷积算法的结果。从图 3A和图 3B可以看出RL和VC都具有校正效果,但噪声水平高于校正前图像。而图 3C、D是RL-TV和VC-TV结果,可以看出在保持图像边缘信息的同时抑制了图像噪声的增加,达到很好的校正效果,其中RL-TV校正效果好于VC-TV。
|
图 3 NCAT仿真图像校正结果 Figure 3 Simulated NCAT image results. A: RL; B: VC; C: RL-TV; D: VC-TV. |
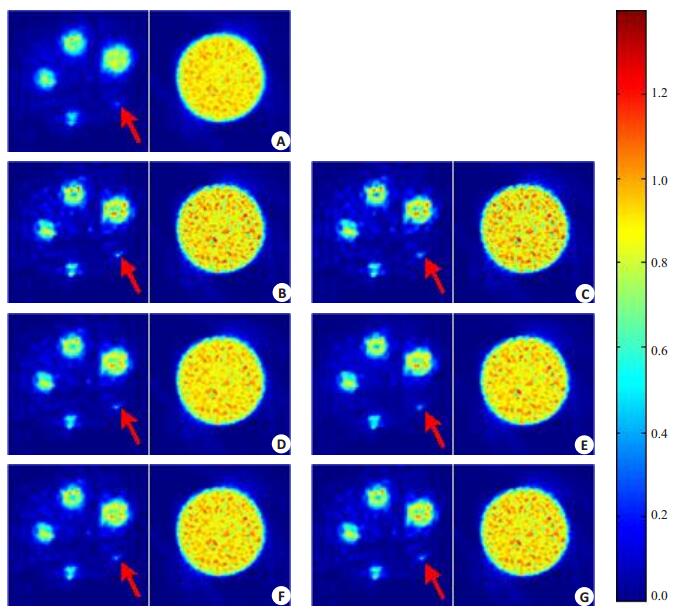
图 4给出了优化参数下不同方法对体模图像校正后的结果,所有图像均在同一显示窗下显示。图 4中各个图像的红色箭头均是指向最小直径(1 mm)的ROI(记为ROI 1)。由图 4A中可以看出在未校正图像的ROI 1在图像中亮度值很低,经过不同方法校正后可以看出ROI 1处亮度值都有提升。同时,5个ROI的图像是用RC来定量分析,空腔圆形图像是用来定量SD。
|
图 4 不同去卷积方法校正的体模图像 Figure 4 Various phantom images with different PVC algorithm.s The red arrow points to the smallest ROI (1 mm).A: Uncorrected data; B: RL; C: VC; D: RL-TV; E: VC-TV; F: Ba; G: MRP |
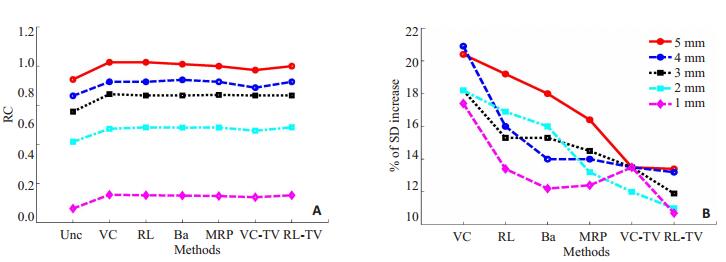
图 5描绘了优化参数后的不同去卷积方法在不同直径圆形感兴趣区域的RC和SD增加率变化曲线。从图 5A可以看出,直径越大的圆形感兴趣区域的RC值越接近于1,同时校正后的RC值的增加率范围为9.7%±2.2%(ROI 5)到(25.9±1.2)%(ROI 1)。图 5B展示了不同校正方法的SD增加率曲线,即噪声增加水平。首先,感兴趣区域的直径大小与校正后引入的噪声有较大联系,基本上是直径越大,引入噪声越多,但在ROI 2处的RL和Ba方法引入噪声反而较在ROI 3和ROI 4处多。其次,针对不同的去卷积算法,VC的SD增加率最大,范围是从17.4%到20.9%。RL较VC表现更好,噪声引入较少,但仍然保持较高水平。另一方面,图 5B中不同的正则化方法都能在一定程度抑制噪声的增加。其中在ROI2-ROI5条件下,MRP优于Ba,TV正则化算法优于MRP和Ba,而且RL-TV要优于VC-TV。特别地在ROI1处,Ba优于MRP和VC-TV。RL-TV在RC相等情况下,噪声抑制效果最好,SD增加率的范围为10.7%~13.4%。
|
图 5 不同去卷积方法在不同直径感兴趣区域的RC和SD增加率变化曲线 Figure 5 Plots of RC and SD increase percentage using different methods varying ROIs. A is for RC; B is for SD increase percentage. |
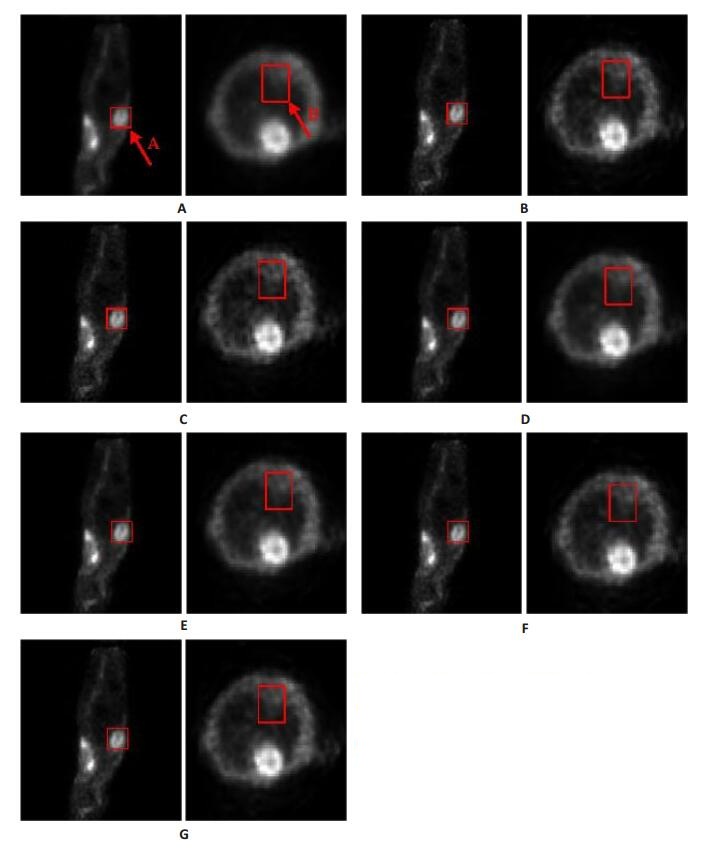
图 6是不同去卷积方法对小鼠数据校正结果,所有图像都在同一灰度窗下显示。图 6A中ROI A所在图像为矢状面图(以下相同),ROI A为肿瘤区域,ROI B所在图像为横切面图(以下相同),ROI B用来测量噪声的增加。实验中,我们保证各个去卷积校正方法对肿瘤区域即ROI A有近似一致的活度增强效果取(10±1.8)%增加率),从而考虑ROI B中噪声增加情况。表 1给出了不同去卷积方法对小鼠数据校正后具体活度增加率和SD增加率的数值比较,易见,RL-TV算法在肿瘤活度增加率最大的条件下,噪声增加率最小。
|
图 6 不同去卷积方法校正的小鼠图像 Figure 6 Corrected mouse tumor images with different algorithms. ROI A: sagittal view (tumor); ROI B: transverse view. A: Uncorrected image; B: RL; C: VC; D: RL-TV; E: VC-TV; F: Ba; G: MRP. |
| 表 1 小鼠图像校正后活度和SD增加率比较 Table 1 Comparison of intensity and SD increase percentage for mouse images |
最初是在1979年,Hoffman等[16]提出用恢复系数来描述并校正部分容积效应。该法主要是测量标准质量体模的不同直径区域的恢复系数,但是临床图像的病灶区域形状是不规则的,体模实验确定的恢复系数难以用于临床。随后有学者将迭代去卷积算法应用于PET肿瘤图像的部分容积校正。Kirov等人提出的基于RL去卷积方法的MRP算法能够有效校正图像同时抑制噪声,但是在考虑拓扑结构时需手动调节的参数有9个,本文只是讨论了其中最重要的一个参数β。而本文方法,总共只有两个参数,大大减少了人为因素的影响。Boussion等[17]提出在去卷积过程中引入小波滤波,但3D情况下只能对每层图像单独处理后加和,不能实现纯粹意义上的3D处理,因此本文不将此方法作为比较。Naqa等人提出Bayesian正则化去卷积方法,这种方法只是对传统RL方法在形式上做了修改,引入了指数项的正向收敛,在NU4 2008体模实验和肿瘤小鼠实验中都表明此方法不能有效去除噪声。
本研究在经典去卷积方法的基础上,引入全变分正则化项,在仿真体模实验结果图 3中视觉显示该法可以在保持图像边缘的同时有效抑制噪声的增加。定量实验中,全变分正则化项方法在校正效果相同(具有相同的RC值或者一致的活度增加率),相比于其他校正方法,具有最低的噪声增加率,其中RL-TV优于VC-TV,表明了本文提出方法的优越性。在本文的实验过程中,λ的选择是根据量化准则优化选取,然而如何在临床应用中建立相应的优化参数选择,是本文进一步需要开展的研究。基于此,我们将采用临床半定量,如标准吸收值或定量的指标,提出自适应的参数选择算法,更好的服务于临床。
综上所述,本文提出了一种基于全变分正则化去卷积的PET图像部分容积校正方法。针对传统RL和VC迭代去卷积方法引起的噪声增加问题,本文提出的TV正则化去卷积方法在仿真实验、物理体模实验、肿瘤小鼠实验中都展示了抑制噪声增加, 保持图像边缘的优越性,尤其是RL-TV方法在文章中提到的方法中具有最好的去噪效果。
| [1] | 耿建华, 陈盛祖, 陈英茂, 等. 正电子图像部分容积效应成因与校正的理论探讨[J]. 中华核医学杂志,2003, 23 (5) : 318-9. |
| [2] | Lu LJ, Ma JH, Huang J, et al. Generalized metrics induced anatomical prior for MAP PET image Reconstruction[C]// Potsdam (Germany), 2011: 233-6. |
| [3] | Müller-Gärtner HW, Links JM, Prince JL, et al. Measurement of radiotracer concentration in brain gray matter using positron emission tomography: MRI-based correction for partial volume effects[J]. J Cereb Blood Flow Metab,1992, 12 (4) : 571-83. DOI: 10.1038/jcbfm.1992.81. |
| [4] | Teo BK, Seo Y, Bacharach SL, et al. Partial-volume correction in PET: validation of an iterative postreconstruction method with phantom and patient data[J]. J Nucl Med,2007, 48 (5) : 802-10. |
| [5] | Van CP. ZumEinfluß der spaltbreite auf die intensit?tsverteilung in spektrallinien[J]. ZeitschriftfürPhysik,1930, 65 (7/8) : 547-63. |
| [6] | Tohka J, Reilhac A. Deconvolution-based partial volume correction in Raclopride-PET and Monte Carlo comparison to MR-based method[J]. Neuroimage,2008, 39 (4) : 1570-84. DOI: 10.1016/j.neuroimage.2007.10.038. |
| [7] | Richardson WH. Bayesian-based iterative method of image restoration[J]. JOSA,1972, 62 (1) : 55-9. DOI: 10.1364/JOSA.62.000055. |
| [8] | Lucy LB. Iterative technique for rectification of observed distributions[J]. Astron J,1974, 79 (6) : 745-54. |
| [9] | Rudin LI, Osher S, Fatemi E. Nonlinear total variation based noise removal algorithms[J]. Physica D,1992, 60 (1/4) : 259-68. |
| [10] | Kirov AS, Piao JZ, Schmidtlein CR. Partial volume effect correction in PET using regularized iterative deconvolution with variance control based on local topology[J]. Phys Med Biol,2008, 53 (10) : 2577-91. DOI: 10.1088/0031-9155/53/10/009. |
| [11] | El Naqa I, Low DA, Bradley JD, et al. Deblurring of breathing motion artifacts in thoracic PET images by deconvolution methods[J]. Med Phys,2006, 33 (10) : 3587-600. DOI: 10.1118/1.2336500. |
| [12] | Alenius S, Ruotsalainen U. Bayesian image Reconstruction for emission tomography based on median root prior[J]. Eur J Nucl Med,1997, 24 (3) : 258-65. |
| [13] | Karakatsanis NA, Lodge MA, Tahari AK, et al. Dynamic whole-body PET parametric imaging: I. Concept, acquisition protocol optimization and clinical application[J]. Phys Med Biol,2013, 58 (20) : 7391-418. DOI: 10.1088/0031-9155/58/20/7391. |
| [14] | NEMA, NU 4-2008. National electrical manufacturers association[S]: nema standards publication, 2008. |
| [15] | Visser EP, Disselhorst JA, Brom MA, et al. Spatial resolution and sensitivity of the inveon Small-Animal PET scanner[J]. Journal of Nuclear Medicine,2009, 50 (1) : 139-47. |
| [16] | Hoffman EJ, Huang SC, Phelps ME. Quantitation in positron emission computed tomography: 1. Effect of object size[J]. J Comput Assist Tomogr,1979, 3 (3) : 299-308. DOI: 10.1097/00004728-197906000-00001. |
| [17] | Boussion N, Cheze Le Rest C, Hatt M, et al. Incorporation of wavelet-based denoising in iterative deconvolution for partial volume correction in whole-body PET imaging[J]. Eur J Nucl Med Mol Imaging,2009, 36 (7) : 1064-75. DOI: 10.1007/s00259-009-1065-5. |
 2015, Vol. 35
2015, Vol. 35
