临床X射线CT检查中的高剂量X射线照射会引发白血病、癌症和其他多种遗传性疾病[1]。如何在不影响临床诊断信息的条件下,最大限度地降低CT放射剂量已成为近年来CT领域亟待解决的关键性课题。当前,诸多策略相继被提出以实现低剂量CT成像[2-3],其中降低管电流和(或者)减少曝光时间(mAs)是最为简单的操作方法[4]。然而,该方法虽可以一定程度上降低辐射剂量,但是将导致相应投影数据中的量子噪声急剧增加,表现为重建图像中的大量噪声和伪影[5]。针对此问题,迭代重建方法(iterative reconstruction, IR)被引入至CT图像重建中,以实现优质的低剂量成像[6]。
为了有效地消除噪声并保持图像的结构和边缘信息,IR图像重建模型中需要引入先验信息加以约束,数学上此约束亦称为正则化(也称为惩罚函数)。通常,正则化多设计成一个二次惩罚函数,来惩罚图像某一局部区域中不同像素点间的灰度差值,其效果是噪声得到抑制而部分边缘细节也会丢失[8]。为了克服二次函数的上述缺点,多种边缘保持正则化被提出[9],其中Huber正则化最具有代表性[10]。Huber正则化采用一个非二次的惩罚函数代替原来的二次惩罚函数,且满足凸性和对称性,使得它能在减少噪声的同时有效地保持图像边缘信息。然而,Huber正则化的一个主要缺点是阈值需要依据具体重建目标人工选定,大大限制了其更为广泛的实际应用。针对此问题,许多文献讨论了Huber正则化阈值选取方法[11-15]。例如,Yang等[12]在Huber函数中引入了另一个阈值以便区分图像的边缘与伪影;Rousseeuw等[13]利用鲁棒性统计方法来检测奇异值,再利用全局边缘检测算子实现阈值选择;Black和Sapio [14]利用图像的局部统计特性,提出了用局部边缘检测算子进行阈值选择;He等[15]定义了一个比例因子,用拉普拉斯卷积核作为离散平滑算子对阈值进行限制。鉴于上述,本文重点研究基于全局和局部边缘检测算子的两种不同的Huber正则化阈值自适应选取方法,并将其应用于基于投影数据统计特征的惩罚加权最小二乘(penalizedweighted least squares,PWLS)低剂量CT图像迭代重建中,其算法性能通过数值仿真进行验证。
1 方法 1.1 惩罚加权最小二乘CT重建算法在不考虑散射噪声的情况下,CT的测量可以表示为一个离散的线性系统:
| $ y = H\mu $ | (1) |
式中,μ=(μ1, μ2, ..., μn)T为待重建图像的衰减系数。y=(y1, y2, ...yM)T表示测量得到的弦图数据(经过系统校正和对数变换之后的投影数据),其中‘T’代表矩阵的转置,H表示大小为M×N的系统矩阵,元素Hi, j代表像素j对投影射线i的权值。CT图像重建的目的是从测量数据y中估计出衰减系数μ。
根据CT的测量模型(1)和最大后验(maximum aposteriori,MAP)估计方法,带有正则化项R(μ)的PWLS图像重建能量方程可表示为:
| $ \mu * = \mathop {arg\lim }\limits_{\mu \ge 0} \left\{ {\left( {y - H\mu } \right)'\sum {^{ - 1}\left( {y - H\mu } \right) + \beta R\left( \mu \right)} } \right\} $ | (2) |
其中,∑表示元素为δi2对角矩阵,δi2为弦图数据yi的方差,β为一个用来控制正则化强度的超参数。
我们可以利用多种方法[8, 16]来确定公式(2)中的参数δi2,在本文中,我们使用Ma等[16]提出的均值方差理论:
| $ \delta _i^2 = \frac{1}{{{I_0}}}\exp \left( {{{\bar p}_i}} \right)\left( {1 + \frac{1}{{{I_0}}}\exp \left( {\delta _e^2 - 1.25} \right)} \right) $ | (3) |
式中I0为入射X线强度,p i为在像素i处弦图数据的均值,δe2为背景电子噪声的方差。
1.2 Huber正则化传统上,式(2)中的正则化项R(μ)通过对图像中相邻像素间灰度的差值进行加权求和计算求得[8],可以描述为如下形式:
| $ R\left( \mu \right) = \sum\limits_j {R\left( \mu \right)} = \sum\limits_j {\sum\limits_{k \in {S_j}} {\omega \left( {k,j} \right)\varphi \left( {{\mu _j} - {\mu _k}} \right)} } $ | (4) |
式中j为图像域中所有像素的索引,Sj表示二维空间第j个像素点的邻域。权重ω(k, j)表示像素k和像素j相互关系的正常数,为正值并且是对称的,即ω(k, j)≥0且ω(k, j)=ω(j, k)。ω(k, j)通常被设定为邻域Sj内像素k和j之间距离的反比。φ表示一个凸的正势函数并且满足φ(0)=0。φ(t)的选择方法有许多种,本文使用Huber正则化φHuber,其定义为:
| $ {\varphi _{Huber}}\left( t \right) = \left\{ {\begin{array}{*{20}{l}} {{t^2}/2,\;\;\;\;\;\;\;\;\;\;\left| t \right| \le \delta }\\ {\delta \left| t \right| - {\delta ^2}/2,\;\;\left| t \right| > \delta } \end{array}} \right. $ | (5) |
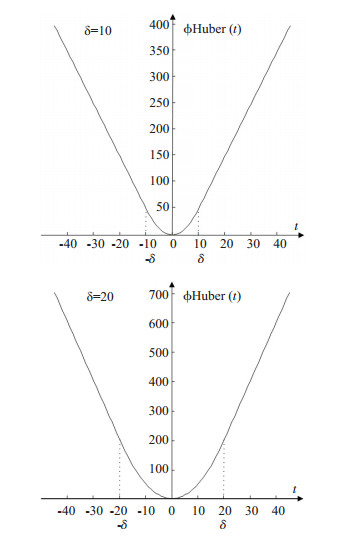
如图 1所示,Huber正则化为一个凸函数,且满足对称性,它可以根据图像当前像素点与其邻域内其他像素点间的灰度差值来调整对不连续区域的惩罚,这一作用由其阈值δ实现。阈值δ把Huber正则化分为3个部分,当图像梯度满足|t|≤δ时,正则化的二次项部分对图像连续区域进行较重的惩罚;当梯度|t| > δ时,正则化的线性部分对图像进行较轻的惩罚来保持图像的锐利特性,比如图像的边缘。
|
图 1 Huber正则化 Figure 1 Example of Huber regularization with different thresholds. |
综上所述,在CT图像重建中带有Huber正则化的PWLS算法(PWLS-Huber)的目标函数可以写成以下形式:
| $ \mu * = \mathop {arg\lim }\limits_{\mu \ge 0} \left\{ {\left( {y - H\mu } \right)'\sum {^{ - 1}\left( {y - H\mu } \right) + \beta {R_{Huber}}\left( \mu \right)} } \right\} $ | (6) |
其中Huber正则化项为:
| $ {R_{Huber}}\left( \mu \right) = \sum\limits_j {\sum\limits_{k \in {S_j}} {\omega \left( {k,j} \right){\varphi _{Huber}}\left( {{\mu _j} - {\mu _k}} \right)} } $ | (7) |
在实际运用中,我们用一种改进的共轭梯度法来优化此目标函数。
1.3 Huber正则化阈值选择方法Huber正则化的主要优点是它能根据图像当前像素点与其相邻像素点间的灰度差值来调节对不连续区域的惩罚,这一作用由其阈值δ实现。因此,对Huber函数来说选择一个合理的阈值是非常重要的。针对此问题,本文主要研究基于全局和局部边缘保持算子的Huber正则化阈值选取方法以及其在低剂量CT图像重建中的应用。
1.3.1 全局边缘检测方法各向异性扩散被视为一个稳健统计学过程,它能从含有噪声的数据中估算出分段平滑的图像,已经在图像边缘保持中得到了广泛应用。根据Perona和Malik[17]的传统公式,具有较大梯度幅值的像素点被视为奇异点,又被视为图像的边缘。这一解释可用来定义和检测图像分段平滑区域的边界。当一个像素点的梯度幅值小于阈值δ时,我们认为该像素点不属于奇异点;否则,该像素点属于奇异点。全局边缘检测方法的主要思想是阈值δ应该描述整幅图像数据的主要方差特性[13],即阈值应该描述图像中除边缘外其他像素点梯度的变化。根据这一思想,我们用稳健统计学方式计算出图像所有像素点梯度的方差,然后利用各向异性扩散方法确定空间变化的边缘阈值。因此,对于阈值δ的鲁棒性测量可通过如下方法:
| $ \begin{array}{*{20}{c}} {{\delta _G} = 1.4826MAD\left( {\nabla I} \right)}\\ { = 1.4826median\left( {\left\| {\nabla I - media{n_I}\left( {\nabla I} \right)} \right\|} \right)} \end{array} $ | (8) |
式中,MAD表示中位数绝对偏差。鉴于均值为0方差为1的标准正态分布的中位数绝对偏差是0.6745=1/1.4826,故将常数项设为1.4826。
1.3.2 局部边缘检测方法基于全局边缘检测算子的Huber正则化阈值对于整幅图像来说是相同的,然而我们也可以根据图像的局部统计特性来构造一个可变化的阈值:对平滑的区域,选择较大的阈值以提高去除噪声和伪影的能力;对纹理较重的区域,选择较小的阈值,以保持图像的边缘。局部边缘检测方法描述的是相对于局部图像而言怎样通过图像的梯度信息确定某一模块内的阈值δL(p, q)[14],其主要思想是δL(p, q)应该描述图像中某局部区域数据的方差特性。δL(p, q)在整个图像数据中是变化的,某一点是否属于图像边缘由局部图像梯度的变化特性决定。
局部边缘检测方法和全局边缘检测方法有相同的稳健统计学理论基础。特别地,我们考虑在图像的一个大小为n×n的模块内(这里的模块是一个图像像素的空间位置函数,这种模块覆盖整个图像),计算其对应的局部阈值δL(p, q),公式可以写为:
| $ {\delta _L}\left( {p,q} \right) = 1.4826MA{D_{ - \frac{n}{2} < i,j < \frac{n}{2}}}\left( {\nabla {I_{p + i,q + j}}} \right) $ | (9) |
本文使用XCAT体模[18]生成仿真CT投影数据,并用上述两种方法对该投影数据分别进行重建。实验中,标准剂量数据剂量为580 mAs,低剂量为23.2 mAs。投影数据采用文献[16]中所述方法生成,其中,仿真CT扫描的成像参数如下:管电压为120 kVp,旋转1周采样值为1160;探测器单元的个数为672,大小为0.8448 mm;X射线源到探测器和旋转中心的距离分别为1361 mm和746 mm;体模大小为512×512;层厚为3 mm。实验平台为Intel(R)Pentium(R)CPU G620 @ 2.60 GHz四核处理器,3GB内存的PC机,程序采用Matlab实现。基于本文研究的两类Huber正则化阈值自适应选取方法的PWLS-Huber算法迭代设定为50次,耗时大约为40 min。
本文采用以下两种图像质量测度来评价重建图像质量:局部信噪比(local signal-to-noise ratio, lSNR)和相对均方根误差(relative root mean square error, rRMSE),其计算公式分别如下:
| $ lSNR = \frac{{\frac{1}{Q}\sum\limits_{m = 1}^Q {{\mu _m}} }}{{\sqrt {\frac{1}{Q}\sum\limits_{m = 1}^Q {{{\left( {{\mu _m} - \frac{1}{Q}\sum\limits_{m = 1}^Q {{\mu _m}} } \right)}^2}} } }} $ | (10) |
| $ rRMSE = \sqrt {\frac{{\sum\limits_{m = 1}^Q {{{\left| {{\mu _m} - {\mu _{G,m}}} \right|}^2}} }}{{\sum\limits_{m = 1}^Q {{{\left| {{\mu _{G,m}}} \right|}^2}} }}} $ | (11) |
μ表示低剂量投影数据重建出的图像,μG表示标准图像,m是感兴趣区域(Region of Interest, ROI)内像素的索引,Q是ROI内像素点的数量。在实验中,标准图像由在120 kVp、580 mAs条件下获得的投影数据采用基于hann窗的FBP算法重建得到。
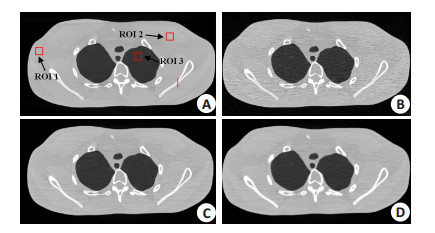
图 2显示了采用仿真数据重建得到的XCAT体模图像和低剂量CT图像。图 2A为标准剂量图像,结构清晰,几乎不含任何噪声和伪影,作为参照图像。图 2B为在23.2 mAs条件下(除标准图像外,其余图像的投影数据均在23.2 mAs条件下获得)获得的投影数据采用FBP重建得到的图像。和图 2A相比,图 2B中含有严重的噪声和伪影。图 2C为采用基于全局边缘检测算子的PWLS-Huber算法重建得到的图像。从图 2C可以看出图像中条形伪影明显减少,噪声水平大为降低,图像质量得到显著提高。图 2C为采用基于局部边缘检测算子的PWLS-Huber算法重建得到的图像。在图 2D中我们得到了与图 2C相似的结果。由此可以看出,这两种自适应Huber正则化阈值选择方法,均可得到比较理想的结果--大部分噪声和伪影得到了较好的抑制。进一步观察可以发现,虽然图 2C和2D中伪影均得到了较好的抑制,但是仍有部分伪影存在,图像边缘的锐利度在一定程度上降低。相比之下,图 2C对图像边缘保持的相对较好,看起来较为清晰;图 2D则对的噪声的抑制效果较好。
|
图 2 仿真投影数据重建出的XCAT体模图像和低剂量CT图像 Figure 2 XCAT phantom image and low-dose images reconstructed from the simulated projection data. A: Image reconstructed by the FBP method with optimal hanning filter from the projection data acquired with 580 mAs; B: Image reconstructed by the FBP method with ramp filter from the projection data acquired with 23.2 mAs; C: Image reconstructed by the PWLS-Huber algorithm with the global-edge-detecting operator from the projection data acquired with 23.2 mAs (β=1.0 × 103); D: Image reconstructed by the PWLS-Huber algorithm with the local-edge-detecting operator from the projection data acquired with 23.2 mAs (n=9 × 9, β=1.0 × 103). The display option is [0, 0.03]. |
为了定量分析这两种Huber正则化阈值选择方法的差异,我们计算了对应于图 2A中感兴趣区域的lSNR和rRMSE,结果如表 1所示。可以看出,相对于FBP重建图像,采用基于全局和局部边缘检测算子的PWLS-Huber算法重建得到的图像lSNR显著提高、rRMSE明显减小,具有更高的增益。此外,局部边缘检测算子在对连续区域的噪声抑制方面的表现优于全局边缘检测算子。
| 表 1 对应于图 2A中所示3个ROI的lSNR和rRMSE Table 1 LSNR and rRMSE measured on the ROIs as indicated by the squares in Fig.2A |
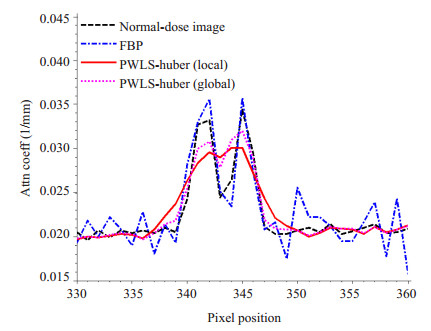
图 3中绘出了对应于图 2中各重建图像的垂直剖面线,鉴于剖面线中含有512个像素点,若全部显示则难以区分各重建方法,故仅截取其中一段(即图 2A中红色线段所示)显示,区间为[330, 360]。由图 3可以看出,在目标区域基于两种不同Huber正则化阈值选择方法的PWLS-Huber方法的重建值和标准值都较为接近,但局部边缘检测算子比全局边缘检测算子损失了更多的图像分辨率。
|
图 3 对应于图 2A中红色线段(x=408,y=[330, 360])的垂直剖面曲线 Figure 3 Vertical profiles located at the pixel position x=408 and y from 330 to 360 as indicated by the red line in Fig.2A. |
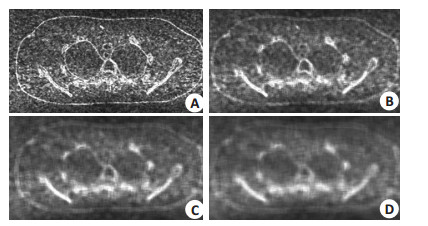
对于全局边缘检测方法,Huber正则化的阈值计算出来就固定不变了。但是,对于局部边缘检测方法,每个小模块内的阈值是不同的。为了证明模块大小对重建图像质量的影响,我们对局部边缘检测方法的做了进一步的实验。图 4展示了在不同模块大小情况下局部边缘检测方法对δL(p, q)的估计值。亮的区域对应图像中纹理重的区域,具有更高的δL(p, q)值。可以看出,当所选模块较小时,不连续区域中不同模块间阈值的差异比较明显;随着模块的增大,不同模块间阈值的差异也逐渐减小。图 5展示了在不同模块大小情况下,采用基于局部边缘检测算子的PWLS-Huber算法重建得到的图像。可以看出δL(p, q)大小变化对重建图像的质量影响不明显。为了进一步量化分析,表 2给出了对应图 5所示图像的不同ROI的lSNR和rRMSE。可以看出,模块大小从5×5到17×17变化的过程中重建图像的质量变化很小。当模块大小为9×9时,我们可以得到一幅质量相对较高的图像。
|
图 4 局部边缘检测方法对应的δL(p, q)值的估计,亮的区域对应较大的δL(p, q)值 Figure 4 Local estimate of scale δL(p, q). Bright areas correspond to larger values of δL(p, q). A: n=5×5; B: n=9×9; C: n=13×13; D: n=17×17. |
|
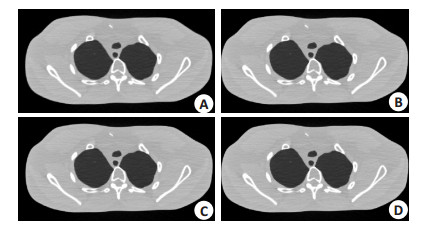
图 5 采用基于局部边缘检测算子的PWLS-Huber算法重建得到的图像 Figure 5 Images reconstructed by the PWLS-Huber algorithm with the local-edge-detecting method of different patch size. A: n=5×5; B: n=9×9; C: n=13×13; D: n=17×17. The display option is [0, 0.03]. |
| 表 2 对应图 5所示图像不同ROI的lSNR和rRMSE Table 2 LSNR and rRMSE measures on the ROIs in Fig.5 with different local patch size |
针对Huber正则化的阈值需要依据具体重建目标人工选定的问题,本文主要研究了基于全局和局部边缘保持算子的Huber正则化阈值选取方法以及其在低剂量CT图像重建中的应用,并且对他们做了定性和定量的测量与分析。实验结果表明局部边缘检测方法在对连续区域的噪声抑制方面的表现优于全局边缘检测方法。这可能是由于由噪声引起的条形伪影区域和高衰减区域的δL(p, q)值相对较大。但另一方面,从图像过度平滑的边缘可以看出,局部边缘检测方法比全局边缘检测方法牺牲了更多的图像分辨率。综上所述,这两种基于稳健统计学的Huber正则化阈值选取方法对噪声和伪影的抑制效果较好,各有优点,在使用时,可以根据对重建图像质量的具体要求加以选择。
| [1] | Brenner DJ, Hall EJ. Computed tomography--an increasing source of radiation exposure[J]. N Engl J Med,2007, 357 (22) : 2277-84. DOI: 10.1056/NEJMra072149. |
| [2] | Yu L, Liu X, Leng S, et al. Radiation dose reduction in computed tomography: techniques and future perspective[J]. Imaging Med,2009, 1 (1) : 65-84. DOI: 10.2217/iim.09.5. |
| [3] | Kalender WA, Wolf H, Suess C, et al. Dose reduction in CT by on-line tube current control: principles and validation on phantoms and cadavers[J]. Eur Radiol,1999, 9 (2) : 323-8. DOI: 10.1007/s003300050674. |
| [4] | Yazdi M, Beaulieu L. Artifacts in spiral x-ray CT scanners:problems and solutions[J]. Int J Biol Med Sci,2009, 4 (3) : 135-9. |
| [5] | Li TF, Xiang L, Jing W, et al. Nonlinear sinogram smoothing for low-dose X-ray CT[J]. IEEE Trans Nuclear Sci,2004, 51 (5) : 2505-13. DOI: 10.1109/TNS.2004.834824. |
| [6] | Elbakri IA, Fessler JA. Statistical image Reconstruction for polyenergetic X-ray computed tomography[J]. IEEE Trans Med Imaging,2002, 21 (2) : 89-99. DOI: 10.1109/42.993128. |
| [7] | Wang J, Li T, Xing L. Iterative image Reconstruction for CBCT using edge-preserving prior[J]. Med Phys,2009, 36 (1) : 252-60. DOI: 10.1118/1.3036112. |
| [8] | Wang J, Li T, Lu H, et al. Penalized weighted least-squares approach to sinogram noise reduction and image Reconstruction for low-dose X-ray computed tomography[J]. IEEE Trans Med Imaging,2006, 25 (10) : 1272-83. DOI: 10.1109/TMI.2006.882141. |
| [9] | Yu DF, Fessler JA. Edge-preserving tomographic Reconstruction with nonlocal regularization[J]. IEEE Trans Med Imaging,2002, 21 (2) : 159-73. DOI: 10.1109/42.993134. |
| [10] | Shulman D, Herve JY. Regularization of discontinuous flow fields[C]. Proc Workshop on Visual Motion, 1989: 81-86. |
| [11] | Shi M, Yi Q, Gong J. A New deblocking algorithm based on wavelet transform and MRF for DCT-coded images[C]. Conference on Electricaland Computer Engineering, 2006. |
| [12] | Yang J, Wu H. An improved Huber-MAP post filtering method.International Symposium on Communications[C]. Control and Signal Processing, 2008. |
| [13] | Rousseeuw PJ, Leroy AM. Robust regression and outlier detection[M]. New York: Wiley, 1987 . |
| [14] | Black MJ, Sapiro G. Edges as outliers: anisotropic smoothing using local image statistics[C]. Proc Scale-Space Theories in Computer Vision, 1999: 259-70. |
| [15] | Hu H, Kondi LP. Choice of threshold of the Huber-Markov prior in MAP-based video resolution enhancement[C]. Conference on Electrical and Computer Engineering, 2004. |
| [16] | Ma JH, Liang ZR, Fan Y, et al. Variance analysis of x-ray CT sinograms in the presence of electronic noise background[J]. Med Phys,2012, 39 (7) : 4051-65. DOI: 10.1118/1.4722751. |
| [17] | Perona P, Malik J. Scale-space and edge detection using anisotropic diffusion[J]. IEEE Trans Pattern Ana Mach Intell,1990, 12 (7) : 629-39. DOI: 10.1109/34.56205. |
| [18] | Segars WP, Sturgeon G, Mendonca S, et al. 4D XCAT phantom for multimodality imaging research[J]. Med Phys,2010, 37 (9) : 4902-15. DOI: 10.1118/1.3480985. |
 2015, Vol. 35
2015, Vol. 35
