A dual-domain cone beam computed tomography reconstruction framework with improved differentiable domain transform for cone-angle artifact correction

doi:10.12122/j.issn.1673-4254.2024.06.21

Abstract

Abstract:

Objective We propose a dual-domain cone beam computed tomography (CBCT) reconstruction framework DualCBR-Net based on improved differentiable domain transform for cone-angle artifact correction. Methods The proposed CBCT dual-domain reconstruction framework DualCBR-Net consists of 3 individual modules: projection preprocessing, differentiable domain transform, and image post-processing. The projection preprocessing module first extends the original projection data in the row direction to ensure full coverage of the scanned object by X-ray. The differentiable domain transform introduces the FDK reconstruction and forward projection operators to complete the forward and gradient backpropagation processes, where the geometric parameters correspond to the extended data dimension to provide crucial prior information in the forward pass of the network and ensure the accuracy in the gradient backpropagation, thus enabling precise learning of cone-beam region data. The image post-processing module further fine-tunes the domain-transformed image to remove residual artifacts and noises. Results The results of validation experiments conducted on Mayo's public chest dataset showed that the proposed DualCBR-Net framework was superior to other comparison methods in terms of artifact removal and structural detail preservation. Compared with the latest methods, the DualCBR-Net framework improved the PSNR and SSIM by 0.6479 and 0.0074, respectively. Conclusion The proposed DualCBR-Net framework for cone-angle artifact correction allows effective joint training of the CBCT dual-domain network and is especially effective for large cone-angle region.

Key words: cone beam computed tomography, cone-angle artifact, differentiable domain transform

Shengwang PENG, Yongbo WANG, Zhaoying BIAN, Jianhua MA, Jing HUANG. A dual-domain cone beam computed tomography reconstruction framework with improved differentiable domain transform for cone-angle artifact correction[J]. Journal of Southern Medical University, 2024, 44(6): 1188-1197.

Figures/Tables 11

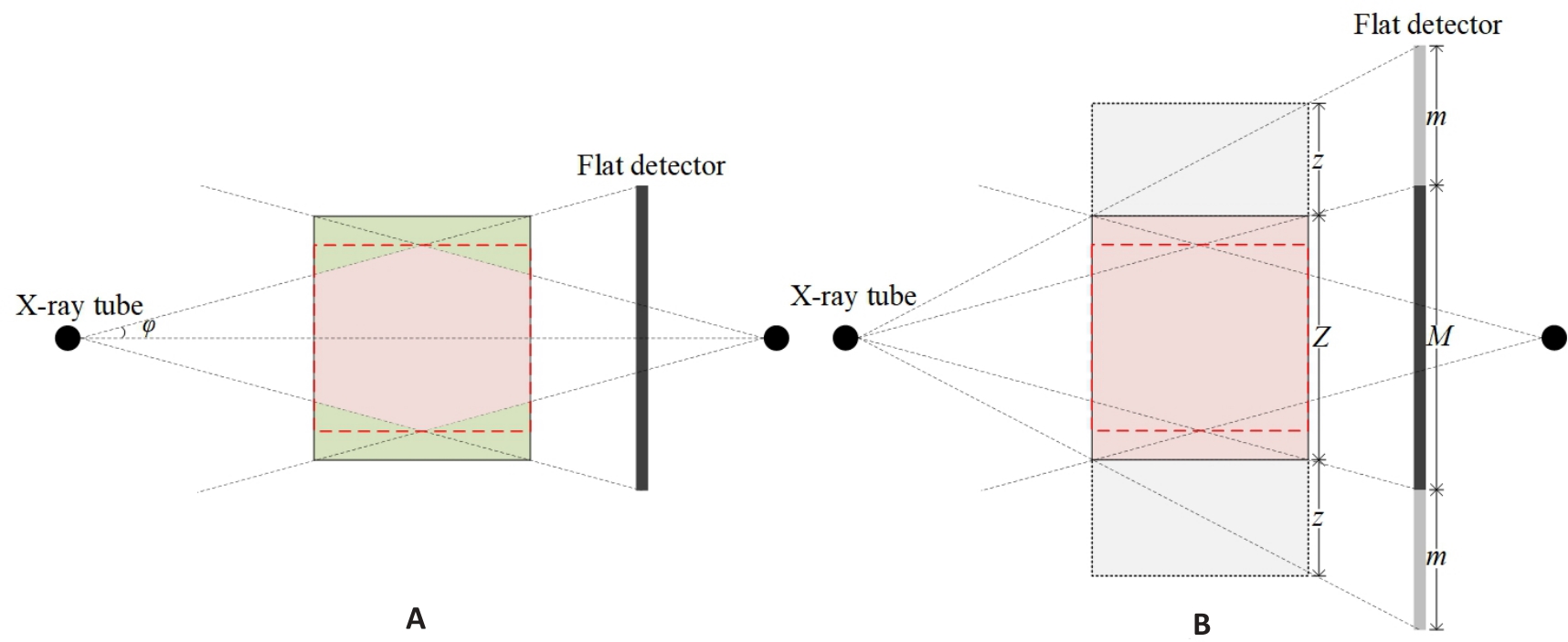
Fig.1 Initial and extended geometry of CBCT. A: Initial geometry of CBCT. φ: cone-angle. Pink and green zones represent the effective volume and missing volume, respectively. B: Extended geometry of CBCT. M: Number of detector rows; m: Extended number of detector rows in each ends; Z: Number of reconstructed slices; z: Number of extended reconstructed slices in both ends.

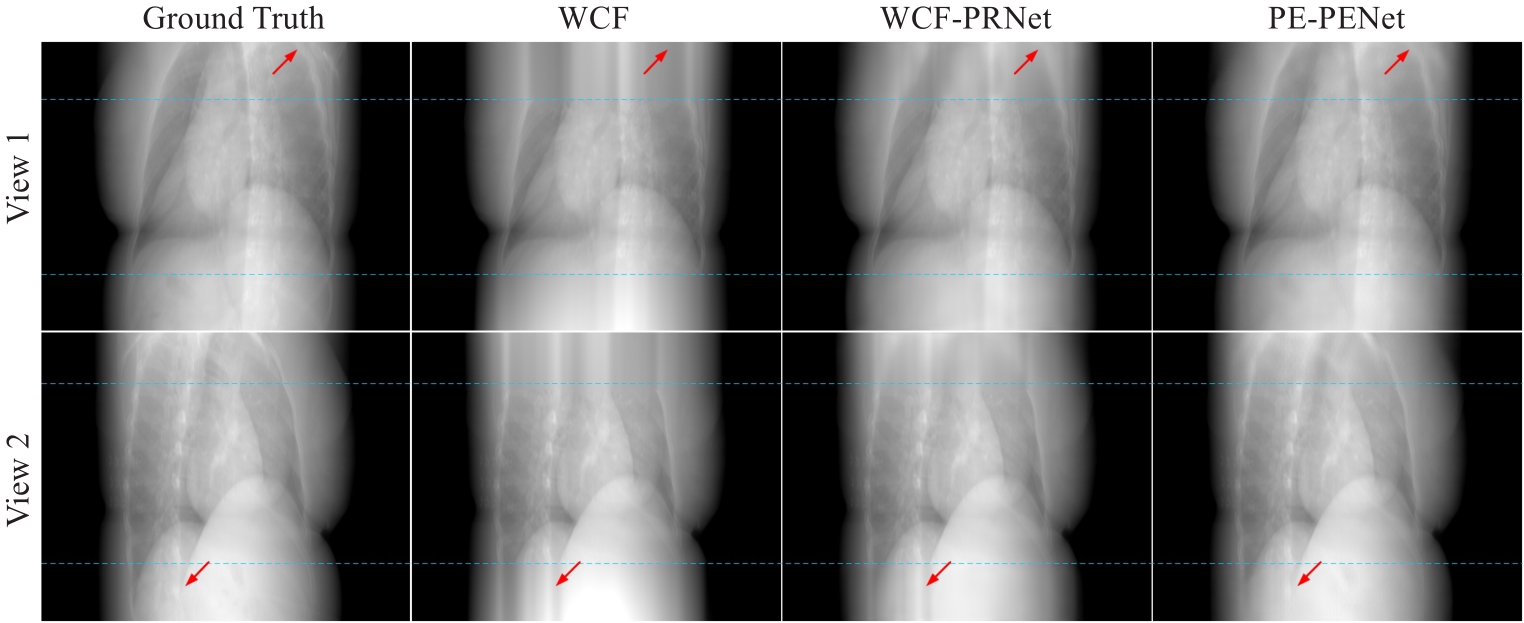
Fig.2 Overall architecture of the proposed DualCBR-Net. IDT represents the improved differentiable domain transform module.

Fig.3 Results of expanded projection data using different methods at two different views. The blue dashed lines at the top and bottom represent the 2 m rows of the projected data. The contrast regions are indicated by red arrows.

Tab.1 Quantitative comparison results of expanded projection data for different methods (Mean±SD)

Methods	PSNR	SSIM	RMSE
WCF	28.8022±2.5542	0.9650±0.0045	9.6567±2.7958
WCF-PRNet	40.1381±0.7931	0.9818±0.0023	2.5204±0.2356
PE-PRNet	45.9624±0.3935	0.9870±0.0013	1.2849±0.0582

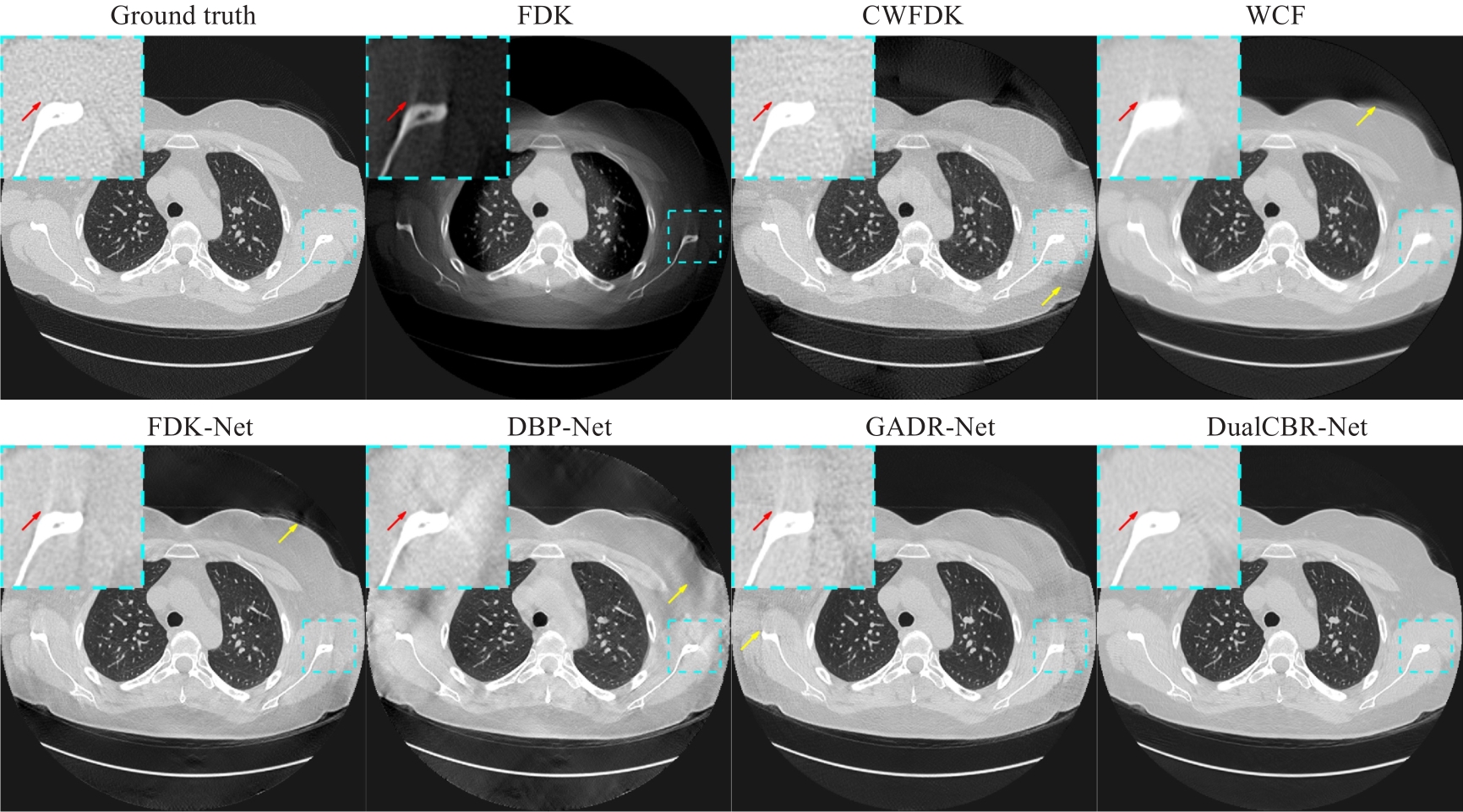
Fig.4 Ground truth image and reconstruction results with different methods in the axial plane. The dashed blue boxes highlight the enlarged region of interest. The display range is (-1150, 350) Hu. The contrast regions are indicated by red arrows and the artifact regions by yellow arrows.

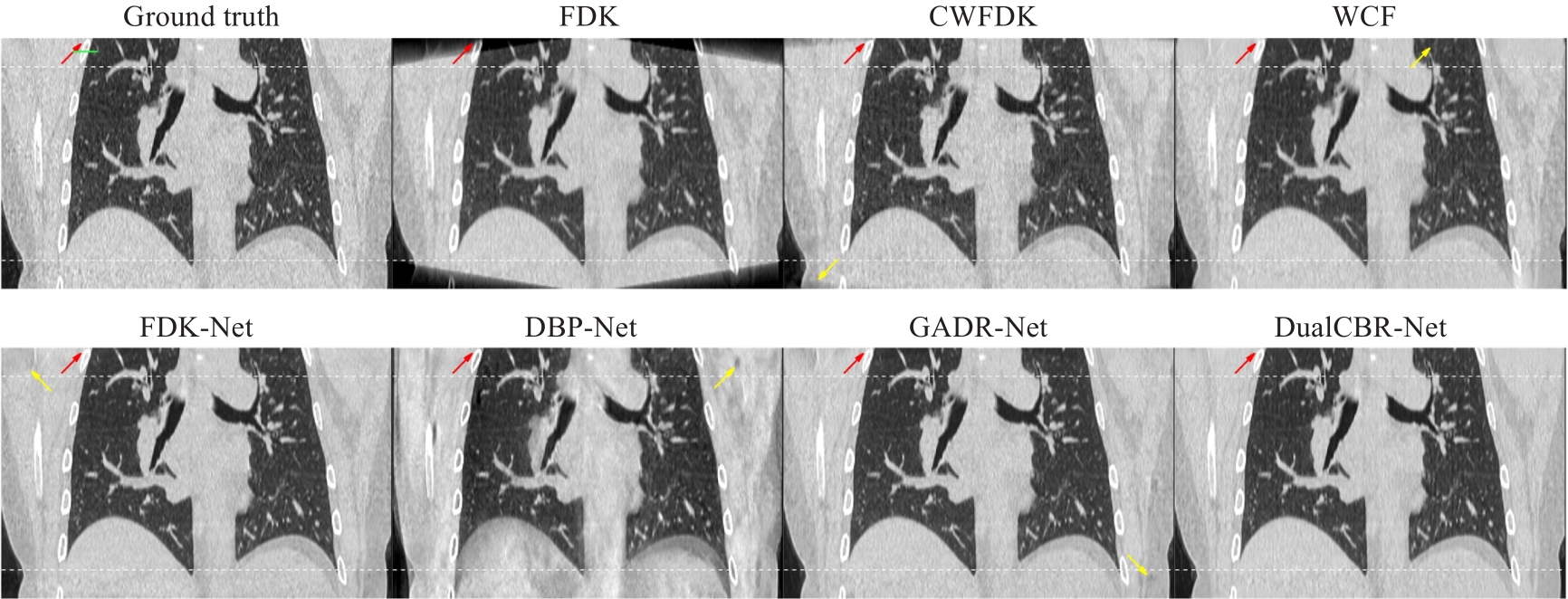
Fig.5 Ground truth image and reconstruction results with different methods in the coronal plane. The white curves at the top and bottom of the image indicate the regions affected by cone-angle artifacts. The display range is (-1150, 350) Hu. The contrast regions are indicated by red arrows and the artifact regions by yellow arrows.

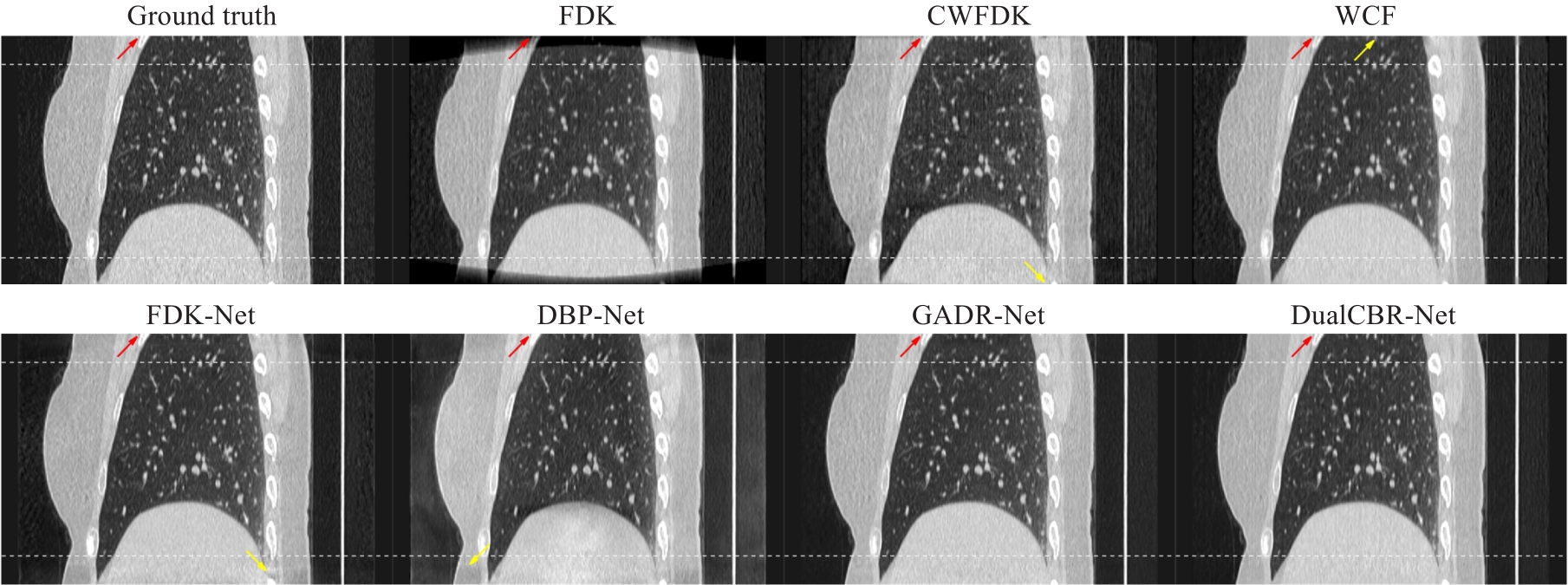
Fig.6 Ground truth image and reconstruction results with different methods in the sagittal plane. The white curves at the top and bottom of the image indicatethe regions affected by cone-angle artifacts. The display range is (-1150, 350) Hu. The contrast regions are indicated by red arrows and the artifact regions by yellow arrows.

Fig.7 Profile comparison between the ground truth image and different methods. The horizontal profile is indicated by green line in Fig.5.

Tab.2 Quantitative comparison results of cone-angle artifact removal performance for different methods (Mean±SD)

Methods	PSNR	SSIM	RMSE
FDK	31.7062±7.1703	0.8049±0.1469	10.6439±14.0262
CWFDK	33.7062±1.8418	0.8417±0.0323	5.3882±1.2773
WCF	34.7489±1.7365	0.8675±0.0284	4.7616±0.9647
FDK-Net	35.4597±2.0657	0.8769±0.0286	4.4279±1.1314
DBP-Net	30.7556±1.6946	0.8471±0.0236	7.5277±1.3869
GADR-Net	36.3036±1.6391	0.8871±0.0254	3.9708±0.7276
DualCBR-Net	36.9515±1.6658	0.8945±0.0280	3.6882±0.6994

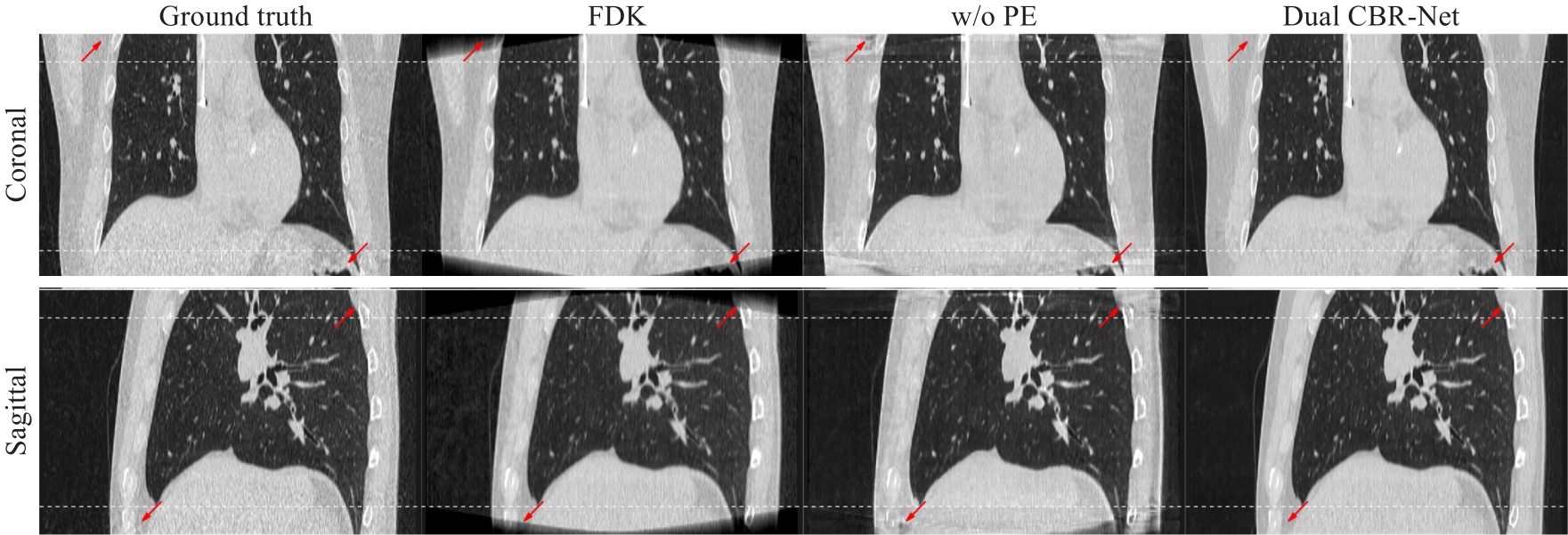
Fig.8 Validation results of the projection expansion strategy. The upper and lower rows are coronal plane and sagittal plane reconstruction images, respectively. The white curves at the top and bottom of the image indicated the regions affected by cone-angle artifacts. Projection extension strategy is not used for images in the "w/o PE" column. The display range was (-1150, 350) Hu. The contrast areas are indicated by red arrows.

Tab.3 Quantitative comparison results in ablation studies (Mean±SD)

Methods	PSNR	SSIM	RMSE
PENet	35.0010±1.2653	0.8523±0.0284	4.6987±0.6780
DualCBR-Net (w/o IRNet)	35.2349±1.1689	0.8695±0.0281	4.3842±0.6548
DualCBR-Net (w/o AM)	36.4023±1.5633	0.8825±0.0356	3.9054±0.5966
DualCBR-Net (4 slices)	36.5393±1.5784	0.8890±0.0325	3.8529±0.6498
DualCBR-Net (6 slices)	36.6722±1.6950	0.8901±0.0278	3.7021±0.6447
DualCBR-Net (10 slices)	36.2839±1.7725	0.8760±0.0252	4.0133±0.6561
DualCBR-Net (w/o $L s s i m$ )	36.4529±1.5612	0.8796±0.0265	3.9255±0.6846
DualCBR-Net	36.9515±1.6658	0.8945±0.0280	3.6882±0.6994

Tab.3 Quantitative comparison results in ablation studies (Mean±SD)

Methods	PSNR	SSIM	RMSE
PENet	35.0010±1.2653	0.8523±0.0284	4.6987±0.6780
DualCBR-Net (w/o IRNet)	35.2349±1.1689	0.8695±0.0281	4.3842±0.6548
DualCBR-Net (w/o AM)	36.4023±1.5633	0.8825±0.0356	3.9054±0.5966
DualCBR-Net (4 slices)	36.5393±1.5784	0.8890±0.0325	3.8529±0.6498
DualCBR-Net (6 slices)	36.6722±1.6950	0.8901±0.0278	3.7021±0.6447
DualCBR-Net (10 slices)	36.2839±1.7725	0.8760±0.0252	4.0133±0.6561
DualCBR-Net (w/o $L s s i m$ )	36.4529±1.5612	0.8796±0.0265	3.9255±0.6846
DualCBR-Net	36.9515±1.6658	0.8945±0.0280	3.6882±0.6994

References 36

1	Jaffray DA, Siewerdsen JH, Wong JW, et al. Flat-panel cone-beam computed tomography for image-guided radiation therapy[J]. Int J Radiat Oncol Biol Phys, 2002, 53(5): 1337-49.
2	Wang G, Zhao SY, Heuscher D. A knowledge-based cone-beam X-ray CT algorithm for dynamic volumetric cardiac imaging[J]. Med Phys, 2002, 29(8): 1807-22.
3	Pauwels R, Araki K, Siewerdsen JH, et al. Technical aspects of dental CBCT: state of the art[J]. Dentomaxillofac Radiol, 2015, 44(1): 20140224.
4	Feldkamp LA, Davis LC, Kress JW. Practical cone-beam algorithm[J]. J Opt Soc Am A, 1984, 1(6): 612.
5	Tuy HK. An inversion formula for cone-beam reconstruction[J]. SIAM J Appl Math, 1983, 43(3): 546-52.
6	Grass M, Köhler T, Proksa R. Angular weighted hybrid cone-beam CT reconstruction for circular trajectories[J]. Phys Med Biol, 2001, 46(6): 1595-610.
7	Tang X, Hsieh J, Nilsen RA, et al. A three-dimensional-weighted cone beam filtered backprojection (CB-FBP) algorithm for image reconstruction in volumetric CT-helical scanning[J]. Phys Med Biol, 2006, 51(4): 855-74.
8	Mori S, Endo M, Komatsu S, et al. A combination-weighted Feldkamp-based reconstruction algorithm for cone-beam CT[J]. Phys Med Biol, 2006, 51(16): 3953-65.
9	Grimmer R, Oelhafen M, Elstrøm U, et al. Cone-beam CT image reconstruction with extended z range[J]. Med Phys, 2009, 36(7): 3363-70.
10	Zhu L, Starman J, Fahrig R. An efficient estimation method for reducing the axial intensity drop in circular cone-beam CT[J]. Int J Biomed Imaging, 2008: 242841.
11	Hsieh J, Chao E, Thibault J, et al. A novel reconstruction algorithm to extend the CT scan field-of-view[J]. Med Phys, 2004, 31(9): 2385-91.
12	Hsieh J. Two-pass algorithm for cone-beam reconstruction[C]. San Diego: Medical Imaging 2000 : Image Processing, 2000: 533-40.
13	Han C, Baek J. Multi-pass approach to reduce cone-beam artifacts in a circular orbit cone-beam CT system[J]. Opt Express, 2019, 27(7): 10108-26.
14	Han Y, Kim J, Ye JC. Differentiated backprojection domain deep learning for conebeam artifact removal[J]. IEEE Trans Med Imaging, 2020, 39(11): 3571-82.
15	Minnema J, van Eijnatten M, der Sarkissian H, et al. Efficient high cone-angle artifact reduction in circular cone-beam CT using deep learning with geometry-aware dimension reduction[J]. Phys Med Biol, 2021, 66(13): 135015.
16	Xia WJ, Shan HM, Wang G, et al. Physics-/ Model-Based and Data-Driven Methods for Low-Dose Computed Tomography: a survey[J]. IEEE Signal Process Mag, 2023, 40(2): 89-100.
17	He J, Wang YB, Ma JH. Radon inversion via deep learning[J]. IEEE Trans Med Imaging, 2020, 39(6): 2076-87.
18	He J, Chen SL, Zhang H, et al. Downsampled imaging geometric modeling for accurate CT reconstruction via deep learning[J]. IEEE Trans Med Imaging, 2021, 40(11): 2976-85.
19	Würfl T, Hoffmann M, Christlein V, et al. Deep learning computed tomography: learning projection-domain weights from image domain in limited angle problems[J]. IEEE Trans Med Imag, 2018, 37(6): 1454-63.
20	Hu DL, Liu J, Lv TL, et al. Hybrid-domain neural network processing for sparse-view CT reconstruction[J]. IEEE Trans Radiat Plasma Med Sci, 2021, 5(1): 88-98.
21	Zhang YK, Hu DL, Zhao QL, et al. CLEAR: comprehensive learning enabled adversarial reconstruction for subtle structure enhanced low-dose CT imaging[J]. IEEE Trans Med Imag, 2021, 40(11): 3089-101.
22	Yang QS, Yan PK, Zhang YB, et al. Low-dose CT image denoising using a generative adversarial network with Wasserstein distance and perceptual loss[J]. IEEE Trans Med Imaging, 2018, 37(6): 1348-57.
23	Ronneberger O, Fischer P, Brox T. U-net: convolutional networks for biomedical image segmentation[EB/OL]. [2015-05-18]. .
24	Guo MH, Xu TX, Liu JJ, et al. Attention mechanisms in computer vision: a survey[J]. Comput Vis Medium, 2022, 8(3): 331-68.
25	Moen TR, Chen BY, Holmes DR 3rd, et al. Low-dose CT image and projection dataset[J]. Med Phys, 2021, 48(2): 902-11.
26	van Aarle W, Palenstijn WJ, De Beenhouwer J, et al. The ASTRA Toolbox: a platform for advanced algorithm development in electron tomography[J]. Ultramicroscopy, 2015, 157: 35-47.
27	Kingma DP, Ba J. Adam: a method for stochastic optimization[EB/OL]. [2014-12-22].
28	Jin KH, McCann MT, Froustey E, et al. Deep convolutional neural network for inverse problems in imaging[J]. IEEE Trans Image Process, 2017, 26(9): 4509-22.
29	Parker DL. Optimal short scan convolution reconstruction for fanbeam CT[J]. Med Phys, 1982, 9(2): 254-7.
30	Lee D, Choi S, Kim HJ. High quality imaging from sparsely sampled computed tomography data with deep learning and wavelet transform in various domains[J]. Med Phys, 2019, 46(1): 104-15.
31	Zhou B, Chen XC, Zhou SK, et al. DuDoDR-Net: dual-domain data consistent recurrent network for simultaneous sparse view and metal artifact reduction in computed tomography[J]. Med Image Anal, 2022, 75: 102289.
32	Chao LY, Wang ZW, Zhang HB, et al. Sparse-view cone beam CT reconstruction using dual CNNs in projection domain and image domain[J]. Neurocomputing, 2022, 493(7): 536-47.
33	Chen DD, Tachella J, Davies ME. Equivariant imaging: learning beyond the range space[C]. Montreal: 2021 IEEE/CVF International Conference on Computer Vision, 2021: 4359-68.
34	Chen DD, Tachella J, Davies ME. Robust Equivariant Imaging: a fully unsupervised framework for learning to image from noisy and partial measurements[C]. New Orleans, 2022 IEEE/CVF Conference on Computer Vision and Pattern Recognition, 2022: 5637-46.
35	Peng SW, Liao JY, Li DY, et al. Noise-conscious explicit weighting network for robust low-dose CT imaging[C]. San Diego: Medical Imaging 2023 : Physics of Medical Imaging, 2023: 711-8.
36	Chen J, Zhang R, Yu T, et al. Label-retrieval-augmented diffusion models for learning from noisy labels[J]. Adv Neural Inf Process Syst, 2024, 36. doi: 10.48550/arXiv.2305.19518

[1]	. Design and optimization of a cone-beam CT system for extremity imaging [J]. Journal of Southern Medical University, 2018, 38(11): 1331-.
[2]	. Cone-beam computed tomography for determination of mesial root canal curvatures of human mandibular first molars [J]. Journal of Southern Medical University, 2018, 38(07): 824-.
[3]	. Motion-compensated compressed sensing four-dimensional cone-beam CT reconstruction [J]. Journal of Southern Medical University, 2016, 36(07): 969-.