2南方医科大学第三附属医院骨科,广东 广州 510630
2Department of Orthopedic Surgery, Third Affiliated Hospital of Southern Medical University, Guangzhou, 510630, China
随着数字医学技术与计算机硬件技术的快速发展, 有限元法作为一种离散数值计算方法已被广泛用于骨科生物力学领域[1]。在过去数十年中,如何获得更为合理的材料属性赋值和更为精确的几何模型一直是骨科生物力学有限元分析的热点问题[2, 3]。目前,对于骨骼有限元建模的材料参数赋值方法主要有两种,一种是采用复合结构建模的均一赋值方法,另一种是基于CT灰度经验公式的非均匀赋值法[4, 5, 6]。前者将皮质骨和松质骨分别简化作均一属性的材料,赋值过程简便、快速,可对模型进行各种空间位置变换操作,但模型的简化赋值可能导致最终分析结果准确性不足;而后者属于原位赋值方法,具有个体化建模的特点,但难以进行模型的虚拟操作(如截骨矫形、虚拟复位等)[4]。然而,同时兼具上述两种方法优点的有限元建模方法在国内未见报道。为此,本文以胫骨外旋扭转畸形病例数据为应用范例,探索一种新的有限元建模方法以满足截骨矫形仿真分析的需求。
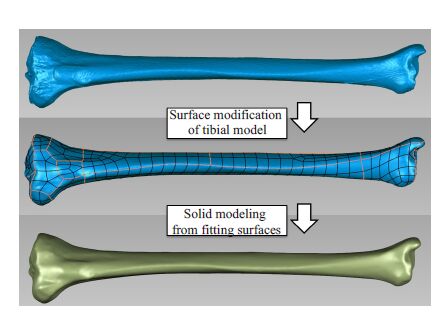
1 材料和方法 1.1 数据采集及胫骨实体模型的三维重建选取1名成人右侧胫骨外旋扭转畸形病例作为数据采集来源,采用64排螺旋CT机(西门子,德国)沿胫骨干长轴方向进行CT扫描,范围覆盖膝关节及踝关节,扫描层距为1 mm,共获得连续横断面1000张512×512像素的CT图像,并将获得的CT图像以通用的DICOM标准格式导入Mimics 14.0 软件(Materialise,比利时)进行胫骨模型三维重建,参考既往文献的标准测量方法在三维模型上测得胫骨外旋角度为41.8°,符合扭转畸形诊断的解剖参数标准[7],导出为STL文件保存。 将STL文件导入逆向工程软件Geomagic Studio 2012 (Geomagic,美国)中进行降噪和光顺表面处理,进而构建出胫骨实体模型,过程如图1所示。
|
图1 胫骨三维模型的表面处理与实体建模 Fig.1 Surface treatment and solid modeling of the 3D tibia model. |
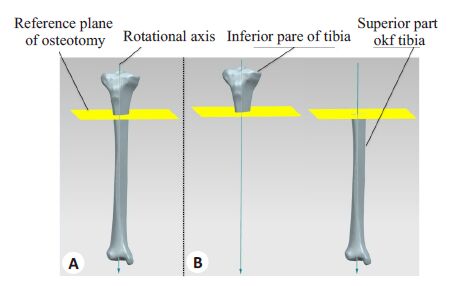
将胫骨实体模型导入三维建模软件UG NX 8.5(西门子,德国)中确定胫骨上部干骺端的截骨平面并以此建立参考平面,同时以拟合的胫骨长轴作为截骨旋转轴并建立相应的空间直线,以参考平面对胫骨进行虚拟截骨操作,获得截骨后上下两个部件子模型,并以此作为划分单元网格的对象(图2)。
|
图2 胫骨截骨平面的建立(A)与虚拟截骨操作(B) Fig.2 Simulation of osteotomy on the tibia model. A: Definition of the plane of osteotomy; B: Process of simulative osteotomy. |
将旋转操作前的各部胫骨子模型导入有限元分析软件Abaqus 6.14(达索,法国)中划分网格后并以inp文件格式导入Mimics软件中进行材料属性赋值,设定图像CT值HU与表观密度、表观密度与弹性模量的关系公式[4]后,完成基于CT图像灰度的原位赋值过程,最后以inp格式把胫骨上下部分子模型导回至有限元软件前处理模块中(图3)。

|
图3 基于CT灰度-材料属性关系公式赋予胫骨非均匀材料属性 Fig.3 Uneven material property assignment of the tibia based on the relationship between CT gray values and material properties. |
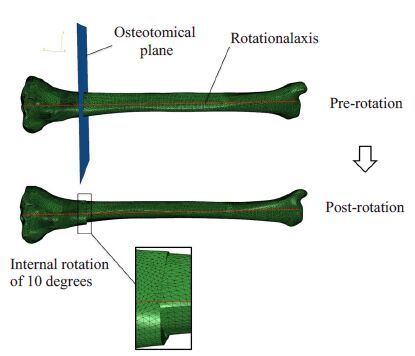
将先前定义好的参考轴模型导入Abaqus软件中, 在装配模式下按照预先规划的10°内旋角度,对胫骨下部模型沿着参考旋转轴进行旋转位置变换操作,对截骨平面设置为Tie约束,得到调整位置后完整的胫骨旋转截骨重装配模型(图4)。参照文献数据[8],在胫骨上端施加20 Nm的扭矩载荷,固定胫骨远端踝关节平面作为模型边界条件,最后提交至求解器计算分析截骨后的应力和位移分布结果。至此,整个建模分析过程全部完成(图5)。
|
图4 完成材料属性赋值后的胫骨虚拟旋转截骨操作 Fig.4 Simulated rotational osteotomy of the tibia after properties assignment. |
|
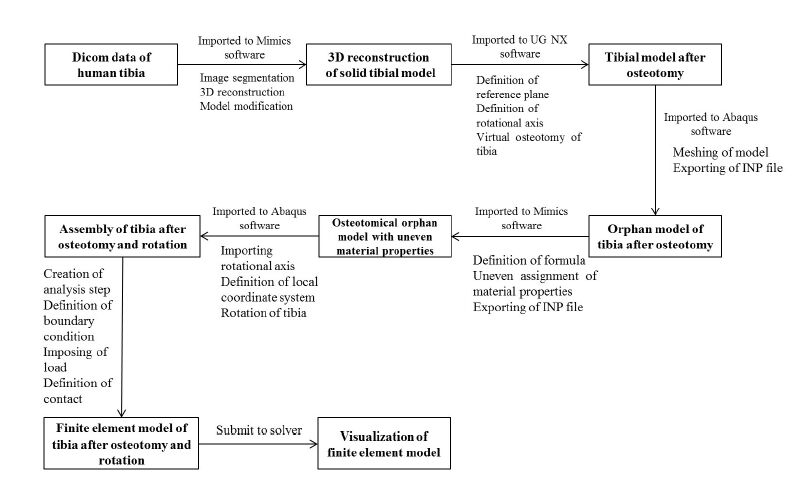
图5 建模分析方法流程图 Fig.5 Flow chart of modeling and analysis. |
通过CT灰度值赋值法建立的胫骨旋转截骨矫形有限元模型可顺利提交分析,并得到胫骨旋转截骨后的应力和位移分布结果(图6)。在胫骨上段施加20 Nm 的扭矩载荷作用下,对于胫骨的应力分布方面,旋转截骨后的应力分布云图显示(图6A Ⅰ~Ⅱ),最大应力峰值主要分布在胫骨旋转截骨平面部位,应力峰值为306.8 MPa;当忽略截骨平面部位后(图6A Ⅲ~Ⅳ),胫骨最大应力分布在胫骨中下段,最大应力峰值为56.83 MPa; 对于位移分布方面(图6B Ⅰ~Ⅳ),同样扭矩作用载荷下,胫骨的最大位移分布主要位于胫骨上段,最大合位移峰值为2.15 mm,其中X和Y方向位移分量为主要位移分量,最大峰值分别为1.063 mm和2.005 mm,Z方向位移分量的最大峰值为0.123 mm。
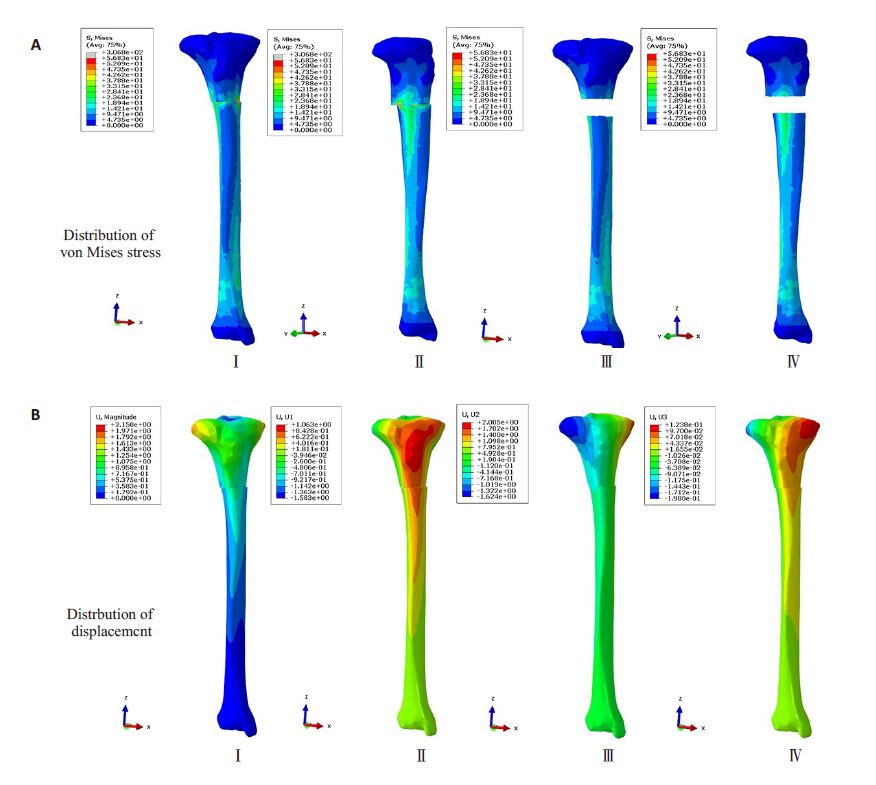
|
图6 扭矩作用下胫骨应力分布云图(A)和胫骨位移分布云图(B) Fig.6 Results of finite element analysis of tibia under torque. A: Distribution of stress; B: Distribution of displacement. |
在建模方法方面,有限元分析的准确性很大程度上取决于建模过程的合理性,而骨骼材料属性的赋值是骨骼有限元分析中的关键环节,也是有限元模型计算分析结果可靠性的保证。本研究采用了非均质材料赋值的建模方法构建了胫骨有限元模型,在理论上更为接近人体骨骼材料的力学特性,可使模型的分析计算具有较高的可靠性。这一方法在国内外的文献报道中均已得到了应用,同时也得到了体外生物力学实验的文献数据支持[9, 10]。相比之下,以往也有部分人体骨骼的有限元研究对骨骼的材料属性作均匀分布简化处理,将骨骼模型简单划分为密质骨和松质骨两种材料进行赋值[6]。该方法仅包括了三维重建、虚拟装配和有限元前处理3个部分,在一定程度上提高了分析建模的效率。然而,对于骨密度差异较小的模糊交界区域采用均一赋值处理将在一定程度上人为提高或降低整体骨骼的结构刚度, 从而影响最终的分析结果精度,对比骨骼真实应变情况容易产生较大偏差,这将给不同模型分组之间的有限元对比分析结果带来了显著的不稳定性[11];而本研究采用的非均匀材料赋值方法涉及了多个建模软件之间的文件交互对接,步骤程序相对细化,尽管影响了建模过程的效率,但可获得更为接近人体骨骼真实材料性质的模型,有效提高有限元分析结果的稳定性。
在Mimics软件中,用户能根据骨骼CT图像中不同区域的灰度值按经验公式赋予模型非均匀的材料属性[4, 12, 13, 14, 15, 16]。非均匀赋值方法可以全面分析骨组织复杂的密度变化情况,基于此法的有限元分析结果具有更高的准确度[17, 18]。然而,这一方法要求网格模型空间位置须和原有CT图像覆盖范围保持一致,当模型空间位置发生变化时,原位CT灰度赋予材料属性的方法将完全失效,因此应用既往方法将无法在截骨矫形后的骨骼有限元分析中应用。因此,本研究提出的建模技术路线,有效解决了既往方法不能直接对模型位置变换后的赋值问题。笔者以胫骨扭转畸形截骨分析为应用实例,利用不同软件之间的模型文件转换接口,实现了材料原位赋值和虚拟截骨之间的兼容,形成一套新的有限元建模流程。尽管国外已有研究机构自主研发了相应的映射配对方法来解决这一问题,该方法尚不能很好地解决局部网格单元缺失的问题[19]。因此,本研究的技术方案相对更为简单高效,适用性较强。
在分析结果方面,本研究方法构建的有限元模型可顺利提交分析,从应力和位移分布的云图来看,计算结果较为接近临床实际情况,扭转刚度数值也较为接近以往文献数据[8]。从整个建模过程上看,本研究基本实现了胫骨旋转截骨矫形术后的生物力学预测分析,在保证各部份骨骼按CT灰度值赋值法进行非均匀材料属性赋值的前提下,截骨后的骨骼各部也能根据术前设计参考轴面及角度实现准确的旋转截骨,从而满足了骨骼矫形手术的有限元仿真分析需求。从结果上看,本研究在对胫骨上段施加扭矩载荷的作用下,在截骨平面部位产生了较大的应力集中现象,最大峰值达到了306.8 MPa, 造成这一结果的原因主要是因为本研究并未考虑截骨术后早期的内固定器械对模型支撑效应,同时未对截骨矫形的后期截骨平面骨愈合形态进行模拟,因此仅仅对截骨平面的相邻单元节点进行了绑定约束,从而形成了截骨平面单元节点之间形成了刚性连接,使得结果出现了较高的应力峰值。通过忽略截骨面高应力单元可消除截骨面绑定约束设定对结果的影响,由此获得的应力分布特点更为合理,而大体应力数值水平也与文献报道同等载荷下的分析结果基本一致。因此,本模型分析结果基本符合临床实际情况。而在实际分析中,应用本方法建模时应明确模型是处于截骨矫形术后的哪一个时期,明确是否存在相应的植入物共同承担生理载荷和骨折愈合情况,并根据实际情况调整模型设定。
总的来说,本研究提出的建模方法在应用拓展性方面显示出一定的优势:首先,本方法可用于不同骨密度水平的活体个体化矫形外科生物力学预测分析;其次, 实施过程中采用的建模软件均为现有可用的商业建模软件,不需要自行开发空间映射配对赋值软件,简化了建模过程,具有较高的可操作性。然而,本研究在模型的定量评价方面也存在着一定的局限性。目前,模型的定量评价主要有同期生物力学实验验证、文献数据验证和临床验证3种方式。第1种方式是利用尸体标本的实验生物力学数据对模型进行定量评估,而在本研究中建立的胫骨模型源于扭转畸形患者的CT扫描数据,因此生物力学实验无法在该患者胫骨上实施。而获取骨骼畸形的尸体标本极为困难,同样导致实验定量评估难以开展。对于第2种方式,与本研究相关的胫骨扭转畸形分析鲜有文献报道,且既往研究中的个体和本研究中的患者个体存在着一定的解剖差异,因而可比性受到一定的影响。而本研究选取了同样载荷条件下的正常胫骨分析文献数据进行对比,尽管正常胫骨与扭转畸形胫骨存在着结构上的差异,但本研究中整体胫骨的应力分布特点和数值基本处于合理范围,这在一定程度上验证了模型的有效性。而对于第3种方式,本胫骨模型的高应力区主要位于胫骨截面发生明显变化的中下1/3部位,该部位是临床上胫骨骨折发生的最常见部位,说明模型大体符合临床实际情况。而在后续的研究中,采用活体动物骨骼畸形造模的方法有望解决上述定量评估问题,但活体验证实施时间较长,且受物种之间解剖结构差异的影响,同样存在一定的局限性。而通过活体的放射立体照相测量分析(RSA)和有限元分析相结合的方式,有望为模型临床评估提供一种更为理想的手段[20]。
本研究提出了一种基于现有医学三维建模软件的骨骼有限元建模方法,并以一例胫骨扭转畸形病例的旋转截骨矫形有限元分析介绍了该方法的应用。结果表明,该方法实现了骨骼CT图像灰度-材料参数赋值的同时,还可进行模型空间位置变换操作,因而可为临床截骨矫形手术的有限元分析预测提供简单、可靠和准确的建模手段。
| [1] |
刘长剑, 罗宗键. 有限元及显微有限元分析在骨科应用的新进展[J]. 大连医科大学学报, 2014(2): 182-5. ( 1) 1)
|
| [2] |
苏佳灿, 张春才, 陈学强, 等. 骨盆及髋臼三维有限元模型材料属性设定及其生物力学意义[J]. 中国临床康复, 2005, 9(2): 71-3. ( 1) 1)
|
| [3] |
Taddei F, Pancanti A, Viceconti M. An improved method for the automatic mapping of computed tomography numbers onto finite element models[J]. Med Eng Phys, 2004, 26(1): 61-9. ( 1) 1)
|
| [4] |
Lengsfeld M, Schmitt J, Alter P, et al. Comparison of geometrybased and CT voxel-based finite element modelling and experimental validation[J]. Med Eng Phys, 1998, 20(7): 515-22. ( 4) 4)
|
| [5] |
Completo A, Duarte R, Fonseca F, et al. Biomechanical evaluation of different reconstructive techniques of proximal tibia in revision total knee arthroplasty: An in-vitro and finite element analysis[J]. Clin Biomech (Bristol, Avon), 2013, 28(3): 291-8. ( 1) 1)
|
| [6] |
Vulovic S, Korunovic N, Trajanovic M, et al. Finite element analysis of CT based femur model using finite element program PAK[J]. J Serbian Society Comput Mech, 2011, 5(2): 160-6. ( 2) 2)
|
| [7] |
孙铁铮, 吕厚山, 倪磊, 等. 膝关节骨关节炎患者胫骨扭转角度的异常及临床意义[J]. 中华关节外科杂志: 电子版, 2007, 1(4): 242-6. ( 1) 1)
|
| [8] |
Gray HA, Taddei F, Zavatsky AB, et al. Experimental validation of a finite element model of a human cadaveric tibia[J]. J Biomech Eng, 2008, 130(3): 031016. ( 2) 2)
|
| [9] |
张美超, 焦培峰. 骨科三维有限元力学仿真的建模[J]. 中华创伤骨科 杂志, 2013, 15(1): 10-2. ( 1) 1)
|
| [10] |
Oshkour AA, Abu Osman NA, Davoodi MM, et al. Finite element analysis on longitudinal and radial functionally graded femoral prosthesis[J]. Int J numer method biomed eng, 2013, 29(12): 1412-27. ( 1) 1)
|
| [11] |
张国栋, 廖维靖, 陶圣祥, 等. 股骨有限元分析赋材料属性的方法[J]. 中国组织工程研究与临床康复, 2009, 13(43): 8436-41. ( 1) 1)
|
| [12] |
黄华军, 张国栋, 欧阳汉斌, 等. 基于3D打印技术的复杂胫骨平台骨折内固定手术数字化设计[J]. 南方医科大学学报, 2015, 35(2): 218-22. ( 1) 1)
|
| [13] |
严斌, 张国栋, 吴章林, 等. 3D打印导航模块辅助腰椎椎弓根螺钉精确植入的实验研究[J]. 中国临床解剖学杂志, 2014, 32(3): 252-5. ( 1) 1)
|
| [14] |
张国栋, 毛文玉, 廖维靖, 等. 基于三维重建技术及有限元分析的脊柱骨密度测量及其意义[J]. 中国临床解剖学杂志, 2010, 28(1): 78-84. ( 1) 1)
|
| [15] |
黄菊英, 李海云, 吴浩. 腰椎间盘突出症力学特征的仿真计算方法 [J]. 医用生物力学, 2012, 27(1): 96-101. ( 1) 1)
|
| [16] |
Huang H, Xiang C, Zeng C, et al. Patient-specific geometrical modeling of orthopedic structures with high efficiency and accuracy for finite element modeling and 3D printing[J]. Australas Phys Eng Sci Med, 2015, 38(4): 743-53. ( 1) 1)
|
| [17] |
Helgason B, Taddei F, Pálsson H, et al. A modified method for assigning material properties to FE models of bones[J]. Med Eng Phys, 2008, 30(4): 444-53. ( 1) 1)
|
| [18] |
O'reilly MA, Whyne CM. Comparison of computed tomography based parametric and patient-specific finite element models of the healthy and metastatic spine using a mesh-morphing algorithm[J]. Spine (Phila Pa 1976), 2008, 33(17): 1876-81. ( 1) 1)
|
| [19] |
Synek A, Chevalier Y, Baumbach SF, et al. The influence of bone density and anisotropy in finite element models of distal radius fracture osteosynthesis: Evaluations and comparison to experiments [J]. J Biomech, 2015, 48(15): 4116-23. ( 1) 1)
|
| [20] |
Madanat R, M?kinen TJ, Moritz N, et al. Accuracy and precision of radiostereometric analysis in the measurement of three-dimensional micromotion in a fracture model of the distal radius[J]. J Orthop Res, 2005, 23(2): 481-8. ( 1) 1)
|
 2016, Vol. 36
2016, Vol. 36
