2南方医科大学广东省医学图像处理重点实验室,广东广州 510515
Guangdong Provincial Key Laboratory of Medical Image Processing2, Southern Medical University, Guangzhou 510515, China
流行病学资料显示[1],肺癌是我国第一高发的恶性肿瘤,肺癌死亡率已占城市中癌亡的首位,发病率也比10年前翻了一倍。肺癌发病时病期相对较晚,放射治疗是主要治疗手段之一[2]。
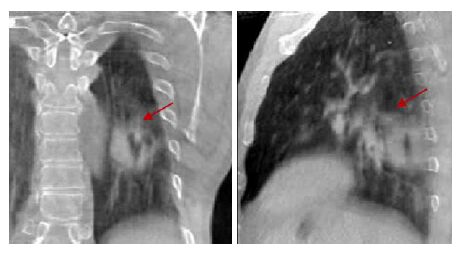
近年来,随着放射生物学、放射物理学的极速发展图像引导放疗(IGRT)技术的产生为肺部肿瘤精确放疗提供了可能[3]。目前,IGRT 类型较多,以锥形束CT (CBCT)引导的放疗系统为最具代表性[4],它直接整合到直线加速器上,治疗中可在治疗位置进行透视、摄片、 容积成像,继而在线调整治疗图像与计划图像的位置, 减少摆位误差,以期实现精确放疗的目标[5]。当前,临床肿瘤放射治疗多采用3D-CBCT引导的三维适形放射治疗技术。然而,对于胸腹部位置的肿瘤,为实现精确放疗,仅消除摆位误差是不够的,呼吸运动、心脏与大血管搏动以及食管蠕动均会引起肺部肿瘤的移动,其中呼吸运动的影响最为主要[6]。呼吸运动会导致重建CBCT 图像中出现严重的伪影及模糊,为纠正呼吸运动的影响,实现自由呼吸状态下的肿瘤的实时监测,近年来, 4D-CBCT 的概念被提出[7, 8]。然而,基于现有机载CBCT成像系统,因其转速有限,对于特定呼吸时相获取投影数目过少,常规解析重建算法尚无法重建出高清晰、无伪影的图像来完成肺部肿瘤的准确定位及在治疗时的三维运动轨迹跟踪(图1)。
|
图1 利用CBCT旋转一周全部投影数据重建所得3D-CBCT(多个呼吸相位平均)图像,肿瘤边界不清,存在运动模糊和伪影 Fig.1 3D-CBCT image reconstructed from the full projection with blurs and artifacts on the edge. |
近年来,为实现4D-CBCT的优质重建,在软件法方面,主流的研究方法可以归为两大类:基于运动补偿的重建算法[9, 10]和基于呼吸相关(Respiratory Correlated,RC)的重建算法[11, 12, 13]。基于运动补偿的重建算法将4D-CBCT 看作一个整体,利用全部投影和各呼吸相位图像间的运动信息进行重建。其中,由投影数据或者图像本身估计所得的呼吸运动矢量场(MVFs)直接应用于重建图像,而现有的算法对其估计一般不准确,易导致运动模糊校正不彻底或者伪结构的存在。另一类为基于RC重建算法,该类算法利用对应呼吸相位的投影数据进行该相位CBCT图像重建。该类算法属于不完全数据或者稀疏角度CT 重建范畴。针对此类型的问题,近年来各种算法相继出现,例如,随着CS理论的发展,Sidky 等[11]提出一种ASD-POCS 算法用于4D-CBCT 重建,取得了不错的效果,条形伪影得到有效抑制,但与此同时图像出现过平滑现象或阶梯效应。Chen 等[13]利用全部投影数据重建图像作为先验图像,提出了PICCS 算法,该算法有效的融入先验图像信息,重建所得单相位图像伪影得到有效抑制,但先验图像中的模糊伪影和某些虚假解剖结构将有可能传播至待重建图像,影响最终重建图像质量。基于呼吸相关的4D-CBCT重建算法由于投影数据严重缺失的本质,导致其重建图像质量不高,且现有的研究大多局限于相对简单的体模研究,对于肺部复杂解剖结构,此类方法重建图像中细微结构有可能会丢失或产生畸变。
本文中,我们拟将整个呼吸周期的4D-CBCT 看作整体,充分考虑各呼吸相位图像之间的相关特性, 构建用于迭代重建的数据保真模型,并基于压缩感知理论,引入全变分正则化先验,形成基于运动补偿的压缩感知重建算法。文中,我们将利用物理体模数据及临床数据对算法进行性能测试。
1 方法 1.1 基于运动补偿的压缩感知4D-CBCT重建模型构建假设整个呼吸周期可分为P个呼吸相位,临床上该值一般设定为8-10.4D-CBCT 可以定义为f = {f1;f2…fT} ∈ RNP ,其中N 表示一个呼吸相位下3D-CBCT 体数据体素个数. 对于单个呼吸相位,CBCT 的成像模型可以用下式表示:
| \[{g_i} = {H_i}{f_i},i = 1,2, \cdots P\] | (1) |
式(1)中,gi表示对应于呼吸相位i的投影数据,Hi该呼吸相位下对应的系统矩阵,fi为待估计图像。CBCT 图像的重建即由已经获得的投影数据gi及相应的系统矩阵Hi 对式(1)进行反问题求解。4D-CBCT中个呼吸时相下投影数据不完整的特点,使得式(1)的求解成为一个病态逆问题。
本文中,引入不同呼吸相位图像间的相关特性,我们拟将原CBCT成像模型写为:
| ${g_i} = {H_i}{M_{i,k}}{f_k},i = 1,2, \cdots P;k = 1,2, \cdots P$ | (2) |
其中,假设fk为对应呼吸相位k的CBCT图像,利用相位k 和j图像间的变形场,可以得到Mi,k fk≈fj,Mi,k为图像fk 到fj的运动补偿算子。因此,通过式(2)我们可将不同呼吸相位的图像进行关联,在估计相位k对应CBCT图像时,引入其它相位对应的投影数据以增加代价函数保真项的可靠性,同时,为保持图像的边缘特性及去除模糊效应,我们引入全变分正则化的方法,构建如下代价函数:
| $\min \mathop {imize}\limits_{{f_k}} \sum\limits_{i = k - m}^{k + m} {{a_i}||} {H_i}{M_{i,k}}{f_k} - {g_i}|| + \lambda ||f|{|_{TV}}$ | (3) |
式(3)中,ai为权重因子,表征相位k与相位i图像的相关程度,由于呼吸运动为周期性的,因此,本文中,与呼吸相位k相临近的(如吸气中期与吸气末端),给予较大权重,与呼吸相位k相背离的(如呼气末端与吸气末端),给予较小的权重,当i = k时ai=1,参数m表示与相位k相近邻的2m个呼吸相位。λ为正则化参数,用来调节数据保真项与正则化项间的权重比例。本文中,采用各向同性全变分来构建正则化,基于TV/L1 的正则化可以表示为:
| $||f|{|_{TV}} = \sqrt[{\mathop \Sigma \limits_j }]{{\left[ {{D_x}{f_k}} \right]_j^2 + \left[ {{D_y}{f_k}} \right]_j^2 + \left[ {{D_z}{f_k}} \right]_j^2}}$ | (4) |
其中Dx ,Dy ,Dz 为沿着横向、纵向、Z 轴方向的前向差分投影算子,定义为:
| $\begin{array}{l} {D_x}{f_k} = vec\left( {{f_k}(x + 1,y,z)} \right) - {f_k}(x,y,z),\\ {D_y}{f_k} = vec\left( {{f_k}(x,y + 1,z)} \right) - {f_k}(x,y,z),\\ {D_z}{f_k} = vec\left( {{f_k}(x,y,z + 1)} \right) - {f_k}(x,y,z) \end{array}$ | (5) |
式(3)中,不同相位图像间运动变形场的准确估计对重建图像的质量起着至关重要的作用。本文中,我们采用光流法对呼吸运动进行估计。三维光流法(3D-OFM)是一种重要的分析运动图像的可变形图像配准方法,它的计算是基于图像像素进行,在精确性和鲁棒性方面有很大的优势。本文中所用光流法为霍恩- 舒克(Horn﹠Schunck)提出的算法[14]。对于一个物理点的位置(x,y,z)在一个参考相位k和它的位置在任何其他相位的i的对应关系可用一个变形模型定义:
| ${f_k}(x + u,y + v,z + s) = {f_i}(x,y,z)$ | (6) |
(u,v,s)为图像fk与fi之间的光流场,将待配准的图像按照光流进行变换即可得到配准图像。转化为算子形式,即为Mi,k fk = fi。理论上任何相位的CBCT体数据fi均可由fk及对应光流场变形配准获取,且该过程具有可逆性。
本文提出的算法是基于重建图像本身进行运动估计/补偿的,因此,图像重建和运动变形估计是协同进行的,在此我们需要指出,最初重建图像中含有较多的噪声及伪影,初始运动估计信息的可能不准确,但随着迭代次数的增加,重建图像质量的逐步提升,该效应会逐步减弱。
1.3 算法优化求解对于代价函数(3)式的求解,由于其复杂性及维度比较高,因此本文中我们利用(Gradient-Projection- Barzilai-Linesearch,GPBL)算法[15]进行迭代优化。对于特定的相位k,其优化具体过程如下:
对于k = 1,2,…P,执行
Step(1):$g_k^{(n)} \leftarrow \sum\limits_{i = k - m}^{k + m} {{a_i}M_i^TH_i^T({H_i}{M_{i,k}}f_k^{n - 1} - {g_i}) + \lambda } \nabla ||D{f_k}|{|_{\ell 1}}$
Step (2):对于所有的像素点j :如果满足f(n-1)(j)≥0,g(n)(j)≤0,执行pk(n) =gk(n)
否则pk(n)(j)=0
Step(3):${\eta ^{(n)}} \leftarrow \frac{{{{(f_k^{(n - 1)} - f_k^{(n - 2)})}^T}\left( {p_k^{(n)} - p_k^{(n - 1)}} \right)}}{{||f_k^{(n - 1)} - f_k^{(n - 2)}|{|^2}}}$
Step(4):$f_k^{(n)} \leftarrow f_k^{(n - 1)} - {\eta ^{(n)}}{g^{(n)}}$
对于所有像素点j: 如果满足fk(n)(j)<0,执行fk(n)(j) = 0
Step(5):利用f n及3D-OFM 算法重新估计Mi,k;反复执行此过程直至$||\mathop {{f^n}}\limits^ \to - \mathop {{f^{n - 1}}}\limits^ \to ||_2^2$,或者达到设定迭代次数。实验过程中,参数m 的取值设定为4,λ取值范围为1×101~1×103,根据不同实验而定。
2 结果 2.1 实验数据获取本文中,我们分别利用物理体模及真实临床数据进行算法测试。物理体模设计为静止的肺部仿真人体体模加直径约为3 cm的“运动组织”等效肿瘤。该肿瘤放置在左侧胸腔,与机械4D运动控制装置相连接。肿瘤的运动设定为幅值为13.4 m,沿轴向做正弦运动,周期为4 s。数据的采集利用瓦里安放疗设备获得,数据采集参数为:管电压120 kVp,旋转角度为360°,扫描时间大约为1 min,共获取投影数据约为620个,原始投影数据大小为1024×768,像素大小为0.388 mm×0.388 mm。 实验过程中,我们将投影数据降维为512×384,相应像素大小为0.776 mm×0.776 mm。利用标记点记录位置,我们将所有投影数据划分为8个相位。
病人数据我们采用http://www.openrtk.org/[16]网站共享的投影数据,扫描角度范围为360,总的投影个数为644,依据网站提供的投影数据相位信息,我们将投影划分为10个相位。
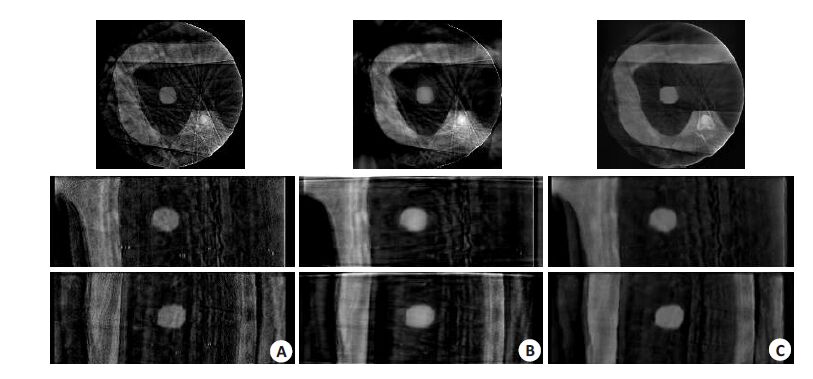
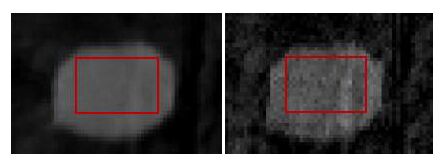
2.2 实验结果分析 2.2.1 物理体模重建结果分析图2 给出了某一呼吸相位的物理体模的重建结果,其中,从FDK 算法重建的图像我们可以看到,由于投影数据的缺失,重建图像中存在大量的伪影和噪声,很多解剖结构信息无法辨识( 2A)。ART-TV算法重建结果,可以看到条形伪影得到有效的抑制,但由于投影数据本身的数据不足,导致重建效果有限(图2B)。而本文提出算法的重建结果,可以明显的看出,相对左侧图像,右侧图像噪声和伪影较少,结构清晰,图像质量得到很大提升(图2C)。进一步的,表1 给出了以上FDK及本文提出重建算法在不同呼吸相位下肿瘤均质区域(图3)标准差计算值,其中所选取得区域为图3所示的区域,大小为20×16个像素。 从计算结果可以看出,本文提出的算法重建图像的标准差远低于FDK算法重建图像,进一步说明本文算法能够有效的抑制了图像噪声。
|
图2 某一呼吸相位物理体模重建结果 Fig.2 Physical phantom results of a selected phase. A: FDK reconstruction; B: ART-TV reconstruction; C: Reconstructions using the proposed algorithm. |
| 表1 不同重建算法肿瘤均质区域的标准差对比 Table 1 Standard deviations of the homogeneous regions for different reconstruction methods |
|
图3 用于计算噪声水平的均质区域,红色方框表示选定区域 Fig.3 A homogenous region (boxed) used to evaluate the noise. |
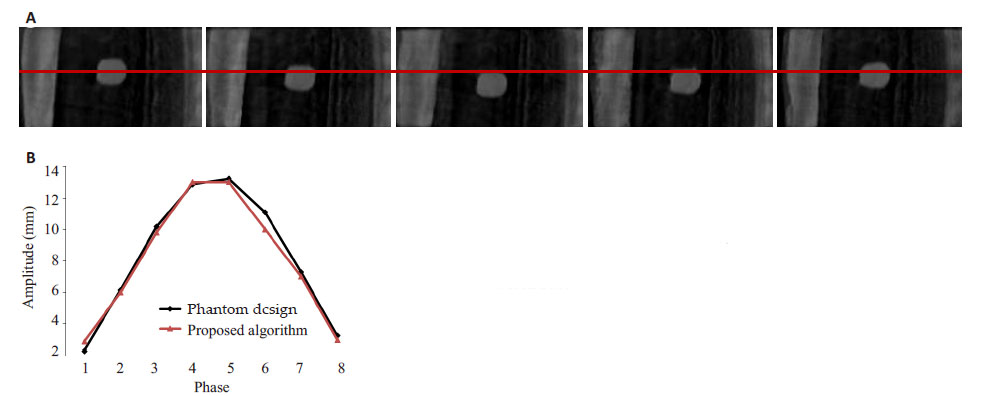
图4 给出了对应于5个呼吸相位的本文算法重建结果的矢状面图像(图4A)以及相应的肿瘤运动轨迹图(图4B)。结果显示,本文算法能有很好的重建出运动肿瘤而不引入运动模糊或伪影,同时,对比于原始实验设计的肿瘤运动模型,本文算法能够准确的刻画肿瘤运动的轨迹。
|
图4 体模本文算法重建结果的矢状面图像(A)以及相应的肿瘤运动轨迹曲线图(B) Fig.4 Sagittal reconstructed images of the physical phantom (A) and the corresponding tumor trajectory curves (B). |
图5 和图6 分别给出了病人数据5个呼吸相位的本文算法重建结果的冠状面和矢状面图像。图5和图6中,第1行为FDK算法重建图像,第2行为本文算法重建结果。可以明显的看出,FDK重建图像中伪影和噪声掩盖了许多图像的细节信息,同时使图像的对比度明显下降,肿瘤边界特征不明显。而本文算法重建图像,肺部细节结构信息明显,图像整体噪声水平较低,对比度较高,肿瘤边界相对明显。这对于后续的图像分析(如图像分割)及肿瘤运动轨迹提取都是极为有利的。
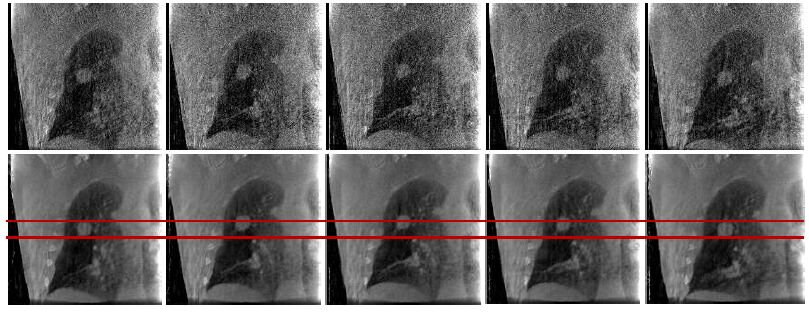
|
图5 对应于5个呼吸相位的本文算法重建结果的冠状面图像 Fig.5 Coronal reconstructed images of 5 selected phases. The first column shows the FDK reconstructions and the second column shows the reconstructions with the proposed algorithm. |
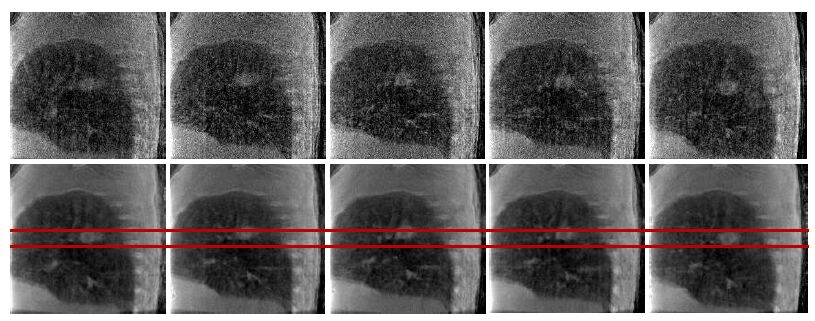
|
图6 对应于5个呼吸相位的本文算法重建结果的矢状面图像 Fig.6 Reconstructed sagittal images of 5 selected phases. The first column shows the FDK reconstructions and the second shows the reconstructions with the proposed algorithm. |
常规迭代重建算法[17, 18]数据保真项的设计一般只涉及当前呼吸相位投影数据而忽略了不同相位图像之间的相关性。本文中,我们充分利用4D-CBCT 中不同呼吸相位图像间的相关特性,通过引入运动补偿算子,将不同相位的图像关联在一起,进而构建当前投影数据与其他相位图像的关系式,并将改进后的成像模型融入代价函数保真项的设计中,构建基于多相位投影数据的压缩感知4D-CBCT重建模型。对模型的求解优化采用,GPBL算法实现。影响算法性能比较关键的一步为迭代重建过程中的运动估计,运动估计不足会造成重建图像的运动模糊的存在,运动估计过度则会造成重建图像出现伪影伪像。同时,重建过程中各参数的选择也会较大的影响重建结果,参数选择问题是一个公开的难优化的问题,在此我们不对重建参数做过多的讨论。本文算法中,我们引入全变分正则化的策略,一则为了抑制噪声及伪影,二则为了防止运动模糊产生,保持边缘特征。从实验结果来看,本文提出的算法能够有效的抑制重建图像中的噪声和伪影,提高重建图像的质量,同时准确的刻画肿瘤运动轨迹。
| [1] |
She J, Yang P, Hong Q, et al. Lung cancer in China: challenges and interventions[J]. Chest, 2013 Apr, 143(4): 1117-26. ( 1) 1)
|
| [2] |
Chang JY, Dong L, Liu H, et al. Image-guided radiation therapy for non-small cell lung cancer[J]. J Thorac Oncol, 2008, 3(2): 177-86. ( 1) 1)
|
| [3] |
Lewis SL, Patel P, Song H, et al. Image guided hypofractionated postprostatectomy intensity modulated radiation therapy for prostate cancer[J]. Int J Radiat Oncol Biol Phys, 2016, 94(3): 605-11. ( 1) 1)
|
| [4] |
Elsayad K, Kriz J, Reinartz G, et al. Cone-beam CT-guided radiotherapy in the management of lung cancer: Diagnostic and therapeutic value[J]. Strahlenther Onkol, 2016, 192(2): 83-91. ( 1) 1)
|
| [5] |
Han X, Pearson E, Pelizzari C, et al. Algorithm-enabled exploration of image-quality potential of cone-beam CT in image-guided radiation therapy[J]. Phys Med Biol, 2015, 60(12): 4601-33. ( 1) 1)
|
| [6] |
Korreman S, Persson G, Nygaard D, et al. Respiration-correlated image guidance is the most important radiotherapy motion management strategy for most lung cancer patients[J]. Int J Radiat Oncol Biol Phys, 2012, 83(4): 1338-43. ( 1) 1)
|
| [7] |
Kipritidis J, Hugo G, Weiss E, et al. Measuring interfraction and intrafraction lung function changes during radiation therapy using four-dimensional cone beam CT ventilation imaging[J]. Med Phys, 2015, 42(3): 1255-67. ( 1) 1)
|
| [8] |
Sonke J, Wolthaus J, Rossi M, et al. Four dimensional cone beam CT for verification of radiotherapy for lung cancer[J]. Lung Cancer, 2005, 49(2): S52. ( 1) 1)
|
| [9] |
Brehm M, Berkus T, Oehlhafen M, et al. Motion-Compensated 4D Cone-Beam computed tomography[C]//2011 IEEE NUCLEAR SCIENCE SYMPOSIUM AND MEDICAL IMAGING CONFERENCE (NSS/MIC), 2011: 3986-93. ( 1) 1)
|
| [10] |
Brehm M, Paysan P, Oelhafen M, et al. Artifact-resistant motion estimation with a patient-specific artifact model for motioncompensated cone-beam CT[J]. Med Phys, 2013, 40(10): 101913. ( 1) 1)
|
| [11] |
Sidky EY, Pan X. Image Reconstruction in circular cone-beam computed tomography by constrained, total-variation minimization [J]. Phys Med Biol, 2008, 53(17): 4777-807. ( 2) 2)
|
| [12] |
Zhang H, Ouyang L, Huang J, et al. Few-view cone-beam CT Reconstruction with deformed prior image[J]. Med Phys, 2014, 41 (12): 121905. ( 1) 1)
|
| [13] |
Leng S, Tang J, Zambelli J, et al. High temporal resolution and streak-free four-dimensional cone-beam computed tomography[J]. Phys Med Biol, 2008, 53(20): 5653-73. ( 2) 2)
|
| [14] |
Zhang Y, Tong X, Yang T, et al. Multi-model estimation based moving object detection for aerial video[J]. Sensors (Basel), 2015, 15(4): 8214-31. ( 1) 1)
|
| [15] |
Bonettini S, Prato M. A new general framework for gradient projection methods[J]. Eprint Arxiv, 2014, 1406, 6601. ( 1) 1)
|
| [16] |
Rit S, Oliva1 Vila M, Brousmiche S, et al. The Reconstruction Toolkit (RTK), an open-source cone-beam CT reconstruction toolkit based on the Insight Toolkit (ITK)[C]. J Physics: Conf Series, 2014, 489, 012079. ( 1) 1)
|
| [17] |
Alasti H, Cho YB, Vandermeer AD, et al. A novel four-dimensional radiotherapy method for lung cancer: imaging, treatment planning and delivery[J]. Phys Med Biol, 2006, 51(12): 3251-67. ( 1) 1)
|
| [18] |
Sonke J, Zijp L. Remeijer P and Herk M. respiratory correlated cone beam CT[J]. Med Phys, 2005, 32(4): 1176-86. ( 1) 1)
|
 2016, Vol. 36
2016, Vol. 36
